Что значит плоскости пересекаются

Взаимное расположение плоскостей: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке

Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей

Пусть две плоскости и заданы общими уравнениями и .

Вопрос об определении угла между ними сводится к определению угла между векторами нормалей к ним

и .

Из определения скалярного произведения и из выражения в координатах длин векторов и и их скалярного произведения получим

Условие параллельности плоскостей и эквивалентно условию коллинеарности векторов и и заключается в пропорциональности координат этих векторов:

.

Условие перпендикулярности плоскостей и может быть выражено равенством нулю скалярного произведения векторов нормалей к ним и :

.

Решение. Составим уравнения коэффициентов уравнений плоскостей:

Так как , то коэффициенты пропорциональны, следовательно данные две плоскости параллельны.

Пример 2. Установить, перпендикулярны ли плоскости, заданные уравнениями и .

Решение. Плоскости перпендикулярны в том случае, когда векторы и нормалей к ним перпендикулярны и удовлетворяют условию равенства нулю их скалярного произведения. Так как , то указанное условие выполнено и, значит, данные плоскости перпендикулярны.

Условие пересечения трёх плоскостей в одной точке, точка пересечения

Необходимым и достаточным условием того, что три плоскости имеют только одну общую точку (то есть, пересекаются в этой точке), является условие неравенства нулю определителя, составленного из коэффициентов уравнений:

Это условие совпадает с условием того, что система линейных уравнений имеет одно единственное решение (пройдя по ссылке можно увидеть иллюстрацию как раз на примере плоскостей).

Решение системы общих уравнений плоскостей (если оно существует и единственное) и даёт точку пересечения трёх плоскостей.

Пример 3. Установить, пересекаются ли три плоскости в одной точке, если пересекаются, найти точку пересечения. Плоскости заданы уравнениями:

Решение. Сначала проверим, выполняется ли условие пересечения плоскостей в одной точке. Для этого установим, отличен ли от нуля определитель системы:

Определитель отличен от нуля, следовательно система уравнений имеет единственное решение, а, значит, три плоскости пересекаются в одной точке.

Для нахождения этой точки продолжим решать систему уравнений методом Крамера. Перенесём свободные члены в правые части уравнений:

Найдём определители при неизвестных:

Нетрудно заметить, что по формулам Крамера (определитель при неизвестной делить на определитель системы) все неизвестные оказались равными единице. Таким образом, получили точку пересечения трёх плоскостей:

Для проверки решения подобных задач целесообразно воспользоваться калькулятором, решающим системы уравнений методом Крамера.

Пример 4. Установить, пересекаются ли три плоскости в одной точке, если пересекаются, найти точку пересечения. Плоскости заданы уравнениями:

Решение. Проверим, пересекаются ли плоскости в одной точке. Для этого вычислим определитель системы:

Определитель равен нулю, следовательно, данные три плоскости не пересекаются в одной точке.

Для проверки решения подобных задач целесообразно воспользоваться калькулятором, решающим системы уравнений методом Крамера.

Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости

Пусть даны точка и плоскость . Тогда уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости, имеет вид

.

Решение. Подставляем в формулу, данную в теоретической сравке к этой главе, данные точки и другой плоскости. Получаем:

Последнее и есть искомое уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости.

Источник

Пересекающиеся плоскости

Плоскость — это одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Линия пересечения двух плоскостей — это прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

Содержание:

Понятие пересекающихся плоскостей

Определение. Плоскости, которые имеют хотя бы одну общую точку, называют пересекающимися.

Аксиома 5. Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

При этом если какая-либо точка принадлежит обеим плоскостям, то она принадлежит прямой . Плоскости и в этом случае являются пересекающимися по прямой (рис. 2.379).

Пример:

Дана плоскость . Доказать, что существует другая плоскость (3, пересекающая .

Решение:

Из условия задачи имеем:

1. Плоскость (дано) (рис. 2.380).

2. Нужно доказать, что существует другая плоскость , пересекающая .

Мы знаем, что на основании аксиомы 3 (аксиомы плоскости) три точки определяют единственную плоскость.

3. Возьмем точки А и В, принадлежащие плоскости , и точку С, не лежащую на прямой АВ и не принадлежащую (построение) (рис. 2.381).

4. Точки А, В и С не лежат на одной прямой. Через них можно провести плоскость , и притом только одну (3, аксиома 3).

5. Плоскости и имеют общую точку (1, 3, 4).

6. Плоскости и пересекаются по прямой АВ (5, аксиома 5) (рис. 2.382).

7. Мы доказали, что существует плоскость Р, пересекающая . (6)

Замечание. Если допустить, что точка С лежит на прямой АВ, то она будет лежать и в плоскости , что противоречит выбору точки С.

Двугранные углы

При пересечении плоскостей образуются двугранные углы.

Определение. Фигуру, образованную двумя полуплоскостями, исходящими из одной прямой, называют двугранным углом. Прямую называют ребром, а полуплоскости — сторонами или гранями двугранного угла.

На рисунке 2.383 изображен двугранный угол с ребром АВ.

Этот угол можно обозначать двумя буквами, поставленными у его ребра (двугранный угол АВ). Но если при одном ребре лежит несколько двугранных углов, то каждый из них обозначают четырьмя буквами, из которых две средние стоят при ребре, одна крайняя — у одной грани, другая — у другой (рис. 2.384).

Определение. Если через произвольную точку ребра двугранного угла провести плоскость, перпендикулярную ребру, то в пересечении этой плоскости с двугранным углом образуется угол, который называют линейным углом двугранного угла.

На рисунке 2.385 изображен линейный угол АОВ двугранного угла АОСВ. Вершиной линейного угла служит точка О, лежащая на ребре ос двугранного угла, а сторонами — лучи граней, исходящие из точки о и перпендикулярные ребру двугранного угла.

Двугранный угол имеет бесконечное множество линейных углов (рис. 2.386).

Определение. Градусной мерой двугранного угла называют градусную меру любого из его линейных углов.

Определение. Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°).

Можно доказать следующее утверждение.

Теорема 1. Все линейные углы двугранного угла равны друг другу.

Для двугранных углов так же, как и для плоских, вводится понятие его градусной меры — величины.

Определение. Два двугранных угла называют равными, если они имеют одну и ту же градусную меру.

Если градусная мера одного из двугранных углов больше градусной меры другого, то говорят, что первый двугранный угол больше второго, а второй меньше первого. На рисунке 2.387 изображены три двугранных угла с общим ребром АВ. Двугранные углы CABD и DABE равны, так как их градусные меры равны 30°. Двугранный угол САВЕ больше двугранного угла CABD.

Подобно плоским углам, двугранные углы могут быть смежные, вертикальные и пр.

Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.

Все сказанное можно сформулировать в виде теорем.

Теорема 2. 1. Равным двугранным углам соответствуют равные линейные углы.

2. Большему двугранному углу соответствует больший линейный угол.

Верна и обратная теорема.

Теорема 3. 1. Равным линейным углам соответствуют равные двугранные углы.

2. Большему линейному углу соответствует больший двугранный угол.

Из теорем 2 и 3 легко получить три следствия.

Следствие 1. Прямому двугранному углу соответствует прямой линейный угол, и обратно.

Следствие 2. Все прямые двугранные углы равны, потому что у них равны линейные углы.

Следствие 3. Вертикальные двугранные углы равны.

Пример:

Из условия теоремы имеем:

1. PABQ и — два данных двугранных угла (рис. 2.388).

2. Вложим угол в угол АВ так, чтобы ребро совпало с ребром АВ, а грань — с гранью Р (построение) (рис. 2.389).

3. Если эти двугранные углы равны, то грань совпадает с Q; если же двугранные углы не равны, то грань займет некоторое положение, не совпадающее с Q, например положение (1, 2).

4. Возьмем на общем ребре какую-нибудь точку В и проведем через нее плоскость , перпендикулярную ребру АВ (построение) (рис. 2.390).

5. От пересечения этой плоскости с гранями двугранных углов получатся линейные углы.

Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол cbd; если же двугранные углы не совпадут (если, например, грань займет положение то у большего двугранного угла окажется больший линейный угол (именно ) (3, 4).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник

Когда две плоскости пересекаются друг с другом, что лучше всего описывает пересечение?

Когда две плоскости пересекаются, они образуют линию.

Тогда, может ли пересечение двух плоскостей быть точкой?

If две плоскости пересекаются, Они пересекаться в строке. Две плоскости это не пересекаться называются параллельными. Линия и самолет пересекаться в одном точка. Линия и плоскость не пересекаются.

Учитывая это, почему две плоскости пересекаются на одной линии? Если векторы нормалей параллельны, два самолета либо идентичны, либо параллельны. Если векторы нормалей не параллельны, то два самолета встретиться и сделать линия of пересечение, который представляет собой набор точек, которые находятся на обоих самолеты.

Что происходит, когда пересекаются 3 плоскости?

Сформируйте систему с уравнениями самолеты и подсчитайте ранги. Каждая плоскость разрезает две другие по прямой, и они образуют призматическую поверхность. Второй и третий самолеты совпадают, и первый их режет, поэтому три плоскости пересекаются в строке.

Сколько точек в линии?

Что представляет собой фигура из 3-х плоскостей, которые встречаются в точке?

2. Каждый план пересекается точка. 3. Второй и третьи самолеты совпадают, и первый их режет, поэтому три самолета пересекаются по прямой.

Что есть особенный момент?

Две отдельные точки определить ровно одну строку. Если два пунктов линии лежат на плоскости, вся линия лежит на плоскости. Именно это свойство делает самолет «плоским». Два отчетливый линии пересекаются не более чем в одном точка; два отчетливый плоскости пересекаются не более чем по одной линии.

Что является пересечением двух различных непараллельных прямых?

Сколько точек в линии?

Три пунктов, линия (прямой линия) можно рассматривать как связное множество бесконечно много очков. Он распространяется бесконечно далеко в двух противоположных направлениях. А линия имеет бесконечную длину, нулевую ширину и нулевую высоту.

Как вы думаете, как выглядит пересечение двух плоскостей?

Очевидно, что пересечение двух плоскостей ЛИНИЯ. В самолет, три точки Он коллинеарен. Если два из точек Он на одной линии, разве они не линейны?

Две линии пересекаются когда они пересекаются. Они образуют вертикально противоположные углы, о которых мы узнаем позже. Точка, где линии пересекаются is под названием точка пересечение. Если полученные углы являются прямыми, линий Он под названием перпендикуляр линий.

Компланарны ли параллельные линии?

Две линии параллельные линии если они копланарный и не пересекаются. Линии которые не являются копланарный и не пересекаются, называются перекосом линий. Две плоскости, которые не пересекаются, называются параллельно самолеты.

Какое наименьшее количество различных точек может определять плоскость?

Каковы все точки между двумя заданными точками, включая две точки?

В самолете всего 3 точки?

Что такое постулат двух точек?

Компланарны ли три точки?

Копланарные точки Он три или больше пунктов которые все лежат в одной плоскости. Любой набор три очка в космосе копланарный. Набор из четырех пунктов может быть копланарный а может и нет копланарный.

Какое минимальное количество точек необходимо для определения двух различных плоскостей?

минимальное количество точек, необходимых для определения двух различных плоскостей является 4 пунктов.

Могут ли три плоскости пересекаться в одной точке?

Две самолеты пересекаются, Треть пересекается наклонно и три пересекаются в точка. Каждая пара самолеты пересекаются в строке. В три линии не компланарны и не параллельны, а три линий пересекаться на точка где три самолета делать.

Когда две плоскости пересекаются, их пересечение всегда происходит ровно в одной точке?

Постулат: если две плоскости пересекаются, затем их пересечение это линия. Смысл Q лежит на прямой m и прямой l. Постулат: если два линий пересекаться, затем их пересечение is ровно один балл.

Сколько точек находится на пересечении двух различных линий?

Что такое перпендикулярная линия?

Важно знать о параллельные линии потому что вы собираетесь использовать это через все части геометрии. Технически параллельные линии два копланарный это означает, что они находятся в одной плоскости или находятся в одной плоскости, которая никогда не пересекается. И вы можете определить параллельные линии с одинаковым количеством стрелок.

Что является пересечением двух различных непараллельных прямых?

Находятся ли 4 точки в одной плоскости?

4 балов Он копланарный если объем, созданный пунктов равно 0. Если любые три пунктов определить самолет, затем дополнительные пунктов можно проверить для компланарность путем измерения расстояния до пунктов от плоскости, если расстояние равно 0, то точка is копланарный.

Как найти линию пересечения?

Как найти линию пересечения?

Почему две плоскости пересекаются на одной линии?

Если векторы нормалей параллельны, два самолета либо идентичны, либо параллельны. Если векторы нормалей не параллельны, то два самолета встретиться и сделать линия of пересечение, который представляет собой набор точек, которые находятся на обоих самолеты.

Сколько линий определяется двумя точками?

Поскольку мы дали две точки. И мы знаем определение линии, в котором говорится, что «линия образована две точки и его можно удлинить с обеих сторон ». Итак, От две точки, должна быть 1 строка. Следовательно, одна строка определяется двумя точками.

Что такое пересечение двух линий?

Теперь, где две линии крест называется их точкой пересечение. Конечно, эта точка имеет координаты (x, y). Это одна и та же точка для линии 1 и для линии 2. Итак, в точке пересечение координаты (x, y) для строки 1 равны координатам (x, y) для строки 2.

Источник

Пересекающиеся плоскости

Две плоскости пересекаются по прямой линии, для построения которой достаточно определить или две общие для плос­костей точки, или одну точку и направление линии пересечения.

Рассмотрим задачи на построение проекций линии пересечения плоскостей и их положения относительно плоскостей проекций.

1. Если плоскости заданы следами и следы пересекаются в пределах чертежа (рис. 4.14а), то две точки линии пересечения определяются на пересечении одноимённых следов. Точка 1 – пересечение горизонтальных следов, точка 2 – пересечение фронтальных следов. Линия l (l₁ l₂) – линия пересечения плос­костей l и å.

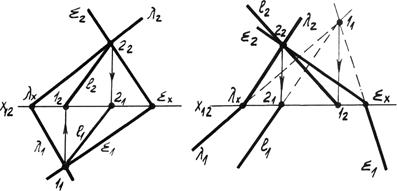
Рис. 4.14а. Плоскости заданы следами

2. Один из частных случаев пересечения плоскостей, когда одна из них является проецирующей плоскостью (рис. 4.14б).

Задача сводится к определению второй проекции линии, принадлежащей и проецирующей плоскости, и плоскости общего положения.

Определяем точки пересечения соответствующего следа проецирующей плоскости с плоскостью общего положения (точки 1 и 2). По линиям связи определяем вторую проекцию. Затем необходимо определить видимость отсеков плоскости общего положения относительно линии пересечения.

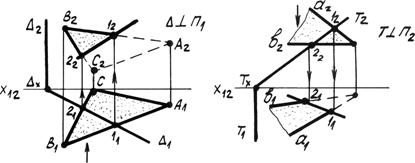
Рис. 4.14б. Одна из пересекающихся плоскостей – проецирующая

3. В некоторых случаях линия пересечения плоскостей является линией частного положения (рис. 4.14в).

Рассмотрим задачи на пересечение плоскостей по горизонтали. В первой задаче одна из плоскостей l является горизонтальной плоскостью уровня, поэтому фронтальная линия проекции пересечения h₂ совпадает со следом этой плоскости и является горизонталью. Горизонтальная проекция определяется по точке 1 пересечения следов и направлению h₁ || l₁.

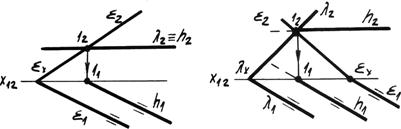Рис. 4.14в. Пересечение плоскостей по линиям частного положения

В примере 2 горизонтальные следы плоскостей общего положения параллельны (l₁ || å₁). Следовательно, горизонтальная проекция линии пересечения плоскостей будет параллельна им (h₁ || l₁ || å₁), а фронтальная проекция будет проходить через точку 1 пересечения фронтальных следов.

Аналогичны случаи пересечения плоскостей по фронтали. Существуют другие частные случаи пересечения плоскостей, когда линией пересечения являются проецирующие прямые.

4. Общий случай пересечения плоскостей, когда в пределах чертежа сразу не определяются общие для данных плоскостей точки. Для решения такой задачи используются вспомогательные секущие плоскости обычно частного положения – или плоскости уровня, или проецирующие.

Рассмотрим пример на рис. 4.15.

Даны две плоскости, заданные параллельными прямыми (а || b) и треугольником АВС. Для определения двух общих точек данных плоскостей решаем задачу по следующему алгоритму:

1. Вводим первую вспомогательную горизонтальную плоскость уровня å.

3. Определяем точку пересечения линии пересечения. Точка I – общая для данных плоскостей.

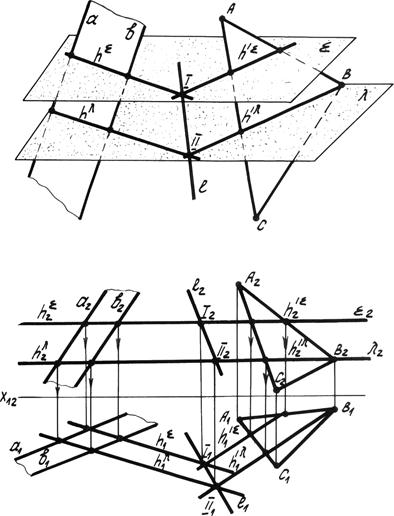Рис. 4.15. Общий случай пересечения плоскостей

4. Для определения ещё одной общей точки вводим вторую вспомогательную секущую плоскость уровня l. Выполним те же построения и определим вторую общую точку II.

5. Соединяем получившиеся точки I и II, которые определяют линию пересечения плоскостей l (l₁, l₂).

При решении некоторых задач удобнее использовать вспомогательные проецирующие плоскости.

Источник