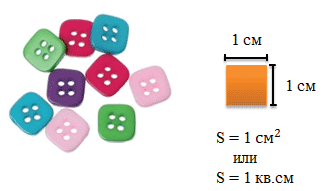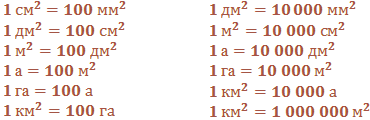Что значит площадь в математике
Что такое площадь в математике? Единицы площади
Есть проблемы с элементарной геометрией? Эта статья поможет вам решить одну из них. Здесь вы узнаете о том, что такое площадь в математике, об единицах ее измерения и других важных аспектах этой темы. Разбор некоторых конкретных примеров даст вам возможность глубже изучить вопрос.
Что такое площадь в математике?
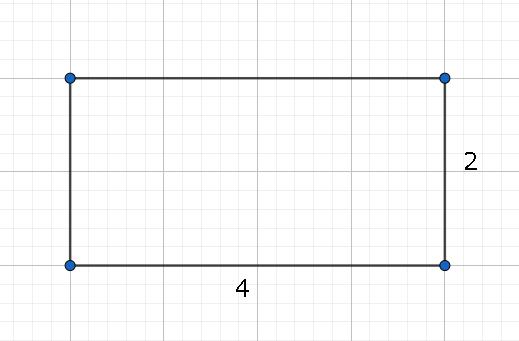
Площади фигур в математики вычисляются разными путями, зависимо от их формы. Например, в случае с прямоугольником необходимо найти произведение его высоты и ширины. Посмотрим на рисунок.
Проверить его можно вручную подсчитав количество больших квадратиков внутри прямоугольника. Подобной задачи достаточно для того чтобы объяснить, что такое площадь в математике. Но в этой теме есть еще и другие важные нюансы.
Единица измерения площади в математике
Измеряется площадь в квадратных единицах. То есть ее можно определить как некоторое количество четырехугольников, чьи стороны равны 1. При этом если поменять местами значения длины и высоты, конечный результат не изменится.
Примечание! Все величины должны быть в одинаковых единицах измерения.
Допустим, что данные заданы в сантиметрах. Как тогда правильно обозначить это на бумаге?
Вместо того чтобы писать «восемь квадратных сантиметров», можно использовать запись вида «8 см 2 «. Достаточно просто возвести сокращенную форму меры во вторую степень.
Перевод величин
У студента или ученика может возникнуть потребность перевести значение из одних единиц измерения в другие. Существует только один верный способ это сделать. Правда, для этого необходимо вспомнить, как правильно переводить одни единицы измерения в другие.
Другие фигуры
К сожалению, для нахождения площади не всегда достаточно перемножить два числа. Ситуации бывают разные. Рабочая формула для каждой из них будет видоизменяться из раза в раз. Ниже приведены наиболее часто встречаемые вариации фигур.
Пример
Теперь вы знаете, что такое площадь в математике. Основной теоретический материал усвоен, и можно переходить к практике. Для закрепления решим конкретную задачу.
Условие. Имеется квадрат со стороной 3 сантиметра и круг с радиусом такой же длины. Найдите, чья площадь больше и на сколько.
Решение. Для начала произведем вычисления для каждой из фигур по отдельности:
А вот площадь круга вычисляется уже по другой формуле. Для ее нахождения необходимо вспомнить значение ∏:
По результатам видим, что площадь круга в несколько раз больше. Осталось лишь посчитать на сколько. Для этого найдем разницу двух чисел.
Обычно, решая такие задачи, человек должен сводить все к готовым формулам. Затем уже искать неизвестные, выражать величины одну через другую и использовать смекалку.
Площадь
Что такое площадь
Понятие площади фигур рассматривается одним из разделов математики — конкретно, геометрией. Результат решения задач с нахождением площади геометрических фигур может использоваться для решения математических задач, в быту, в производстве.
Площадь фигуры — численная характеристика, которая передает информацию о размере геометрической фигуры.
Фигура, в математическом мире определяемая как множество точек на плоскости, должна быть ограничена со всех сторон, чтобы иметь понятие площади. Если фигура располагается на одной плоскости, она не имеет объема, а только площадь.
В самом простом случае, площадь фигуры можно посчитать по количеству клеток, которые она занимает. Подобным способом можно легко посчитать площадь квадрата, прямоугольника или прямоугольного равнобедренного треугольника.
Площадь в геометрии обозначается знаком S, от английского square — площадь.
Как математическая характеристика, площадь имеет четыре характеристики:
Единицы измерения площади
Площадь фигуры может измеряться в разных единицах в зависимости от поверхности, на которой располагается. Основной системой измерения считается Международная система единиц СИ.
Площадь измеряется в единицах измерения в квадрате:
В Древней Руси употребляли такие величины, как квадратная верста, десятина, квадратный сажень.
В античных источниках единицей измерения площади были актус, арура, центурия, югер.
Формула нахождения площади в математике
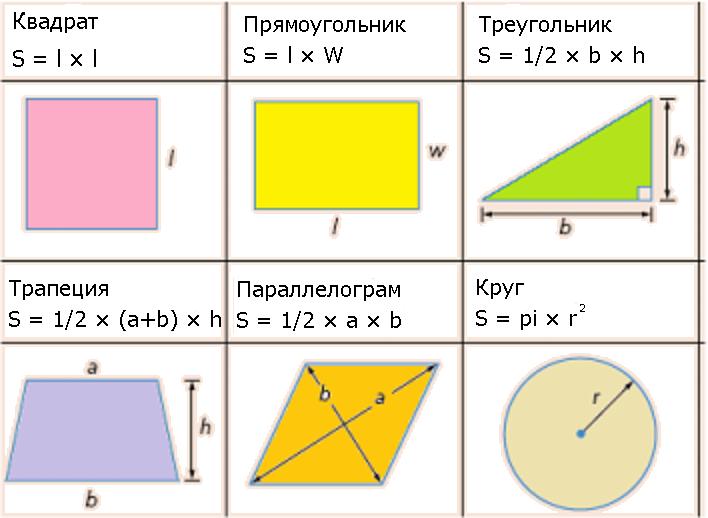
Существует множество формул нахождения площади простых геометрических фигур, которые зависят, в основном, от количества углов, сторон и их соотношений.
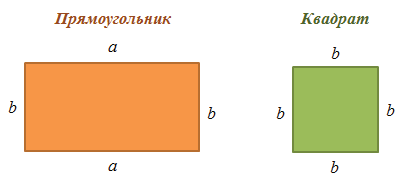
Площадь прямоугольника
Прямоугольником является геометрическая фигура, все углы которой равны 90°. При этом таких углов должно быть, как минимум три, а четвертый будет равен 90° в силу закона о сумме углов четырехугольника в евклидовой геометрии.
Вычисление площади прямоугольника будет происходить через умножение сторон:
где a и b являются сторонами прямоугольника.
Площадь квадрата
Квадратом является прямоугольник с равными сторонами. Все его углы равны 90°. Площадь квадрата можно найти сразу двумя способами:
По длине стороны:
Через диагонали:
где a — длина сторон квадрата;
d — длина диагоналей квадрата.
Площадь круга
Кругом является часть плоскости, которая лежит внутри окружности. Круг не имеет ни одного угла, а точки его окружности находятся на равном удалении от центра.
Площадь круга можно найти двумя способами:
Через радиус:
где π — постоянная Пи, равна 3,14.
Радиус, упоминаемый в формуле, является линией или отрезком, соединяющим центр и любую из точек окружности.
Через диаметр:
где π — постоянная Пи, равна 3,14.
Диаметр является отрезком, соединяющим две точки окружности и проходящим через центр. Он включает в себя два противоположно направленных радиуса.
Площадь эллипса
Эллипс является частным случаем окружности. Он, так же, как и круг, не имеет ни одного угла, но при этом точки окружности находятся на разном удалении от центра.
Найти площадь эллипса можно только одним способом: через произведение длин большой и малой полуосей эллипса и числа пи.
Площадь эллипса находится через произведение длин большой и малой полуосей эллипса и числа пи:
Площадь параллелограмма
Параллелограмм является геометрической фигурой с 4 углами и 4 сторонами, однако он отличается от прямоугольника по строению. Его противолежащие стороны попарно параллельны, а углы равны зеркально противолежащим.
Частными случаями параллелограмма являются квадрат, прямоугольник и ромб.
Найти площадь параллелограмма можно тремя способами:
Через сторону и высоту:
где a — сторона, к которой проведена высота,
h — высота непосредственно.
Через две стороны и величину угла между ними:
Через диагонали и угол между ними:
S = 1 2 × d 1 × d 2 × sin y
где d 1 и d 2 — это диагонали параллелограмма,
y — угол между ними.
Площадь ромба
Ромб, как частный случай параллелограмма, имеет те же свойства, кроме того, что все его стороны равны.
Площадь ромба также можно найти тремя способами:
По длине стороны и высоте:
Формула площади ромба по стороне и высоте выглядит так же, как и площадь параллелограмма по таким же характеристикам, с условием, что все высоты ромба будут равны:
По длине стороны и углу:
Формула площади ромба через длину сторон и углу между ними похожа на соответствующую формулу площади параллелограмма с условием того, что стороны равны, а значит, их перемножение можно заменить квадратом величины стороны:
По длине его диагоналей:
Площадь трапеции
Трапеция отличается от всех предыдущих фигур тем, что только две ее стороны, боковые, могут быть равны между собой. При этом они не параллельны. Две другие стороны параллельны, но не равны. Сумма углов трапеции равна 360°.
Площадь трапеции можно найти двумя способами:
По формуле Герона:
По длине основ и высоте:
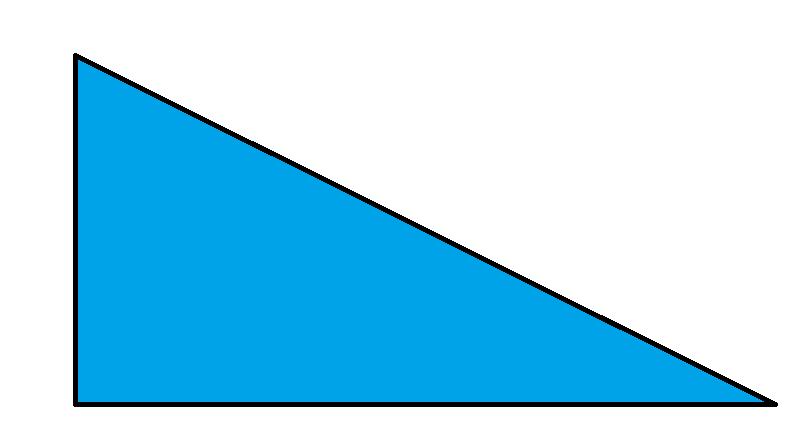
Площадь треугольника
Треугольник является геометрической фигурой с тремя сторонами и суммой углов, равной 180°. По величине углов треугольники делятся на острые, тупые и прямоугольные. По числу равных сторон треугольники делятся на разносторонние, равносторонние и равнобедренные.
Площадь треугольника можно найти множеством способов:
По гипотенузе и острому углу:
a — любой из прилежащих острых углов.
Через сторону и высоту:
Через три стороны:
где р — полупериметр.
Через две стороны и угол между ними:
S = 1 2 × a × b × sin y
Через три стороны и радиус описанной окружности:
Через три стороны и радиус вписанной окружности:
где р — полупериметр.
Пояснения на примерах
Стены класса равны 7 и 5 метрам. Чему будет равна площадь пола в данной комнате?
Решение: S = 7 × 5 = 35
Ткань летучего змея порвалась. Вася решил сделать новую форму. Он посчитал, что длина жердей летучего змея равна 15 и 23 см. Форму какой площади нужно взять Васе с учетом того, что для припусков для пришивания нужно взять еще 2 см?
Равнобедренный треугольник имеет основание 4 дм и высоту 7 дм. Сколько будет его площадь?
Площадь
Рассмотрим фигуру ниже:
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.
Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.
В математике для нахождения площади геометрических фигур используют специальные формулы, в которых площадь обозначается заглавной латинской буквой « S ».
Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата, равна 1 м, то его площадь равна 1 квадратному метру ( 1 м 2 ); если длина его стороны равна 1 см, то его площадь равна 1 квадратному сантиметру ( 1 см 2 ).
Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.
Как перевести квадратные единицы
Рассмотрим квадрат со стороной 1 см.
S = 1 см · 1 см = 1см 2
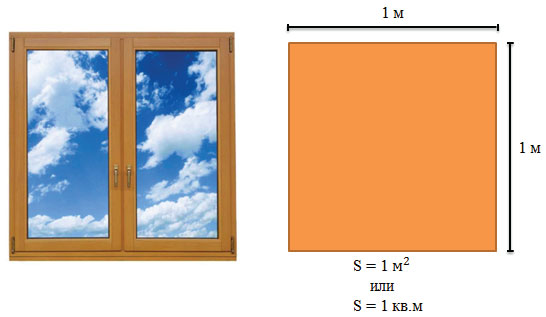
Рассмотрим квадрат со стороной 1 м.
S = 1 м · 1 м = 1 м 2
Известно, что: 1 м = 100 см
1 м 2 = 1 м · 1 м = 100 см · 100 см = 10 000 см 2
Увеличим сторону квадрата равную 1 м в 10 раз. Получим квадрат со
стороной 10 м.
Площадь такого квадрата называют ар или сотка.
S = 10 м · 10 м = 100 м 2
В одном аре — сто квадратных метров.
Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».
1 ар (сотка) = 100 м 2
Значит: 1 ар (сотка) = 100 м 2 = 100 · 10 000 см 2 = 1 000 000 см 2
Увеличим сторону квадрата равную 10 м в 10 раз. Получим квадрат со
стороной 100 м.
Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование проговаривается полностью.
Выразим гектар в квадратных метрах.
1 га = 100 м · 100 м = 10 000 м 2
Теперь определим, сколько в одном гектаре аров.
Значит: 10 000 м 2 : 100 м 2 = 100 (ар)
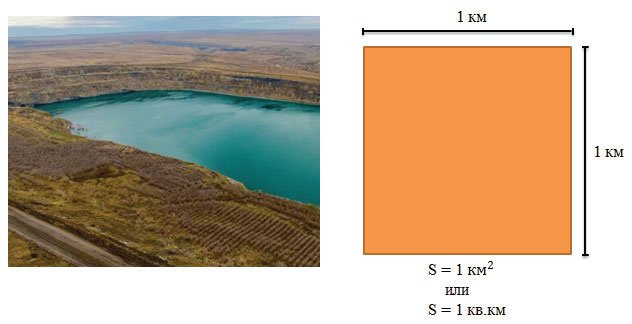
1 км 2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м 2
Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.
Таблица переводов квадратных единиц
Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.
Единицы измерения площадей. Свойства площадей
Измерение площадей
Для измерения площадей используют такие единицы измерения:
квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный километр
Квадратный сантиметр – это площадь квадрата со стороной в 1 см
Квадратный дециметр – это площадь квадрата со стороной в 1 дм
Квадратный метр – это площадь квадрата со стороной в 1 м
Для измерения больших площадей используют квадратный километр – это площадь квадрата, сторона которого равна 1 км
В квадратных километрах измеряют, например, площади городов (площадь Москвы 1091 км 2 )
Обозначают площадь заглавной буквой латинского алфавита S
Площади полей измеряют в гектарах (га).
Площади небольших участков земли измеряют в арах (а).
Соотношения между единицами измерения площадей
Если длина и ширина прямоугольника выражены, например, в метрах, то его площадь выражается в квадратных метрах.
Если длина и ширина прямоугольника измерены в разных единицах, то их надо выразить в одних единицах.
Свойства площадей
Поделись с друзьями в социальных сетях:
Площадь (математика, 5 класс) – что такое, правило обозначения и понятие
В школьном курсе математики 4-5 класса рассматривается понятие площади. Это значение часто встречается как в реальной жизни, где мы постоянно интересуемся площадью квартиры, так и при решении задач.
Определение понятия
Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.
Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.
Характеристики понятия
Площадь имеет несколько характеристик:
На практике площадь можно определять с помощью палетки или специального измерительного прибора – планиметра.
Площади простых фигур
Формула для определения площади зависит от фигуры. Обозначение площади, чаще всего, остается неизменным – это латинская заглавная буква “S”. Это не правило, просто одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах площадь могут обозначать другими буквами.
Рассмотрим наиболее популярные формулы определения площадей:
Рис. 1. Высота в произвольном треугольнике.
Предварительно нужно убедиться в том, что параметры фигуры находятся в одинаковых единицах измерения. Например, когда ширина прямоугольника представлена в миллиметрах, а длина в сантиметрах, следует перевести сантиметры в миллиметры и только потом использовать формулу.
Рис. 2. Площадь прямоугольника.
Что такое площадь квадрата? Это сторона фигуры, возведенная в квадрат. Потому что квадрат это прямоугольник, длина и ширина которого равны:
Если у квадрата одна сторона равняется 100 м, то его площадь равна одному гектару. Эту единицу используют, когда необходимо оценить размеры земной поверхности при распределении сельскохозяйственных угодий:
Площадь произвольной фигуры
Площадь сложной фигуры можно определить, просуммировав площади ее частей. Для этого нужно просто разделить произвольную геометрическую фигуру на простые составляющие так, чтобы можно было легко определить их квадратуры.
Рис. 3. Площадь сложной фигуры.
Что мы узнали?
Мы познакомились с понятием площади. Узнали, что для каждой фигуры есть свой метод определения площади. Важно, чтобы основные параметры фигуры были выражены в одних и тех же единицах.