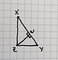Что значит пифагоровы штаны
Теорема Пифагора
Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².
Доказательство
Доказательство теоремы Пифагора, используя алгебру
Нужно доказать, что c² = a² + b²:
Это квадрат, в котором есть 4 одинаковых треугольника abc:
Что и требовалось доказать.
«Пифагоровы штаны на все стороны равны»
Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора
На этой фигуре c — гипотенуза, a и b — катеты.
Проведём перпендикулярную линию к гипотенузе (c):
Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).
Что и требовалось доказать.
Примеры
Задача 1
На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.
Подставить известные значения
Ответ: длина гипотенузы равна 5.
Задача 2
Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.
Подставить известные значения
Ответ: длина другой стороны треугольника равна 5.
Следствия из теоремы Пифагора
Это основные следствия теоремы:
Кто придумал теорему Пифагора
Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).
Узнайте также, что такое Теорема Виета и Аксиома.
Оригинальное доказательство теоремы Пифагора
Знаменитую теорему Пифагора — «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов» — знают все со школьной скамьи.
Ну, вы помните «Пифагоровы штаны», которые «во все стороны равны» — схематический рисунок, поясняющий теорему греческого ученого.
Здесь a и b — катеты, а с — гипотенуза:
Сейчас я вам расскажу об одном оригинальном доказательстве этой теоремы, о котором вы, возможно, не знали…
Но, сначала рассмотрим одну лемму — доказанное утверждение, которое полезно не само по себе, а для доказательства других утверждений (теорем).
Возьмем прямоугольный треугольник с вершинами X, Y и Z, где Z — прямой угол и опустим перпендикуляр с прямого угла Z на гипотенузу. Здесь W — точка, в которой высота пересекается с гипотенузой.
Эта линия (перпендикуляр) ZW разбивает треугольник на подобные копии самого себя.
Напомню, что подобными называются треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
В нашем примере образовавшиеся треугольники XWZ и YWZ подобны друг другу и также подобны исходному треугольнику XYZ.
Доказать это несложно.
Начнем с треугольника XWZ, обратите внимание, что ∠XWZ = 90, и поэтому ∠XZW = 180–90-∠X. Но 180–90-∠X — это именно то, что ∠Y, поэтому треугольник XWZ должен быть подобным (все углы равны) треугольнику XYZ. Такое же упражнение можно выполнить для треугольника YWZ.
Лемма доказана! В прямоугольном треугольнике высота (перпендикуляр), опущенная на гипотенузу, разбивает треугольник на два подобных, которые в свою очередь подобны исходному треугольнику.
Но, вернемся к нашим «Пифагоровым штанам»…
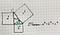
Опустим перпендикуляр на гипотенузу c. В результате у нас образовались два прямогульных треугольника внутри нашего прямоугольного треугольника. Обозначим эти треугольники (на картинке вверху зеленым цветом) буквами A и B, а исходный треугольник — буквой С.
Разумеется, площадь треугольника С равна сумме площадей треугольников A и B.
Теперь разобьем фигуру вверху («Пифагоровы штаны») на три фигурки-домика:
Как мы уже знаем из леммы, треугольники A, B и C подобны друг другу, поэтому и образовавшиеся фигурки-домики также подобны и являются масштабированными версиями друг друга.
Это означает, что соотношение площадей A и a², — это то же самое, что отношение площадей B и b², а также C и c².
Обозначим это соотношение площадей треугольника и квадрата в фигуре-домике буквой k.
Т.е. k — это некий коэффициент, связывающий площадь треугольника (крыши домика) с площадью квадрата под ним:
k = A / a² = B / b² = C / c²
Из этого следует, что площади треугольников можно выразить через площади квадратов под ними таким образом:
A = ka², B = kb², и C = kc²
Но, мы помним, что A+B = C, а значит, ka² + kb² = kc²
А это и есть доказательство теоремы Пифагора!
По материалам заметки Колина Фразера ( Colin Fraser)
Пифагоровы штаны
Пифаго́ровы штаны́ (школьн., устар.) — шуточное название одного из доказательств теоремы Пифагора.
История
В старых школьных учебниках приводилось доказательство теоремы через получение равенства суммы площадей квадратов, построенных на катетах прямоугольного треугольника, площади квадрата, построенного на гипотенузе этого треугольника. Построенные на сторонах треугольника и расходящиеся в разные стороны квадраты напоминали покрой мужских штанов, что породило шуточные четверостишия, например:
Пифагоровы штаны — На все стороны равны. Чтобы это доказать, Нужно снять и показать [1]
Пифагоровы штаны На все стороны равны, Потому что Пифагор Не ходил три дня во двор.
Пифагоровы штаны На все стороны равны, Число пуговиц известно Почему в штанах так тесно? Потому что хер велик — Отвечает ученик.
См. также
Примечания
Полезное
Смотреть что такое «Пифагоровы штаны» в других словарях:
Пифагоровы штаны — Жарг. шк. Шутл. Теорема Пифагора, устанавливающая соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
Пифагоровы штаны — Шуточное название теоремы Пифагора, возникшее в силу того, что построенные на сторонах прямоугольника и расходящиеся в разные стороны квадраты напоминают покрой штанов. Геометрию я любил… и на вступительном экзамене в университет получил даже от… … Фразеологический словарь русского литературного языка
пифагоровы штаны — Шутливое название теоремы Пифагора, устанавливающей соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника, что внешне на рисунках выглядит как покрой штанов … Словарь многих выражений
Пифагоровы штаны на все стороны равны — Число пуговиц известно. Почему же хую тесно? (грубо) о штанах и мужском половом органе. Пифагоровы штаны на все стороны равны. Чтобы это доказать, надо снять и показать 1) о теореме Пифагора; 2) о широких штанах … Живая речь. Словарь разговорных выражений
Пифагоровы штаны выдумать — Пиѳагоровы штаны (выдумать) иноск. о человѣкѣ даровитомъ. Ср. Это несомнѣнности мудрецъ. Въ древности онъ навѣрное выдумалъ бы пиѳагоровы штаны. Салтыковъ. Пестрыя письма. Пиѳагоровы штаны (геом.): въ прямоугольникѣ квадратъ гипотенузы… … Большой толково-фразеологический словарь Михельсона (оригинальная орфография)
Пифагоровы штаны во все стороны равны — Шутливое доказательство теоремы Пифагора; также в шутку о мешковатых брюках приятеля … Словарь народной фразеологии
штаны — сущ., мн., употр. сравн. часто Морфология: мн. что? штаны, (нет) чего? штанов, чему? штанам, (вижу) что? штаны, чем? штанами, о чём? о штанах 1. Штаны это предмет одежды, который имеет две короткие или длинные штанины и закрывает нижнюю часть… … Толковый словарь Дмитриева
Сокровище геометрии
Римский архитектор Витрувий особо выделял теорему Пифагора «из многочисленных открытий, оказавших услуги развитию человеческой жизни», и призывал относиться к ней с величайшим почтением. Было это ещё в I веке до н. э. На рубеже XVI–XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.
Пифагоровы штаны
Теорема Пифагора для случая равнобедренного прямоугольного треугольника
Теорема Пифагора едва ли не самая узнаваемая и, несомненно, самая знаменитая в истории математики. В геометрии она применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами a 2 + b 2 = c 2 невозможно. Однажды известный американский логик и популяризатор науки Рэймонд Смаллиан, желая подвести учеников к открытию теоремы Пифагора, начертил на доске прямоугольный треугольник и по квадрату на каждой его стороне и сказал: «Представьте, что эти квадраты сделаны из кованого золота и вам предлагают взять себе либо один большой квадрат, либо два маленьких. Что вы выберете?» Мнения разделились пополам, возникла оживлённая дискуссия. Каково же было удивление учеников, когда учитель объяснил им, что никакой разницы нет! Но стоит только потребовать, чтобы катеты были равны, — и утверждение теоремы станет явным (рис. 1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.
4000 лет спустя
Теперь, почти 4000 лет спустя, мы имеем дело с теоремой-рекордсменом по количеству всевозможных доказательств. Между прочим, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришёлся на вторую половину XIX — начало XX столетия. И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам. Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!
Самым древним из дошедших до нас доказательствам теоремы Пифагора около 2300 лет. Одно из них — строгое аксиоматическое — принадлежит древнегреческому математику Евклиду, жившему в IV–III веках до н. э. В I книге «Начал» теорема Пифагора значится как «Предложение 47». Самые наглядные и красивые доказательства построены на перекраивании «пифагоровых штанов». Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.
Вот какое изящное доказательство получается на основе чертежа из одного древнекитайского трактата (рис. 3), и сразу проясняется его связь с задачей об удвоении площади квадрата.
Иллюстрация к теореме Пифагора из «Трактата об измерительном шесте» (Китай, III век до н. э.) и реконструированное на его основе доказательство
Именно такое доказательство пытался объяснить своему младшему другу семилетний Гвидо, не по годам смышлёный герой новеллы английского писателя Олдоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность доказательства, поэтому приписал его. самому Пифагору. А вот главный герой фантастической повести Евгения Велтистова «Электроник — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данное Евклидом; правда, ошибочно назвал его простейшим, хотя на самом деле в современном издании «Начал» оно занимает полторы страницы!
Первый математик
Пифагора Самосского (570–495 годы до н. э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком. Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов. Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII–VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.
Другая важная заслуга Пифагора — основание славной школы математиков, которая более столетия определяла развитие этой науки в Древней Греции. С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.
Отделить достижения Пифагора от достижений его учеников невозможно: следуя обычаю, они приписывали собственные идеи и открытия своему Учителю. Никаких сочинений ранние пифагорейцы не оставили, все сведения они передавали друг другу устно. Так что 2500 лет спустя историкам не остаётся ничего иного, кроме как реконструировать утраченные знания по переложениям других, более поздних авторов. Отдадим должное грекам: они хоть и окружали имя Пифагора множеством легенд, однако не приписывали ему ничего такого, чего он не мог бы открыть или развить в теорию. И носящая его имя теорема не исключение.
Такое простое доказательство
Неизвестно, Пифагор сам обнаружил соотношение между длинами сторон в прямоугольном треугольнике или позаимствовал это знание. Античные авторы утверждали, что сам, и любили пересказывать легенду о том, как в честь своего открытия Пифагор принёс в жертву быка. Современные историки склонны считать, что он узнал о теореме, познакомившись с математикой вавилонян. Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Оно, конечно, не сохранилось. По одной из версий, Пифагор мог воспользоваться разработанным в его школе учением о пропорциях. На нём основывалась, в частности, теория подобия, на которую опираются рассуждения. Проведём в прямоугольном треугольнике с катетами a и b высоту к гипотенузе c. Получим три подобных треугольника, включая исходный. Их соответствующие стороны пропорциональны, a : с = m : a и b : c = n : b, откуда a 2 = c · m и b 2 = c · n. Тогда a 2 + b 2 = c · (m + n) = c 2 (рис. 4).
Чертёж к возможному доказательству Пифагора
Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, совсем простое: занимает всего-то несколько строк, не нужно ничего достраивать, перекраивать, вычислять. Неудивительно, что его не раз переоткрывали. Оно содержится, например, в «Практике геометрии» Леонардо Пизанского (1220), и его до сих пор приводят в учебниках.
Такое доказательство не противоречило представлениям пифагорейцев о соизмеримости: изначально они считали, что отношение длин любых двух отрезков, а значит, и площадей прямолинейных фигур, можно выразить с помощью натуральных чисел. Никакие другие числа они не рассматривали, не допускали даже дробей, заменив их отношениями 1 : 2, 2 : 3 и т. д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости диагонали квадрата и его стороны. Все попытки численно представить длину этой диагонали — у единичного квадрата она равна √2 — ни к чему не привели. Проще оказалось доказать, что задача неразрешима. На такой случай у математиков есть проверенный метод — доказательство от противного. Кстати, и его приписывают Пифагору.
Существование отношения, не выражаемого натуральными числами, положило конец многим представлениям пифагорейцев. Стало ясно, что известных им чисел недостаточно для решения даже несложных задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, её центральной проблемой. Сначала оно привело к разработке учения о несоизмеримых величинах — иррациональностях, а затем — и к расширению понятия числа. Иными словами, с него началась многовековая история исследования множества действительных чисел.
Мозаика Пифагора
«Мозаика Пифагора» и разбиение ан-Найризи трёх квадратов в доказательстве теоремы Пифагора
Если покрыть плоскость квадратами двух разных размеров, окружив каждый малый квадрат четырьмя большими, получится паркет «мозаика Пифагора». Такой рисунок издавна украшает каменные полы, напоминая о древних доказательствах теоремы Пифагора (отсюда его название). По-разному накладывая на паркет квадратную сетку, можно получить разбиения квадратов, построенных на сторонах прямоугольного треугольника, которые предлагались разными математиками. Например, если расположить сетку так, чтобы все её узлы совпали с правыми верхними вершинами малых квадратов, проявятся фрагменты чертежа к доказательству средневекового персидского математика ан-Найризи, которое он поместил в комментариях к «Началам» Евклида. Легко видеть, что сумма площадей большого и малого квадратов, исходных элементов паркета, равна площади одного квадрата наложенной на него сетки. А это означает, что указанное разбиение действительно пригодно для укладки паркета: соединяя в квадраты полученные многоугольники, как показано на рисунке, можно заполнить ими без пробелов и перекрытий всю плоскость.

Правильный паркет из квадратов и «мозаика Пифагора» на картинах голландских мастеров. Слева: П. де Хох. Хозяйка и служанка во внутреннем дворике. Около 1660 года. Справа: Я. Охтервелт. Бродячие музыканты в дверях богатого дома. 1665 год
* Паркет, или замощение, — разбиение плоскости многоугольниками (или пространства многогранниками) без пробелов и перекрытий.
Пифагоровы штаны
Смотреть что такое «Пифагоровы штаны» в других словарях:
Пифагоровы штаны — … Википедия
Пифагоровы штаны — Жарг. шк. Шутл. Теорема Пифагора, устанавливающая соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
пифагоровы штаны — Шутливое название теоремы Пифагора, устанавливающей соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника, что внешне на рисунках выглядит как покрой штанов … Словарь многих выражений
Пифагоровы штаны на все стороны равны — Число пуговиц известно. Почему же хую тесно? (грубо) о штанах и мужском половом органе. Пифагоровы штаны на все стороны равны. Чтобы это доказать, надо снять и показать 1) о теореме Пифагора; 2) о широких штанах … Живая речь. Словарь разговорных выражений
Пифагоровы штаны выдумать — Пиѳагоровы штаны (выдумать) иноск. о человѣкѣ даровитомъ. Ср. Это несомнѣнности мудрецъ. Въ древности онъ навѣрное выдумалъ бы пиѳагоровы штаны. Салтыковъ. Пестрыя письма. Пиѳагоровы штаны (геом.): въ прямоугольникѣ квадратъ гипотенузы… … Большой толково-фразеологический словарь Михельсона (оригинальная орфография)
Пифагоровы штаны во все стороны равны — Шутливое доказательство теоремы Пифагора; также в шутку о мешковатых брюках приятеля … Словарь народной фразеологии
штаны — сущ., мн., употр. сравн. часто Морфология: мн. что? штаны, (нет) чего? штанов, чему? штанам, (вижу) что? штаны, чем? штанами, о чём? о штанах 1. Штаны это предмет одежды, который имеет две короткие или длинные штанины и закрывает нижнюю часть… … Толковый словарь Дмитриева