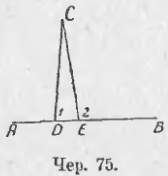Что значит перпендикулярно в геометрии в треугольнике

Что значит перпендикулярно в геометрии в треугольнике

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Перпендикуляр

Линия называется перпендикулярной плоскости, если она перпендикулярна каждой прямой в плоскости, которую она пересекает. Это определение зависит от определения перпендикулярности между линиями.

Две плоскости в пространстве называются перпендикулярными, если двугранный угол, под которым они встречаются, является прямым углом (90 градусов).

Содержание

Нога перпендикуляра [ править ]

Слово « стопа» часто используется в связи с перпендикулярами. Это использование проиллюстрировано на верхней диаграмме выше и в ее заголовке. Схема может быть в любой ориентации. Стопа не обязательно внизу.

Построение перпендикуляра [ править ]

Чтобы доказать, что точка PQ перпендикулярна AB, используйте теорему сравнения SSS для ‘и QPB’, чтобы заключить, что углы OPA ‘и OPB’ равны. Затем используйте теорему сравнения SAS для треугольников OPA ‘и OPB’, чтобы заключить, что углы POA и POB равны.

Теорема Пифагора может быть использована как основа методов построения прямых углов. Например, посчитав звенья, можно сделать три отрезка цепи с длинами в соотношении 3: 4: 5. Их можно выложить в виде треугольника, у которого будет прямой угол напротив его самой длинной стороны. Этот метод полезен для разбивки садов и полей, где размеры велики и не требуется большой точности. Цепи можно использовать повторно, когда это необходимо.

Относительно параллельных линий [ править ]

На рисунке справа все углы, заштрихованные оранжевым, конгруэнтны друг другу, а все углы, закрашенные зеленым, конгруэнтны друг другу, потому что вертикальные углы совпадают, а чередующиеся внутренние углы, образованные поперечными параллельными линиями сечения, равны конгруэнтный. Следовательно, если прямые a и b параллельны, любой из следующих выводов приводит ко всем остальным:

При вычислении расстояний [ править ]

Расстояние от точки до линии расстояние до ближайшей точки на этой линии. Это точка, в которой отрезок от нее до данной точки перпендикулярен прямой.

Точно так же расстояние от точки до кривой измеряется отрезком линии, перпендикулярным касательной к кривой в ближайшей точке кривой.

Перпендикулярная регрессия подгоняет линию к точкам данных путем минимизации суммы квадратов перпендикулярных расстояний от точек данных до линии.

График функций [ править ]

В кругах и других кониках [ править ]

Круги [ править ]

Теорема Фалеса утверждает, что две прямые, проходящие через одну и ту же точку на окружности, но проходящие через противоположные концы диаметра, перпендикулярны. Это эквивалентно тому, что любой диаметр окружности образует прямой угол в любой точке окружности, кроме двух конечных точек диаметра.

Эллипсы [ править ]

Параболы [ править ]

В параболе ось симметрии перпендикулярна каждой прямой прямой кишке, директрисе и касательной в точке, где ось пересекает параболу.

Гиперболы [ править ]

Поперечная ось из гиперболы перпендикулярна к сопряженной оси и к каждому директрисы.

Произведение расстояний по перпендикулярам от точки P на гиперболе или на ее сопряженной гиперболе до асимптот является константой, не зависящей от положения P.

В многоугольниках [ править ]

Треугольники [ править ]

Катеты прямоугольного треугольника перпендикулярны друг другу.

Эйлер линия из равнобедренного треугольника перпендикулярна к основанию треугольника.

Четырехугольники [ править ]

Линии в трех измерениях [ править ]

Источник

Математика

68. В п. 63 мы научились строить прямой угол. Так как две прямые, составляющие прямые углы, называются перпендикулярными друг другу (п. 60), то построение п. 63 можно выразить словами иначе: мы можем построить прямую, перпендикулярную к данной.

Мы теперь должны эту общую задачу разобрать подробнее и прежде всего разделим ее на две отдельных задачи:

1) Дана прямая и точка на ней, построить чрез данную точку перпендикуляр к данной прямой. (Можно ли и сколько?).

2) Дана прямая и точка вне ее; построить чрез данную точку перпендикуляр к данной прямой. (Можно ил и сколько?).

В скобках указаны те вопросы, которые должны быть выяснены при выполнении построений.

Здесь остается повторить то построение, какое было дано в п. 63.

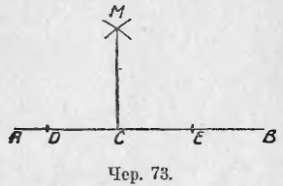
Пусть дана прямая AB и точка C на ней (чер. 73), построить чрез C перпендикуляр к AB.

От точки C откладываем по AB в разные стороны два произвольных, но равных отрезка CD = CE и затем, принимая последовательно точки D и E за центры, строим две окружности (или две дуги, достаточные для нахождения одной точки пересечения окружностей) одинаковыми радиусами, большими, чем отрезок CD. Точку пересечения M этих окружностей соединяем с C, тогда MC и есть искомый перпендикуляр, так как MC есть половина диагонали ромба, 3 вершины которого суть D, E и M.

Слово «перпендикуляр» пишут для сокращения знаком ⊥; мы построили

(CM перпендикуляр к AB).

Итак, выполнив это построение, мы можем признать, что чрез всякую точку, данную на прямой, можно построить к ней перпендикуляр (говорят иногда: восставить перпендикуляр к данной прямой). Остается еще вопрос: сколько?

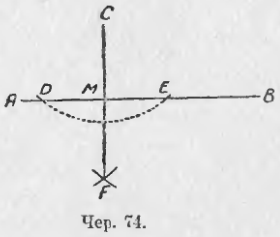
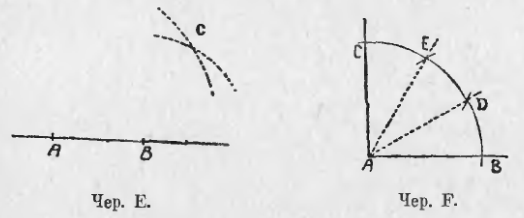
Пусть дана прямая AB и точка C вне ее (чер. 74); требуется чрез C построить перпендикуляр к AB.

Задача сводится к построению такого ромба, чтобы его одна вершина расположилась в точке C и одна его диагональ шла по прямой AB. Для построения такого ромба опишем, принимая C за центр, окружность (или дугу), выбрав ее радиус столь большим, чтобы эта окружность пересекалась с прямою AB; пусть она пересечет прямую AB в точках D и E. Тогда будут найдены еще две вершины ромба. Затем, принимая последовательно за центры точки D и E, построим два круга (или две дуги) тем же самым радиусом и найдем точку их пересечения, расположенную по другую сторону от прямой AB сравнительно с точкою C, пусть эта точка есть F. Тогда все 4 вершины ромба найдены; остается построить его диагональ CF, она, как мы знаем, и будет перпендикулярна к AB, т. е. CF ⊥ AB или CM ⊥ AB.

Стороны ромба DC, CE, EF и FD нет надобности строить.

Выполнив указанное построение, мы должны признать, что из всякой точки, данной вне прямой, мы можем построить перпендикуляр к данной прямой (говорят иногда: опустить перпендикуляр на данную прямую). Остается еще вопрос: сколько?

Для решения этого вопроса допустим, что чрез точку C (чер. 75) построено: 1) CD ⊥ AB и 2) CE ⊥ AB. Тогда ∠CDB или ∠1 и ∠CEB или ∠2 оба должны быть прямыми и, следов., равны между собою. Но ∠CEB есть внешний угол для ∆CDE, а мы знаем (п. 49), что внешний угол треугольника должен быть больше внутреннего с ним несмежного. Это противоречие показывает, что наше допущение не верно, т. е. Нельзя построить чрез точку C двух перпендикуляров к прямой AB. Итак:

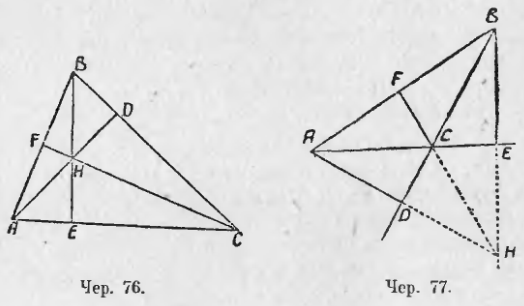
71. Построим какой-либо ∆ABC (чер. 76) и из каждой его вершины опустим перпендикуляр на противоположную сторону (здесь под именем сторона треугольника надо понимать бесконечную прямую). Каждый из этих перпендикуляров называется высотою треугольника. Следовательно, наша задача может быть выражена так: построить высоты треугольника. Если мы выполним построение перпендикуляров с возможною тщательностью, то в результате увидим, что по-видимому, все три высоты пересекаются в одной точке H, впоследствии мы выясним, что это свойство высот обязательно для всякого треугольника.

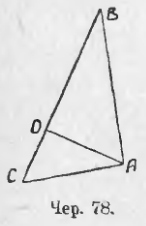
При построении высот может быть три случая: 1) все три высоты идут внутри треугольника (чер. 76); 2) две высоты BE и AD располагаются вне треугольника и общая точка H пересечения всех трех высот лежит вне треугольника (чер. 77) и 3) две высоты сливаются со сторонами треугольника (чер. 78), где BA ⊥ AC и CA ⊥ AB.

Нетрудно теперь различать и два остальных случая: случай, данный на чер. 76, имеет место тогда, когда все 3 угла в треугольнике острые, а случай, данный на чер. 77, имеет место тогда, когда один из внутренних углов (на чер. 77 ∠BCA) тупой.

Ясно также, что если в треугольнике один угол тупой (или > d), то сумма двух других углов должна быть 1-й признак. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого, то эти прямоугольные треугольники равны.

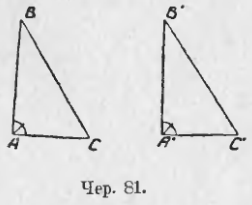
В самом деле это тот же самый признак, знакомый нам: если 2 стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, то треугольники равны. Теперь про углы не говорится потому, что между катетами расположены прямые углы, а они всегда равны (на чер. 81). ∠A = ∠A’, как прямые, и достаточно для равенства ∆ABC и ∆A’B’C’ знать, что AB = A’B’ и AC = A’C’).

2-й признак. Если катет и прилежащий острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то эти прямоугольные треугольники равны.

Это опять-таки знакомый нам признак: если 2 угла и сторона между ними одного треугольника соответственно равны двум углам и стороне между ними другого треугольника, то эти треугольники равны. Теперь про равенство углов, прилегающих к равным катетам у другого конца каждого, не говорится, так как эти углы прямые, а они всегда равны (на чер. 81, где ∠A и ∠A’ прямые, достаточно для равенства треугольников знать, что AB = A’B’ и ∠B = ∠B’).

Можно вместо прилежащих углов к катетам взять углы, противолежащие этим катетам: если ∠C = ∠C’, то и ∠B = ∠B’, так как ∠B + ∠C = d и ∠B’ + ∠C’ = d.

Признак равенства треугольников по трем равным сторонам здесь нет нужды применять: мы уже знаем, что для равенства прямоугольных треугольников достаточно знать равенство двух сторон, а именно двух катетов (1-й признак).

3-й признак. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого, то эти прямоугольные треугольники равны.

Этот признак является следствием общего признака: если 2 угла и сторона между ними одного треугольника соответственно равны двум углам и стороне между ними другого, то эти треугольники равны. В самом деле, пусть имеем 2 прямоугольных треугольника ABC и A’B’C’ (чер. 81), у которых BC = B’C’ и ∠С = ∠С’. Так как мы знаем, что ∠B + ∠C = d (сумма всех трех внутренних углов ∆ABC = 2d, но ∠A = d, следов., ∠B + ∠C = d) и ∠B’ + ∠C’ = d (ибо ∠A’ = d), а нам известно, что ∠C = ∠C’, то отсюда приходим к заключению, что ∠B = ∠B’ и тогда сторона BC и два прилегающих к ней угла ∠C и ∠B одного треугольника равны соответственно стороне B’C’ и двум прилегающим к ней углам другого ∠C’ и ∠B’, а мы знаем, что в этом случае ∆ABC = ∆A’B’C’.

4-й признак. Если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого, то такие прямоугольные треугольники равны.

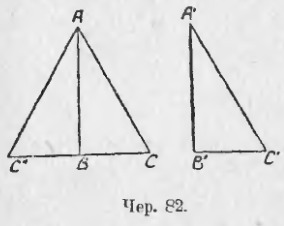
Этот признак удобнее всего выяснить следующим образом. Пусть имеем 2 прямоугольных треугольника ABC и A’B’C’ (чер. 82), причем ∠B = d и ∠B’ = d, у которых AC = A’C’ и AB = A’B’. Приложим ∆A’B’C’ и ∆ABC так, чтобы у них совпали равные катеты, т. е. A’B’ совпал бы с AB, и сами треугольники расположились бы по разные стороны от прямой AB, для этого иногда (напр., в случае, данном на чертеже) придется ∆A’B’C’ перевернуть другою стороною. Тогда сторона B’C’ должна пойти по такому направлению BC», чтобы ∠ABC» оказался прямым (ибо ∠B’ = d), а, следов., ∠CBC» оказался бы выпрямленным, т. е. Направление BC» должно быть продолжением стороны CB. Если точка C’ попадет в точку C», то, построив сторону AC», получим ∆ABC», равный ∆A’B’C’. Так как CBC» есть прямая линия, то получим еще ∆ACC», у которого сторона AC = AC», потому что AC» есть гипотенуза A’C’ треугольника A’B’C’, помещенного в положение ABC». Следовательно, ∆ACC» равнобедренный, а в таком случае углы при его основании равны, т. е. ∠C = ∠C», или ∠C = ∠C’. Оказалось, что у ∆ABC и ∠A’B’C’ имеется еще по равному острому углу, а в таком случае, на основании предыдущего признака, мы можем заключить, что ∆ABC = ∆A’B’C’.

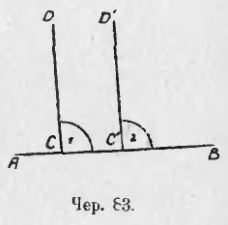
75. Пусть построено: 1) CD ⊥ AB и 2) C’D’ ⊥ AB (чер. 83); тогда, напр., ∠1 = ∠2, так как оба они прямые. Но эти углы суть соответственные при прямых CD и C’D’, пересеченных секущею AB, – следов., CD || C’D’.

Наоборот, пусть построено: 1) CD || C’D’ и 2) AB ⊥ CD (чер. 83); тогда AB должна пересечь и прямую C’D’ (п. 32, 1), напр. в точке C’. Легко увидим, что ∠2 = ∠1, так как эти углы соответственные при параллельных CD и C’D’ и секущей AB, но ∠1 = d, так как AB ⊥ CD, – следов., и ∠2 = d, т. е. AB ⊥ C’D’.
Поэтому имеем два заключения:

1) Два перпендикуляра к прямой параллельны.

2) Прямая, перпендикулярная к одной из параллельных, перпендикулярна и к другой.

76. Упражнения.

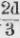
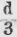
Третью часть прямого угла легко построить: каждый внутренний угол равностороннего треугольника = , а его половина = . Наиболее удобное расположение построения следующее: принимая вершину A прямого угла за центр (чер. F), строим произвольным радиусом окружность: затем, принимая за центры точки C и B – точки пересечения построенной окружности со сторонами прямого угла – строим тем же радиусом дуги, пересекающие построенную окружность в точках D и E. Тогда ∆AEB и ∆ACD равносторонние, и лучи AD и AE делят прямой ∠A на 3 равных части.

Источник

Геометрия. Урок 3. Треугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение треугольника

Треугольник – многоугольник с тремя сторонами и тремя углами.

Виды треугольников

Основные свойства треугольника:

Отрезки в треугольнике

Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.

Свойства биссектрис треугольника:

Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Свойства медиан треугольника:

Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.

Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.

Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.

Площадь треугольника

Площадь произвольного треугольника можно найти следующими способами:

Равнобедренный треугольник

Равнобедренным называется треугольник, у которого две стороны равны.

Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:

Равносторонний треугольник

Равносторонним называется треугольник, у которого все стороны и все углы равны.

Площадь равностороннего треугольника находится по формуле S = a 2 3 4

Высота равностороннего треугольника находится по формуле h = a 3 2

Прямоугольный треугольник

Свойства прямоугольного треугольника:

Теорема Пифагора

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с треугольниками

Источник