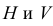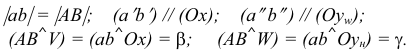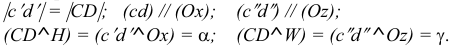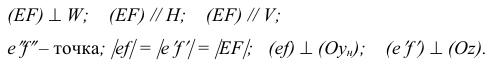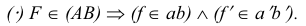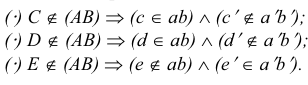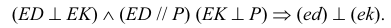Что значит пересекаются прямая и отрезок

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Геометрия – это наука, занимающаяся изучением геометрических фигур и отношений между ними.

Отрезок – это часть прямой, ограниченная точками, вместе с этими точками.

Концы отрезка – это точки, ограничивающие отрезок.

Теоретический материал для самостоятельного изучения.

«Геометрия – неотъемлемая часть мировой сокровищницы человеческой мысли», – однажды сказал российский математик Игорь Фёдорович Шарыгин.

С этих слов мы и начнём изучать новый раздел математики, который называется геометрия.

Геометрия – одна из древнейших наук, которая возникла из потребностей человека. Её название состоит из двух древнегреческих слов: гео – земля и метрео – измеряю, получается: «землю измеряю». Действительно, слово «геометрия» связано с измерениями, как на земельных участках, так и при строительстве зданий. Многие факты добывались опытным путем, поэтому геометрия не являлась точной наукой во времена своего зарождения.

Геометрические сведения стали доказываться только благодаря древнегреческому учёному Фалесу, который жил в VI веке до нашей эры.

Спустя некоторое время, уже в III веке до нашей эры, другой греческий учёный Евклид написал «Начала». Эта книга стала основой изучения геометрии на долгое время, а наука в честь учёного была названа евклидовой геометрией.

Сегодня геометрия – это наука, занимающаяся изучением геометрических фигур и отношений между ними.

В школе изучается два курса геометрии – планиметрия, в ней рассматриваются свойства фигур на плоскости, и стереометрия, в ней рассматриваются свойства фигур в пространстве.

В каждой науке есть свои термины, понятия, геометрия не исключение. В геометрии есть основные положения, которые принимаются в качестве исходных и носят название аксиом и основные понятия, определение которым не даётся, например, точка и прямая, но их свойства выражены в аксиомах. Это всё является фундаментом геометрии, на котором строятся другие понятия и доказываются теоремы.

Рассмотрим некоторые из аксиом.

1. Аксиомы принадлежности.

Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.

2. Аксиомы расположения.

Из трех точек на прямой одна и только одна лежит между двумя другими.

3. Аксиомы измерения.

Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

В целом аксиомы разделены на 5 групп, 3 из которых, частично, представлены вашему вниманию.

В 7 классе вы будете изучать планиметрию. Давайте перечислим некоторые понятия из этого раздела геометрии. Поговорим о точках, прямых, отрезках, вспомним, как они обозначаются.

Обычно прямую обозначают малой латинской буквой (например, a), а точки большими латинскими буквами, например, A.

Если на прямой отметить точки, например, A и B, то прямую в можно обозначить двумя заглавными буквами AB или BA.

Часть прямой, ограниченной точками, включая эти точки, называют отрезком. В нашем случае получаем отрезок AB или BA.

Точки, ограничивающие отрезок, называются концами отрезка. В нашем случае концами отрезка являются точки A и B.

Варианты взаимного расположения точек и прямой: точки могут лежать на прямой или не лежать на ней.

Например, точки A и B лежат на прямой a, точки C и D не лежат на прямой a. При этом в записи используют следующее обозначение:

Это можно прочитать таким образом: «точка A и B принадлежат прямой a (ϵ – знак принадлежности), также точки C и D не принадлежат прямой a (перечёркнутый знак принадлежности)».

При этом через точки А и В нельзя провести прямую, не совпадающую с прямой а, из этого делаем вывод, что через любые две точки можно провести только одну прямую.

Рассмотрим, как располагаются прямые на плоскости.

Прямые могут иметь только одну общую точку, тогда говорят, что прямые пересекаются или не иметь общих точек, тогда говорят, что прямые не пересекаются.

прямые пересекаются – прямые не пересекаются

Решим задачу. Построим с помощью линейки отрезок длиннее, чем она сама. Приём, который мы будем использовать, называется провешиванием прямой.

Рассмотрим, в чём он заключается. Для этого приложим к листу бумаги линейку и отметим три точки А, В, С, при этом, точка С пусть лежит между точками А и В. Далее передвинем линейку так, чтобы её конец оказался около точки С, отметим точку D. Все построенные точки А, В, С, D лежат на одной прямой. Теперь проведём отрезок АВ, потом отрезок ВD, в результате получим отрезок АD длиннее, чем линейка.

Для построения на местности отмечают две точки, например, А и В, ставят в них шесты (вехи), третий шест ставят в точку С так, чтобы её закрывали уже ранее поставленные шесты.

Так можно прокладывать линии высоковольтных передач, трассы и т. д.

Разбор заданий тренировочного модуля.

1. Сколько отрезков образуется при пересечении прямых на рисунке?

Посмотрите на рисунок. На нём изображены 4 пересекающиеся прямые, точки пересечения разбивают прямые на отрезки: прямая с разбивается на 3 отрезка АЕ, АВ, ЕВ. Аналогично все прямые разбиваются на 3 отрезка. В результате получаем, что каждая из четырёх прямых, разбивается точками пересечения на 3 отрезка, значит: 4 · 3 = 12

2. Выберите правильные варианты ответа. С чем пересекается прямая m?

Решение: при выполнении задания, нужно помнить, что прямая бесконечно продолжается в обе стороны, а отрезок ограничен точками, поэтому, если продолжить прямую m и n, то становится понятно, что они пересекутся между собой. Кроме того, прямая m пересечётся и с отрезком АВ. Следовательно, получается 2 ответа: прямая m пересекается с прямой n и отрезком АВ.

Ответ: прямая m пересекается с прямой n; прямая m пересекается с отрезком АВ.

Источник

Что такое отрезок

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.

Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.

Отрезок — это геометрическая фигура

Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.

На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.

В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.

Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.

Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.

Разница между отрезком, лучом и прямой

Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:

Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.

Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.

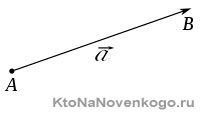
Направленный отрезок — это вектор

Отрезки бывают двух видов:

Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.

Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ ➜ и ВА ➜ — разные отрезки, так как они противоположно направленные.

Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.

Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.

Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.

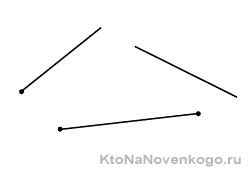
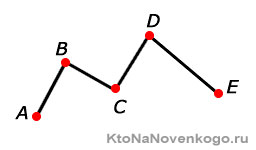
Ломаная линия — это множество соединенных отрезков

Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.

Вершинами ломаной являются следующие точки:

Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.

Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.

Любая замкнутая ломаная является геометрической фигурой — многоугольником.

Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.

Отрезок времени

Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.

Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.

Время в целом в таком случае определяется как временная прямая.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Чтобы не путать с лучом, надо просто запомнить, что отрезок — это две точки. То есть эта прямая и на ней две точки — это и называется отрезком.

Это самая простая часть геометрии и надо просто внимательно читать.

Жизнь тоже можно разделить на отрезки и все они будут неотделимо связаны с временем и конкретным человеком.

Источник

Точка и прямая в начертательной геометрии с примерами

Содержание:

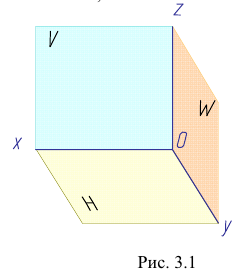
Для полного выявления наружных и внутренних форм деталей и их соединений вводят три и более плоскости проекций.

Введем в систему плоскостей

Чертеж точки

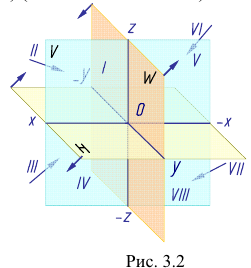
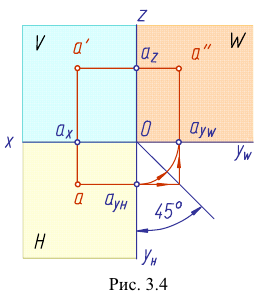
Данное наглядное изображение тонки в системе плоскостей Н, V и W (рис. 3.3) неудобно для черчения из-за сложности. Преобразуем его так, чтобы горизонтальная и профильная плоскости проекций совпали с фронтальной плоскостью проекций, образуя одну плоскость чертежа (рис. 3.4).

Это преобразование осуществляют путем поворота вокруг оси х плоскости Н на угол 90° вниз и плоскости W на угол 90° вправо вокруг оси z. В результате указанного совмещения плоскостей получаем чертеж, называемый эпюр Монжа (от франц, — чертеж, проект).

На эпюре мы не можем показать пространственную картину рас­положения плоскостей проекций и точки. Но эпюр обеспечивает точность изображений при значительной простоте построений.

Таким образом, на комплексном чертеже трех ортогональных проекций точки

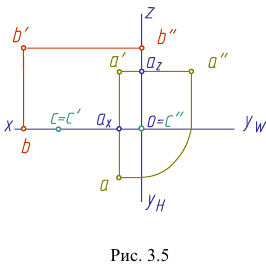
Положение точки в пространстве задается при помощи трех се координат (абсциссы ординаты и аппликаты то есть трех чисел, вы­ражающих расстояние от этой точки до координатных плоскостей проекций. Запись координат точки производят в такой форме: А (х, у, z). Положение точки на плоскости определяют две координаты: а(х,у); a'(x,z); a»(y,z).

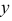
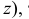
По отношению к плоскостям проекций точка может занимать как общее (точка А), так и частные (точки В и С) положения (рис. 3.5). Если точка лежит в плоскости проекций, то две ее проекции лежат на осях проекций (точка В). У такой точки одна ее координата равна нулю. Если точка принадлежит одновременно двум плоскостям проекций (точка С), то она ле­жит на оси проекций. Две ее проекции совпадают, а третья совпадает с точкой О — началом координат. В атом случае две ее координаты равны нулю. Если точка принадлежит трем плоскостям проекций, то она расположена в начале координат.

Взаимное положение двух точек. Условия видимости на чер­теже

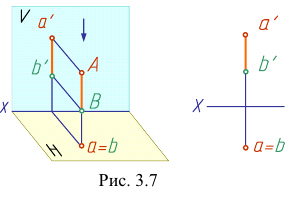
Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?

Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.

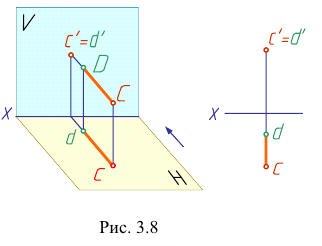
Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).

Из двух профильно-конкурирующих точек на профильной плоскости проекций бу­дет видима та точка, которая расположена левее.

Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).

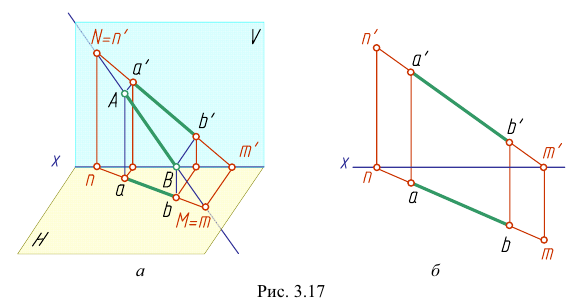
Чертёж отрезка прямой. Прямые частного положения

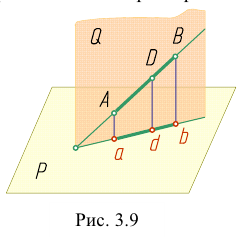
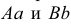
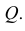
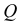
Наглядное изображение отрезка АВ прямой и его ортогональное проецирование на плоскость Р показано на рис. 3.9. Рассмотрим ортогональное проецирование отрезка АВ с учетом свойств параллельного проецирования. Проецирующие прямые образуют проецирующую плоскость Линия пере­сечения плоскостей и Р проходит через проекции а и b точек А и В на плоскости ­ проекций Р. Эта линия и является единственной проекцией прямой АВ на плоскости проекций Р.

Относительно плоскостей проекции прямая может занимать различные положения:

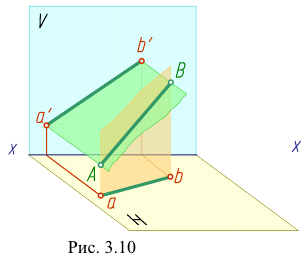
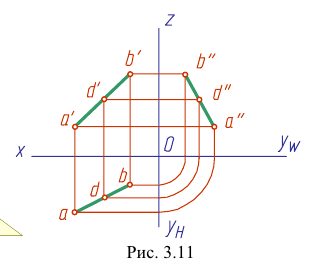
Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения (рис. 3.9 — 3.11).

Прямую, параллельную одной из плоскостей проекций или двум плоскостям проекций (то есть перпендикулярную третьей), называют прямой частного положения.

Различают три вида таких прямых.

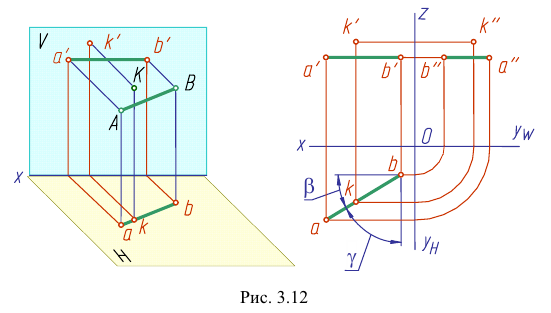
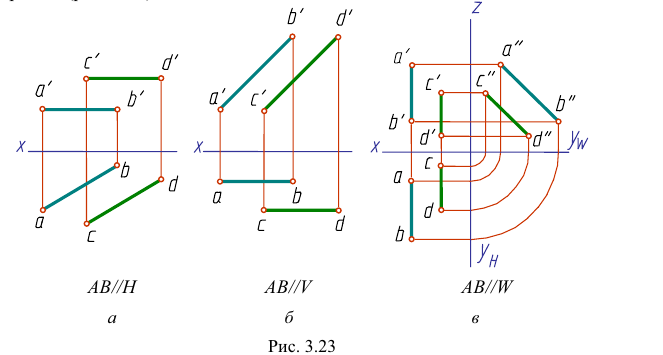
Прямая АВ параллельна плоскости Н

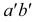
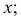
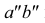
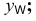
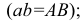
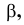
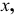
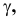
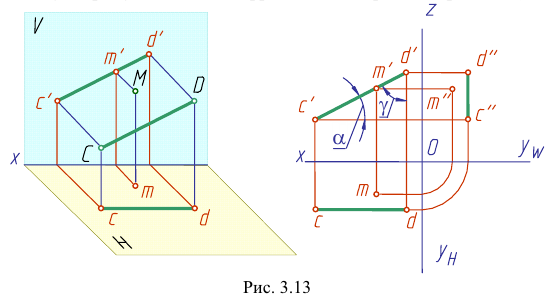
Такую прямую называют «горизонтальной прямой» (рис. 3.12). Фронтальная проекция прямой параллельна оси профильная проекция параллельна оси длина горизонтальной проекции отрезка равна длине самого отрезка угол образованный горизонтальной проекцией и осью проекции равен углу наклона прямой к фронтальной плоскости проекций; угол образованный горизонтальной проекцией и осью проекции равен углу наклона прямой к профильной плоскости проекций:

Прямая CD параллельна плоскости V

Такую прямую называют «фронтальной прямой» (рис. 3.13).

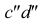
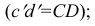
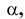
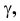
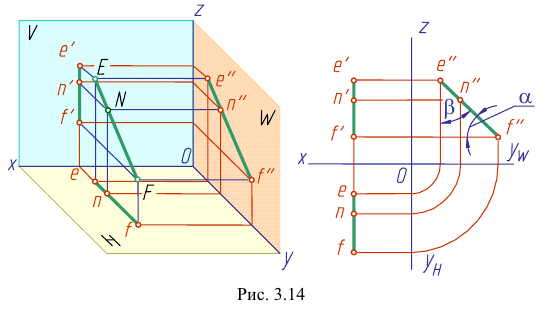
Горизонтальная проекция прямой cd параллельна оси х; профиль­ная проекция параллельна оси z; длина фронтальной проекции отрезка равна длине самого отрезка угол образованный фронтальной проекцией и осью проекций х, равен углу наклона прямой к горизонтальной плоскости проекций; угол образованный фронталь­ной проекцией и осью z, равен углу наклона прямой к профильной плоскости проекций:

Прямая EF параллельна плоскости IF

Такая прямая носит название «профильная прямая» (рис. 3.14).

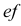
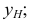
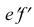
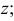
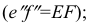
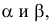
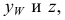
Горизонтальная проекция прямой параллельна оси фронтальная проекция параллельна оси длина профильной проекции отрезка равна длине самого отрезка углы образованные профильной проекцией с осями равны углам наклона прямой к горизонтальной и фронтальной плоскостям проекций соответственно:

Следовательно, каждая линия уровня проецируется в истинную величину на ту плоскость проекции, которой она параллельна. На ту­ же плоскость проекций проецируются без искажения и углы, которые эта прямая образует с остальными двумя плоскостями проекций.

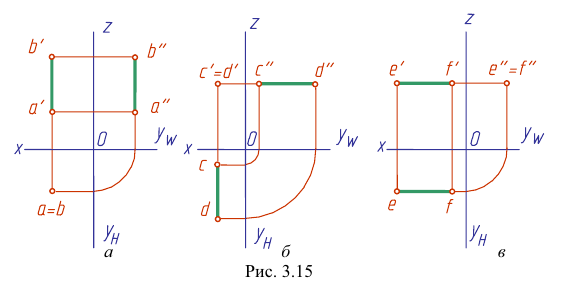
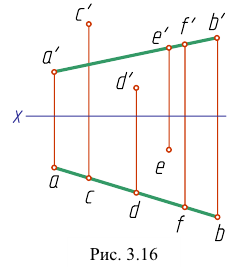
На рис. 3.15 приведены чертежи прямых, перпендикулярных плоскостям проекций. Такие прямые называются проецирующими прямыми. Различают три вида таких прямых.

Прямая АВ перпендикулярна плоскости Н

Прямая CD перпендикулярна плоскости V

Прямая EF перпендикулярна плоскости W

Из чертежа видно, что проецирующая прямая является вместе с тем и прямой двойного уровня, так как она параллельна одновременно двум другим плоскостям проекций

Взаимное положение точки и прямой

Точка и прямая в пространстве могут быть различно расположены относительно друг друга и плоскости проекций.

Если точка в пространстве принадлежит прямой, то ее проекции принадлежат соответствующим проекциям этой прямой.

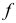
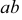
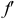
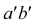
Рассмотрим еще раз это положение на плоскостном чертеже (рис. 3.16). Точка F принадлежит прямой АВ, так как горизонтальная проекция точки принадлежит горизонтальной проекции прямой, а фронтальная проекция точки принадлежит фронтальной проекции пря­мой:

Точка С лежит над прямой АВ, точка D лежит под прямой АВ. точка Е лежит за прямой АВ.

Следы прямой

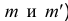
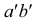
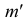
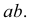
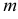
Чтобы построить на плоскостном чертеже горизонтальный след прямой (точки , надо продолжить фронтальную проекцию прямой до пересечения с осью х (точка ). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением горизонтальной проекции Точка — горизонтальная проекция горизонтального следа.

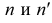
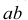
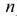
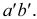
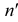
Для построения проекций фронтального следа (точек ) необ­ходимо продолжить горизонтальную проекцию прямой до пересечения с осью х (точка ). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением фронтальной проекции Точка — фронтальная проекция фронтального следа. Построение проекций следов прямой показано на рис. 3.17, б.

Прямая может пересекать и профильную плоскость проекций, то есть иметь профильный след. Этот след на профильной плоскости проекций совпадает со своей проекцией. Фронтальная и горизонтальная проекции его лежат соответственно на осях

Взаимное положение двух прямых

Прямые в пространстве могут занимать различные взаимные поло­жения:

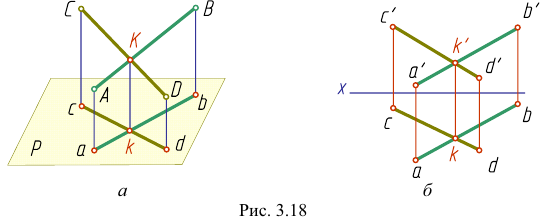
Пересекающиеся прямые

Если прямые пересекаются, то их одноименные проекции пересекаются между собой и точки пересечения проекций лежат на одной линии связи.

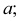
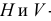
Наглядное изображение двух прямых АВ и CD, пересекающихся в точке К, приведено на рис. 3.18, их чертеж в системе плоскостей -на рис. 3.18, б.

Если одна из прямых профильная, то чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.

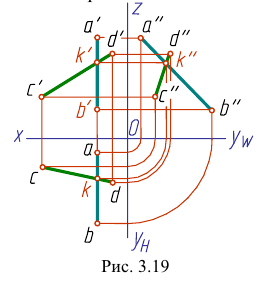
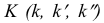
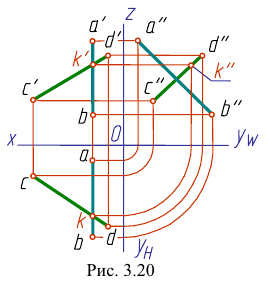
На рис. 3.19 все проекции точки одновременно принадлежат проекциям прямой АВ и прямой CD. Это значит, что прямые АВ и CD пересекаются.

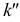
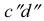
На рис. 3.20 профильная проекция точки К принадлежит профильной проекции и не принадлежит профильной проекции

Это значит, что прямые АВ и CD не пересекаются, они скрещиваются.

Параллельные прямые

О параллельности прямых в пространстве можно судить по параллельности их одноименных проекций на двух плоскостях проекций.

При этом нужно учитывать некоторые условия.

Для прямых общего положения:

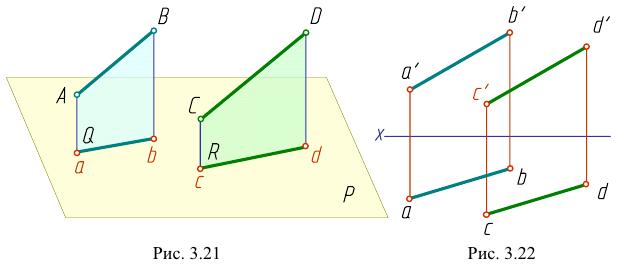
Если одноименные проекции прямых общего положения парал­лельны в системе двух любых плоскостей проекций, то прямые парал­ лельны (рис. 3.22).

Для прямых частного положения:

Если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые (рис. 3.23).

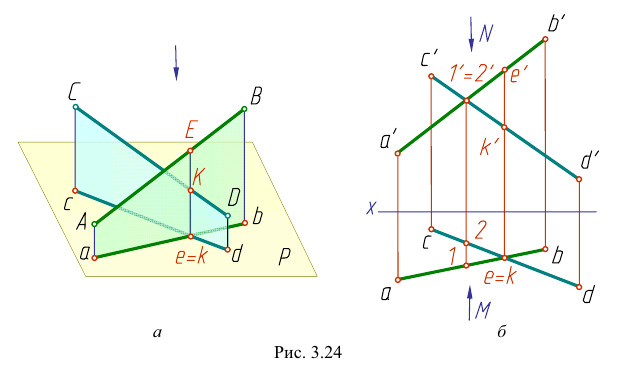
Скрещивающиеся прямые

Если прямые в пространстве нс пересекаются, а скрещиваются (рис. 3.24), то хотя на чертеже их одноименные проекции и пересекаются, но точки пересечения проекций не лежат на одной линии связи. Эти точки не являются общими для прямых.

Сравнивая положение таких точек, определяют, какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю. На рис. 3.24, а видно, что точка Е (принадлежащая прямой АВ) расположена выше точки К (принадлежащей прямой CD). При взгляде сверху по указанной стрелке точка Е закрывает точку К. Соответственно и на чертеже (рис. 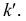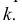3.24, б) фронтальная проекция е’ расположена выше фронтальной проекции При взгляде сверху по стрелке N при проецировании на плоскость Н точка е закрывает точку Прямая АВ проходит над прямой CD.

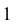
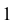
На плоскости V совпадают фронтальные проекции 1′ и 2′ точек прямых АВ и CD. При взгляде спереди по стрелке М видно, что точка прямой АВ находится ближе к наблюдателю, и при проецировании на плоскость V точка прямой АВ закрывает точку 2 прямой CD. Прямая АВ расположена ближе к наблюдателю. Рассмотренные точки являются конкурирующими, так как они лежат на одной линии связи, но на разных прямых.

Проецирование плоских углов

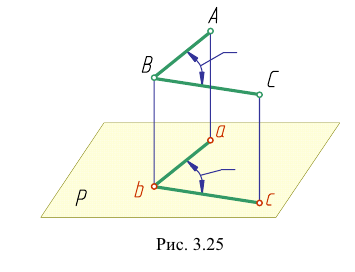
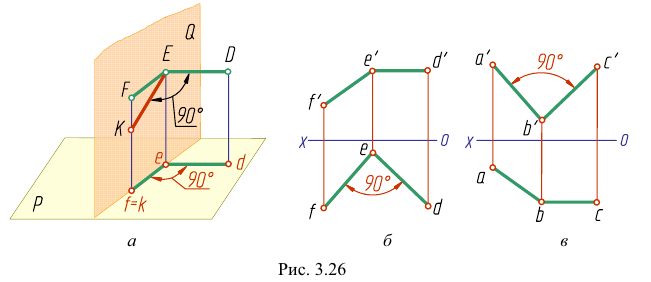
Любой линейный угол образуется двумя пересекающимися пря­мыми. На плоскости проекций он проецируется в общем случае с искажением. Однако, если обе стороны угла параллельны какой-либо плоскости проекций, то на эту плоскость угол проецируется без искажения. Например, стороны угла АВС (рис. 3.25) параллельны горизонтальной плоскости Р. поэтому угол 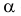спроецировался на нее без изменений.

Исключение составляет прямой угол. Он проецируется в истинную величину даже тогда, когда лишь одна из его сторон параллельна плоскости проекций. Рассмотрим теорему о проецировании прямого уг­ла.

Доказательство. Пусть угол 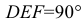и расположен так, что обе его стороны параллельны плоскости Р(рис. 3.26, а). Тогда, как и всякая фигура, лежащая в плоскости, параллельной Р, данный угол спроецируется на Р без искажения, то есть его проекция

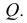
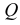
Через прямые EF и Ее проведем дополнительную плоскость Плоскость перпендикулярна плоскости Р.

Но, как видно непосредственно из чертежа, только одна сторона DE угла DEK параллельна плоскости Р.

Вторая сторона его ЕК наклонна к плоскости Р.

Итак, для того чтобы прямой угол проецировался в натуральную величину, достаточно, чтобы одна его сторона была параллельна плоскости проекций (рис. 3.26, б, в).

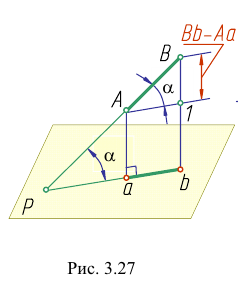
Определение истинной величины отрезка прямой

Отрезки прямых общего положения не проецируются в истинную величину ни на одну из плоскостей проекций. Однако в ряде задач необходимо определить по чертежу длину отрезка прямой общего положения и углы наклона прямой к плоскостям проекций.

В этом случае используют способ построения прямоугольного треугольника.

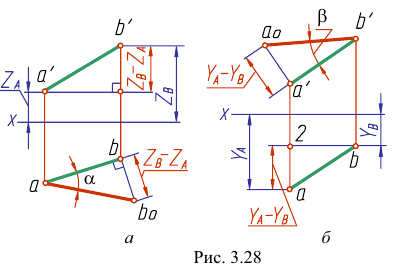
Определим истинную величину отрезка АВ и угол наклона его к плоскости Н (угол 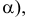если известны две проекции отрезка (рис. 3.28, а).

На рис. 3.28, 6 показано определение истинной величины отрезка АВ и угла наклона его к плоскости V- угла

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник