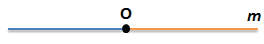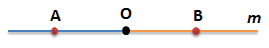Что значит пересекается луч
Что такое луч в математике
Не секрет, что знания, которые вы получили в школьные годы не всегда остаются с вами впоследствии Иногда бывает полезно изучить новое или освежить в памяти то, что вы давно забыли. Сегодня вы вспомните такое понятие как луч.
Луч — геометрическое понятие
Луч — это такая прямая линия, один из концов которой ограничен точкой, а другой продолжается до бесконечности. Таким образом, фигура тянется вперёд без ограничений. но только с одной стороны. Вторая сторона не может тянуться дальше точки, которая является началом фигуры.
На картинке вы можете посмотреть, что такое луч и как он выглядит:
Луч отмечается посредством строчной латинской буквы или двух таких точек, которые обозначены заглавными буквами латинского алфавита.
Если вы увидите отрезок с двумя точками и продолжите его в одну из сторон, как показано на рисунке, то получится луч.
Отличия луча от прямой и от отрезка
В геометрии есть три схожих понятия, которые подразумевают под собой черту — это луч, отрезок, прямая. Эти фигуры всегда изображаются без изгибов и имеют ряд особенностей.
В рамках курса математики луч — это полупрямая. Дело в том, что с одного конца он обладает признаком бесконечности, который присущ прямой линии.
В начальной точке луч имеет сходство с отрезком, так как он так же ограничен точкой.
Обратите внимание — быстро отличить фигуры друг от друга вы можете по наличию у них начала и конца:
Взаимное расположение лучей
Если на прямой линии вы поставите точку, то на ней сформируются два таких луча, начало которых находится в одной точке.
На рисунке начало для лучей — общая точка A.
По взаимному расположению лучи делятся на пересекающиеся и непересекающиеся.
Параллельный луч — это фигура, у которой любая точка находится на одинаковом расстоянии от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.
Дополнительные лучи — это фигуры, которые обладают такими признаками, как:
Можно ли сравнить два луча?
Луч — это такая фигура, которую нельзя измерить. Он продолжается без ограничений, поэтому не обладает характеристикой длины.
Так как невозможно измерить несколько лучей, сравнить их вы тоже не сможете.
Луч — альтернативные значения слова
Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.
Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.
Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:
В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.
Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.
Пересечение луча и прямой на плоскости
Пересечение луча и прямой
Пересечения луча и прямой на плоскости могут иметь общие и частные варианты: луч и прямая пересекаются, луч и прямая параллельны и не пересекаются, луч и прямая параллельны и совпадают, луч и прямая расположены под углом друг к другу и не пересекаются. Выведем уравнения и вычисления теоретически и затем воплотим их в практический программный код на C#.
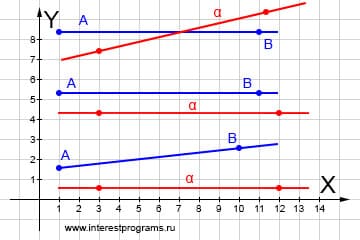
Определение наличия пересечения
В тетраде мы можем видеть явное пересечение когда луч пересекает прямую. Но можно нарисовать луч и прямую так что они почти параллельны, тогда как узнать пересекаются или нет? В программном коде все случаи необходимо скрупулезно разбирать, вслепую полагаясь только на вычисления. Определить наличие пересечения можно решив систему из уравнений луча и прямой.
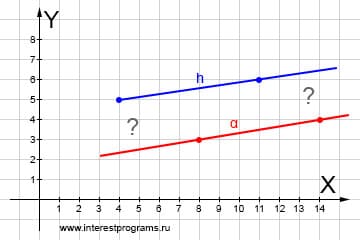
Возьмем параметрические уравнения для луча и с коэффициентами для прямой. Параметрическое уравнение луча отличается важным параметром t идентифицирующий направление луча. Только при t >=0 уравнение определяет множество точек луча. Если же к лучу добавить точки при t = 0 луч и прямая пересекаются, если t
Точка пересечения луча и прямой
Теперь определим на примере точку пересечения луча и прямой. Сформируем необходимые данные для системы уравнений (у.1) и сначала определим факт пересечения уравнение (у.2), затем получим координаты точки С.
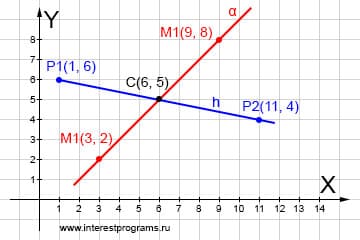
Используем выражение (у.2) для параметра t и подставив данные получим значение: Искомые координаты:
Луч и прямая не пересекаются
Необходимо заметить, что если даже t
Уравнение в программный код
Из теоретических утверждений создадим практический программный код, вычисляющий точку пересечения луча и прямой. Необходимо также в коде создать защиту от возможных исключений. Код будем строить, опять же, используя систему уравнений (у.1) выведенную выше.
Начинаем с определения переменных для входных и выходных данных. Рекомендуется использовать тип Double для повышенной точности расчетов. Кроме вычисления точки пересечения необходимо предусмотреть мягкий обход деления на ноль.
Теперь выражение для получения параметра t. Если t >= 0 точка луч и прямая пересекаются. Если t
Деление на ноль
Как видно из выражения вывода параметра t нам не удалось избавится от деления. В случае если знаменатель будет равен нулю, то результат будет бесконечность. В каких случаях знаменатель может быть равен нулю?
В этих трех случаях, при вычислении параметра t, сработает исключение в результате деления на ноль. В программном коде необходимо предусмотреть обход генерирования исключительной ситуации.
Параллельность луча и прямой
Доказано что если луч и прямая параллельны друг другу, то у них нет общих точек. Чтобы установить параллельность луча и прямой достаточно сравнить их вектора направления. Если направление векторов совпадает, значит они коллинеарны т.е. параллельны или совпадают.
Проверка на параллельность: Если направление векторов совпадает, то должно выполняться условие: Без операции деления:
Совпадение луча и прямой
Частный случай параллельности, когда луч и прямая совпадают. При совпадении они имеют бесконечное количество общих точек. Для программного кода программ и игр это значит, как такового пересечения нет, нет конкретных координат пересечения.
Если две точки луча лежат на прямой, значит луч и прямая совпадают. Подставим координаты луча в уравнение прямой. Если уравнение верно, то две контрольные точки луча лежат на прямой. Значит луч и прямая совпадают.
Координаты луча являются решениями для уравнения прямой, значит две точки луча принадлежат прямой. Отсюда вывод: луч и прямая совпадают.
Программный код
Демонстрационная программа
Луч в математике — определение, форма и свойства
Геометрия занимается изучением разных фигур и их свойств. К ним относятся квадрат, треугольник, круг, овал, цилиндр. Луч в математике — это такая прямая, у которой нет конца. Поэтому она считается бесконечной. С данным понятием впервые сталкиваются ученики начальной школы. Более подробно материал изучается в 5 классе. Для решения задач по заданной тематике изучаются плоскость, отрезок, биссектриса.
Трактовка понятий
Впервые термин «луч» использовал в 1833 году швейцарский учёный Якоб Штейнер. Для его определения потребуется на плоскости поставить точку. Из неё должна исходить часть прямой, которая состоит из множества точек, расположенных по одну сторону от первоначальной. Само понятие «точка» считается абстрактным объектом, который не имеет высоты, радиуса, длины, сторон, угла. В задачах важно её местоположение на плоскости либо полуплоскости.
На чертеже она обозначается заглавной латинской буквой. Чтобы различить несколько точек, на рисунке используется несколько букв. Можно вводить числовое обозначение. В отличие от луча, отрезок считается частью прямой, ограниченной двумя точками на концах. Множество точек образует линию, у которой нет толщины и ширины. На плоскости можно начертить следующие её виды:
Линии пересекаются, если имеют одну общую точку. Чтобы они были перпендикулярны друг другу, между ними должен образовываться угол в 90 градусов. При параллельности части прямой не могут скрещиваться.
К особым формам луча относится ломаная. Она состоит из последовательно соединенных отрезков (звенья) под углом, отличным от 180°. Смежные звенья находятся на разных прямых.
У ломаной есть вершины. Они могут обозначаться с помощью латинских заглавных букв. Их нельзя править на маленькие. Сама вершина считается точкой, откуда начинается одна ломаная и заканчивается другая. Основным примером замкнутой линии является многоугольник. Его стороны представлены в виде звеньев.
Описание лучей
В геометрических задачах встречаются дополнительные лучи. Чтобы их начертить, потребуется отобразить на плоскости прямую, разделённую точкой на две полупрямые. Каждая часть является дополнительной относительно другой. Свойства лучей:
Дополнительные лучи могут дополнять друг друга до прямой. Отдельно рассматриваются совпадающие лучи. Если их наложить друг на друга, они совпадут. Для них характерна равная длина.
Чтобы отметить лучи на рисунке, используются порядковые номера.
Незамкнутый открытый луч состоит из точек, находящихся по одну сторону относительно проведённой линии. Для его обозначения используется строчная латинская буква либо две заглавные. Одна точка является началом, а вторая размещается на самом луче. В основе такой фигуры находятся полупрямые. Если в условиях задачи дана линия, формула выглядит следующим образом: (АB). Отрезок записывается в квадратных скобках.
Принципы классификации
Так как луч является частью прямой, поэтому через любую его точку проводится множество прямых, но только через две несовпадающие проходит одна прямая. Луч можно изобразить в нескольких вариантах: пересечение, скрещивание и параллельность.
Чтобы задать луч на плоскости, используется линейное уравнение. Фигуры называются разными способами и с помощью знаков. Можно провести полупрямую «О». Её начальная точка считается исходной и другой не существует. Другой способ записи — использование нескольких букв в середине либо в иных частях линии. Если в задаче дана прямая, её можно обозначить двумя буквами, размещёнными в разных её частях, к примеру, (АB).
Третий метод обозначения: точка «О» находится с некоторым отступом от начала. Центральную часть можно назвать буквой К. В таком случае весь луч будет называться ОК. Если нужно начертить продолжение к прямой, понадобится отметить на чертеже линию и точку, которая будет считаться производной. С помощью последней фигуры делится первая на 2 линии, которые не пересекаются между собой. Чтобы обозначить продолжение, рисуется линия карандашом.
Она будет иметь общее начало с основополагающей, но не будет совпадать с ней. Из т. О проводится прямая, не располагающаяся на дополняющих, но имеющая с ними одно общее начало. На новом луче отмечается т. В. На продолжении лежит отрезок ОВ.
Неразвернутый угол является случаем луча. Если стороны первой фигуры представлены в виде дополнительных полупрямых одной прямой, тогда угол является развёрнутым. Его значение равняется 180 градусов. Если значение угла иное, тогда он неразвернутый.
Следует отличать геометрические лучи от световых.
В математике фигура представлена в виде линии, у которой нет ничего общего с энергией. Для световых лучей характерно несконцентрированное направление, дефракция (переломанный). Но при сильном потоке света наблюдается их чёткое направление.
Аксиомы и доказательства
Свойства лучей определяются аксиомами. Положение 1: на любом луче от начала можно отложить отрезок определённой длины, и только один.
Доказательство: если на линии от начала А отложить 2 равных отрезка АВ и АС, тогда точки С и В совпадут. В и А не лежат на прямой, а находятся с одной стороны от неё. Если отрезок АВ не пересекает эту прямую, тогда множество точек, лежащих с единой стороны от прямой, называется полуплоскостью. При доказательстве положения 1 следует ориентироваться на определение луча.
Аксиома: прямая разделяет плоскость на 2 полуплоскости. Следствие: если D и С находятся в различных полуплоскостях от прямой а, тогда отрезок DC пересекает а. Из этого вытекает теорема: A, B, O, C расположены на прямой а таким образом, что А и В находятся с одной стороны от т. О, т. С и В — с одной стороны от О. При этом А и С размещены с одной стороны от О.
Доказательство: нужно провести через О прямую b, которая отлична от а. Она будет разбивать плоскость на 2 полуплоскости. На одной из них находится т. В. Так как отрезки BC и AB не пересекают прямую b, поэтому точки А и С находятся в одной полуплоскости с В. Отрезок АС не пересекает b. На нём не находится т. О. От неё по одну сторону размещены т. А и С.
Предположение: если O, A, B, C принадлежат прямой а, при этом А находится между В и О, тогда А лежит между О и С. По одну сторону от О находятся три точки А, B и C.
Доказательство: так как по условию т. А находится между О и В, поэтому А и В лежат по одну сторону от О. По второму условию В и С лежат по эту же сторону от О. Исходя из теоремы 1, А, В и С лежат по одну сторону от т. О.
Теорема: если O, A, B, C принадлежат одной линии а, т. А лежит между В и О, а т. В между О и С, тогда В находится между А и С.
Доказательство: выдвигается предположение, что из условия теоремы заключение не следует. Точка В не находится между А и С. По свойству взаиморасположения A, B, C, точки А и С лежат по одну сторону от В. По предположению следует, что они лежат по одну сторону от О, либо A, C, O лежат по одну сторону от B. Это противоречит условию: О и С находятся по разные стороны от В, либо А и С размещены по иную сторону от В, в отличие от т. О.
Подобное противоречит условию принадлежности А отрезку ОВ. Такое противоречие показывает, что предположение о т. В, не лежащей между А и С, неверное. Следовательно, точка В находится между А и С, что доказывает теорему. При решении геометрических задач, связанных с плоскостью и фигурами на ней, учитываются основные теоремы, доказанные учеными за всю историю математики.
Плоскость, прямая линия, луч
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Обозначение прямой
Например, на рисунке 1 обозначены такие прямые:
Рис. 1 Обозначение прямой линии
Рис. 2 Обозначение прямой с несколькими точками
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
Рис. 5 Пересечение прямых
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
Луч имеет второе название – полупрямая.
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 22
Что значит пересекается луч
Построим прямую АВ
(прямая обозначена двумя большими латинскими буквами, например, А и В)
Отметим на прямой АВ точку О
Точка О разбивает прямую АВ на две части (влево от точки О и вправо от точки О)
Части, на которые точка О разбивает прямую АВ, выделены цветом
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча
Назовем получившиеся лучи:
Луч является геометрической фигурой
Луч — это часть прямой, ограниченная с одной стороны
Луч имеет начало, но не имеет конца
Другой способ обозначений
Построим прямую m
(прямая обозначена малой латинской буквой, например, m)
Точка О разбивает прямую m на два луча
Назовем получившиеся лучи
Варианты обозначения лучей
Луч ОВ (обозначение двумя большими латинскими буквами)
Луч ОВ (обозначение двумя большими латинскими буквами)
Луч k (обозначение малой латинской буквой)
Начало луча обозначено буквой О
Луч k (обозначение малой латинской буквой)
Начало луча не обозначено буквой (только отмечено точкой)
Дополнительные лучи
Лучи ОА и ОВ принадлежат одной прямой АВ
Лучи ОА и ОВ имеют общее начало (точка О)
Лучи ОА и ОВ противоположно направлены
При таких условиях лучи ОА и ОВ называются дополнительными
Поделись с друзьями в социальных сетях: