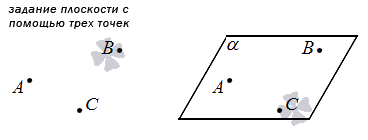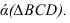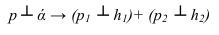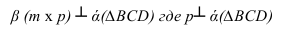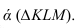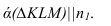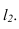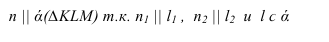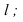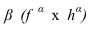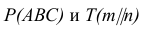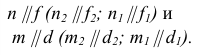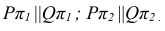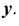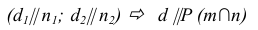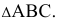Что значит пересекает плоскость

Плоскость в пространстве – необходимые сведения

Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.

Понятие плоскости и ее обозначения

Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.

В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.

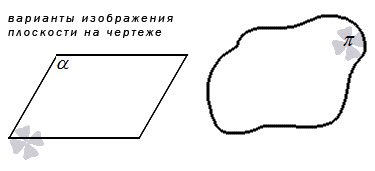
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.

Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.

Как могут располагаться плоскость и точка друг относительно друга

Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:

В любой плоскости есть точки.

Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.

Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.

Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:

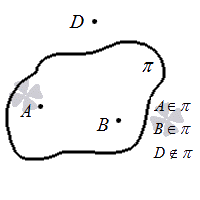
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.

Графически последнюю аксиому можно представить так:

Варианты взаимного расположения прямой и плоскости

Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:

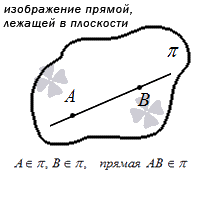
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.

Графически этот вариант расположения выглядит так:

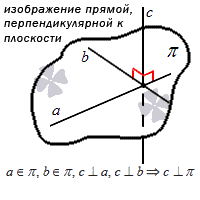
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.

Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.

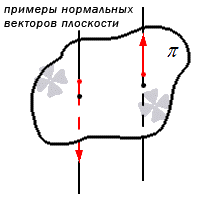
Примеры нормальных векторов плоскости показаны на рисунке:

Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.

Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.

Варианты расположения двух плоскостей друг относительно друга

1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.

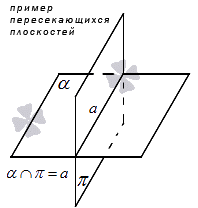
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:

Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.

На графике это будет выглядеть так:

В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.

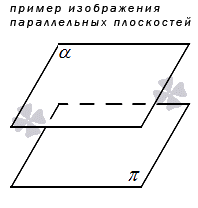
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.

Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.

Как задать плоскость в пространстве

В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.

1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.

Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:

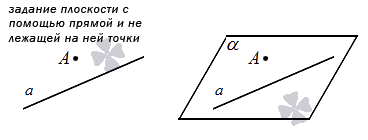
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:

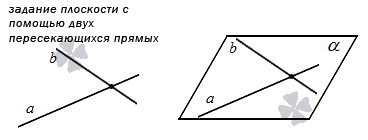
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:

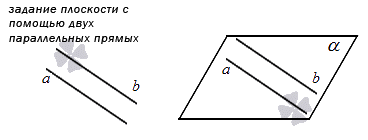
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.

На рисунке этот способ будет выглядеть так:

Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:

Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.

Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).

Вспомним одну теорему, изученную в рамках курса по геометрии:

Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.

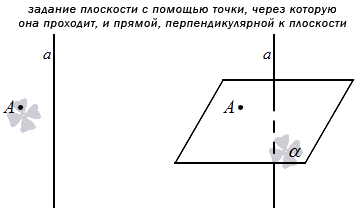
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.

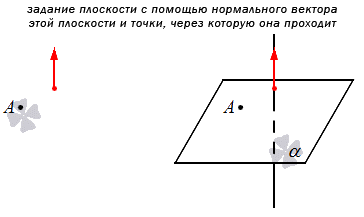
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.

Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.

Источник

Взаимное положение прямой и плоскости с примерами

Содержание:

Проекции прямого угла:

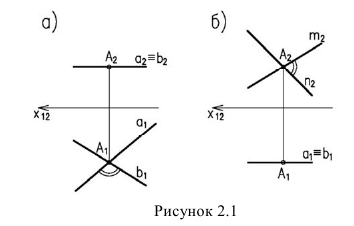
Величина угла между двумя пересекающимися прямыми в общем случае на проекциях искажается. В натуральную величину этот угол будет проецироваться в том случае, если плоскость угла параллельна одной из плоскостей проекций. Тогда другие проекции сторон угла совпадают и параллельны оси проекций (рисунок 2.1).

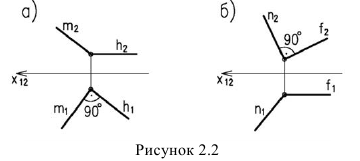
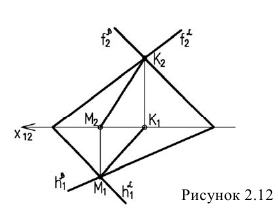
Прямой угол проецируется в натуральную величину, если одна из его сторон параллельна одной из плоскостей проекций (рисунок 2.2).

Взаимное положение примой и плоскости, двух плоскостей

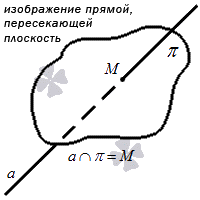
Прямая относительно плоскости может занимать следующие положения: лежать в плоскости (что рассматривалось ранее); быть ей параллельна; пересекать плоскость; быть перпендикулярной плоскости (т.е. пересекать под прямым углом).

Две плоскости могут быть:

Перпендикулярность примой и плоскости

Условие перпендикулярности прямой и плоскости:

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости.

Так как прямой угол между прямыми линиями проецируется на плоскость проекций без искажения, если одна из прямых параллельна этой плоскости проекций, то пересекающимися прямыми плоскости, которые нужно взять для построения перпендикуляра, могут быть только ее горизонталь и фронталь.

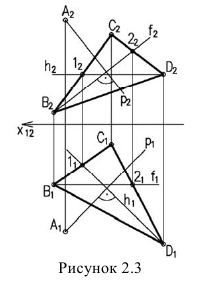
Следовательно, прямая перпендикулярна плоскости, если ее фронтальная проекция перпендикулярна фронтальной проекции фронгали плоскости, а горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости.

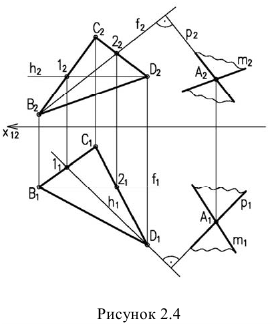
На рисунке 2.3 через точку 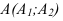проведена прямая, перпендикулярная плоскости

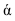
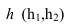
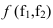
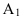
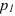
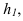
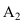
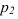
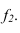
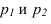
В плоскости проведены горизонталь и фронталь, затем через проведена горизонтальная проекция перпендикуляра под прямым углом к а через точку фронтальная проекция перпендикуляра иод прямым углом к Прямые есть проекции искомого перпендикуляра р.

Перпендикулярности двух плоскостей

Две плоскости взаимно перпендикулярны, если одна из них содержи! перпендикуляр к другой.

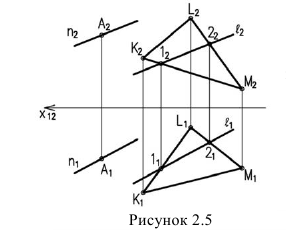
Пусть через данную прямую т необходимо провести плоскость, перпендикулярную плоскости а. заданной треугольником 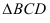(рисунок 2.4).

Для решения задачи достаточно на прямой т взять произвольную точку А и провести через нее прямую р, перпендикулярную данной плоскости .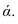

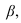
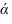
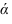
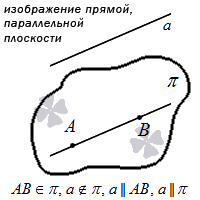
Пересекающиеся прямые m и р образуют плоскость которая содержит прямую р, перпендикулярную плоскости следовательно, плоскости (i и взаимно перпендикулярны.

Параллельность прямой и плоскости

Условие параллельности прямой и плоскости:

Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости.

Рассмотрим пример решения задачи на параллельности прямой и плоскости.

Задача: построить фронтальную проекцию прямой n, проходящей через точку А и параллельной

Для решения задачи:

Проводим горизонтальную проекцию прямой 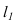в плоскости

Строим фронтальную проекцию

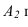
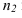
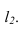
Через точку проводим параллельную Таким образом получим:

Параллельность двух плоскостей

Условие параллельности двух плоскостей:

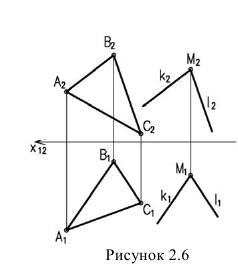
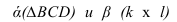
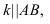
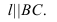
Изображенные на рисунке 2.6 плоскости взаимнопараллельныe, т.к. Пересечение прямой и плоскости

Задача на нахождение точки пересечения прямой линии с плоскостью является первой основной позиционной задачей курса начертательной геометрии.

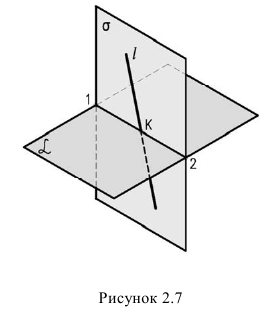
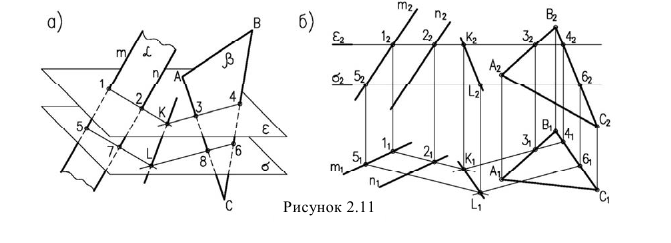
Алгоритм решения задачи (рисунок 2.7):

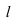
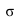
1. Прямую заключаем во вспомогательную плоскость (удобнее всего в проецирующую);

2. Находим линию пересечения (1-2) вспомогательной плоскости с заданной

3. Отмечаем точку пересечения К найденной линии пересечения (1-2) с заданной прямой

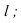
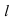
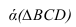
4. Определяем видимость прямой На основании данного алгоритма определим точку пересечения прямой с плоскостью (рисунок 2.8) и с плоскостью

Пересечение двух плоскостей

Две плоскости пересекаются по прямой линии, поэтому для её построения достаточно найти две точки одновременно принадлежащие двум плоскостям.

Рассмотрим несколько случаев построения линии пересечения двух плоскостей.

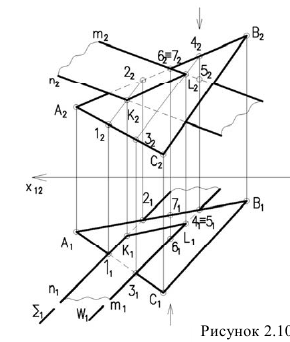
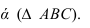
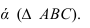
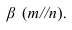
Задача сводится к нахождению точек пересечения прямых m и n с плоскостью а. Соединив точки пересечения К и М получим линию пересечения плоскости с плоскостью Видимость определяется по конкурирующим точкам.

Алгоритм решения задачи (рисунок 2.11):

Видимость при этом не определяется.

В данном случае в качестве плоскостей-посредников могут быть использованы плоскость проекций.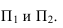

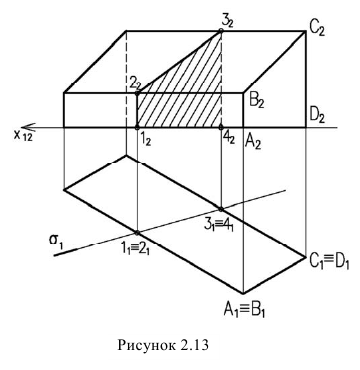
Пересечение многогранника проецирующей плоскостью

Так как секущая плоскость горизонтально-проецирующая, то фронтальную проекцию сечения можно построить, определив точку пересечения каждого ребра с плоскостью о (рисунок 2.13)

Взаимное положение двух плоскостей

Две плоскости могут принадлежать одна другой; быть параллельны или пересекаться.

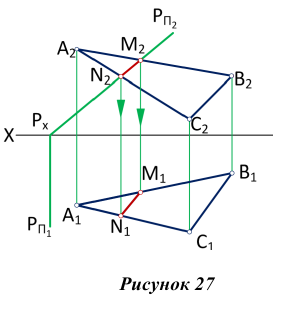
Пересечение плоскости общего положения с плоскостью частного положения

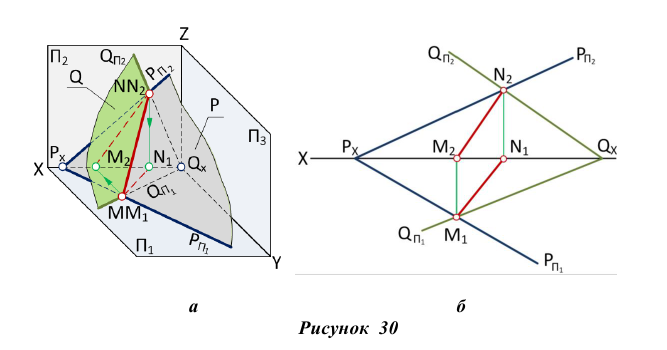
На рис. 27 показано построение линии пересечения фронтально-проецирующей плоскости Р с плоскостью треугольника AВС.
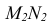
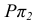
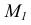
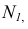
Так как линия пересечения двух плоскостей принадлежит фронтально-проецирующей плоскости Р, то ее фронтальная проекция совпадает с фронтальным следом плоскости Р. Горизонтальная проекция искомой линии пройдет через точки и расположенные на горизонтальных проекциях AВ и АС соответствующих сторон треугольника (рис. 27).

Пересечение двух плоскостей общего положения

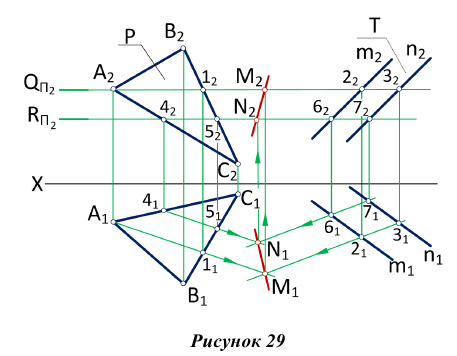
Задача. Построить линию пересечения двух плоскостей общего положения

Алгоритм решения задачи (рис. 28)

Плоскости параллельны

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.

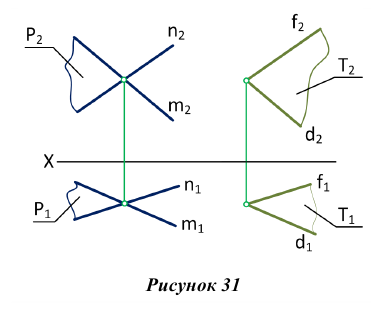
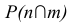
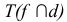
Изображенные на рис. 31 плоскости и параллельны, т.к.

Плоскости общего положения также параллельны, если два любых одноименных следа параллельны между собой.

Изображенные на рис. 32 плоскости Р и Q параллельны, т.к.

Взаимное положение прямой линии и плоскости

Прямая может лежать в плоскости, пересекать плоскость и быть параллельной плоскости.

Пересечение прямой линии с плоскостью частного положения

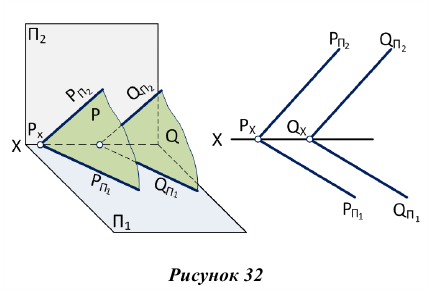
Если заданная плоскость перпендикулярна к какой-либо плоскости проекций (рис.33, а), то она проецируется на эту плоскость проекций в виде прямой линии, на которой обязательно будут находиться соответствующие проекции всех точек, принадлежащих данной плоскости, в том числе и проекции точки пересечения какой-то прямой с заданной плоскостью (точка встречи прямой с плоскостью). Поэтому точка встречи прямой с плоскостью частного положения находится па эпюре без дополнительных построений (рис. 33,6).

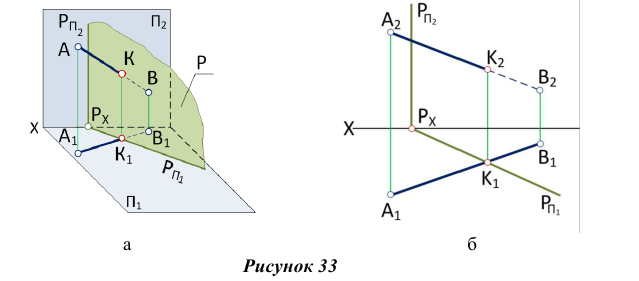
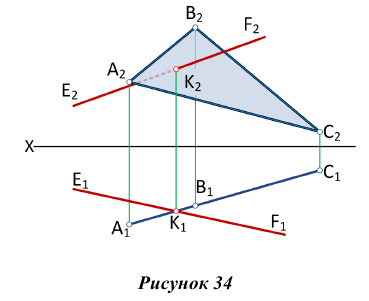
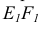
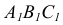
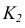
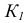
На рис. 34 точка встречи прямой EF с горизонтально-проецирующей плоскостью, заданной треугольником ABC, является точкой пересечения горизонтальных проекций и прямой и треугольника. Фронтальная проекция точки пересечения лежит на линии проекционной связи, проведенной из точки до пересечения с фронтальной проекций прямой EF. Принято считать, что всякая плоскость (в том числе и плоскость проекций) непрозрачна. Поэтому часть прямой, которая находится за плоскостью, является невидимой и показана на эпюрах (рис. 33,6; 34) штриховой линией.

Определение видимости на эпюрах

Вопрос о видимости линий или поверхностей всегда может быть сведен к вопросу о видимости точек. Если несколько точек находятся на общей для них линии связи, то видимой будет только одна из них — наиболее удаленная от той плоскости проекций, по отношению к которой определяется видимость.

Точки, расположенные на одной линии связи, называются конкурирующими. Точки А, В и С, D — конкурирующие (рис. 35).

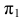
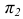
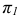
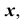
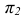
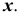
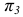
Относительно плоскости проекций видимой будет точка А; относительно плоскости проекций видимой будет точка D, т. е. относительно плоскости видимой будет та точка, фронтальная проекция которой находится дальше от оси а относительно плоскости видимой будет та точка, горизонтальная проекция которой находится дальше от оси Аналогично: относительно плоскости видимой будет та точка, горизонтальная проекция которой будет находиться дальше от оси

Пересечение прямой линии с плоскостью общего положения

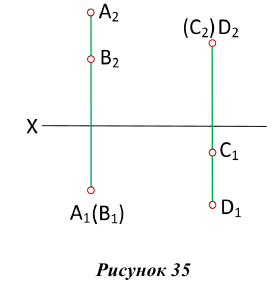
Точку пересечения прямой линии АВ с плоскостью общего положения Р (рис. 36) находят следующим образом:

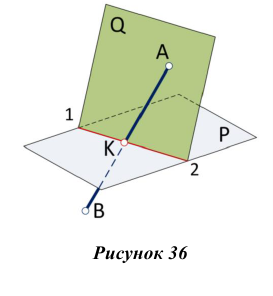
Пошаговые построения по определению точки пересечения прямой АВ с плоскостью треугольника CDE на эпюре приведены на рис. 37 (а-в).

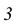
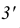
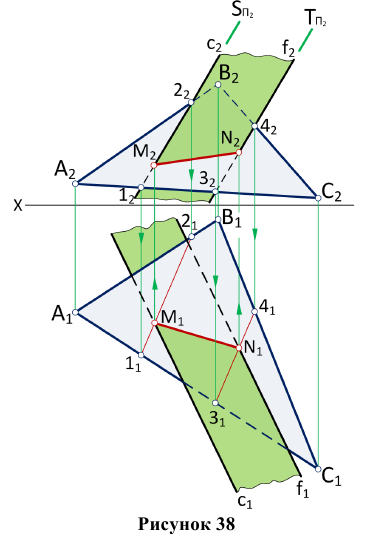
Аналогично, используя конкурирующие точки и определяем видимость прямой АВ и плоскости по отношению к фронтальной плоскости проекций.

Задачи, на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение прямой с плоскостью.

Одна из изображенных на рис. 38 плоскостей задана треугольником AВС, а вторая — двумя параллельными прямыми с и f.

Точка N найдена аналогично. Прямая MN — искомая. Видимость на рис. 86 определена из условия, что заданные плоскости ограничены треугольником и двумя параллельными прямыми, определяющими их.

Прямая параллельна плоскости

На рис. 39 через точку С проведена прямая d, параллельная плоскости Р, заданной пересекающимися прямыми т и п.

Прямая d параллельна прямой n, принадлежащей плоскости 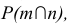следовательно, прямая d параллельна этой плоскости:

Прямая перпендикулярна плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

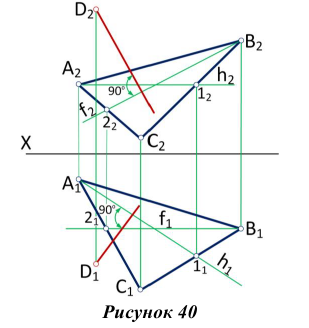
Чтобы построить перпендикуляр из точки D на плоскость треугольника AВС (рис.40) необходимо предварительно построить
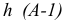
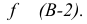
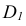
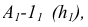
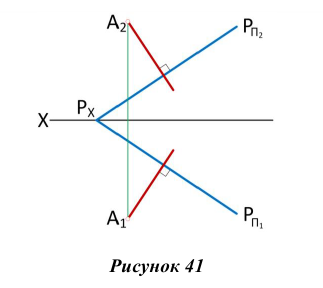
горизонталь и фронталь плоскости Горизонтальная проекция перпендикуляра пройдет через точку перпендикулярно к горизонтальной проекции горизонтали а фронтальная проекция — перпендикулярно к фронтальной проекции фронтали

Если же плоскость задана следами, то, учитывая, что фронтальная проекция любой фронтали в этой плоскости всегда параллельна фронтальному следу плоскости, а горизонтальная проекция любой горизонтали параллельна горизонтальному следу плоскости, легко видеть (рис. 41), что проекции перпендикуляра к плоскости должны быть перпендикулярны соответствующим следам плоскости.

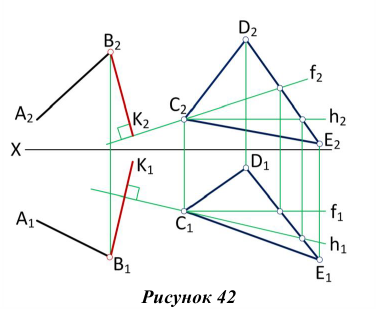
Плоскости перпендикулярны

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. На рис. 42 через прямую АВ проведена плоскость, перпендикулярная плоскости треугольника CDE. Для этого из точки В прямой АВ восстановлен перпендикуляр ВК к плоскости треугольника 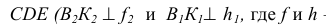— фронталь и горизонталь плоскости треугольника CDЕ ). Плоскость, определяемая пересекающимися прямыми АВ и ВК— искомая.

Если возникает необходимость в построении взаимно перпендикулярных прямых общего положения, необходимо построить плоскость, перпендикулярную заданной прямой, и взять в ней любую прямую.

Задача.

Через точку М провести прямую, перпендикулярную прямой

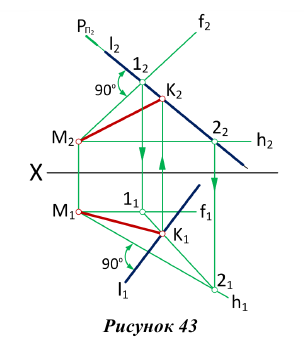
Для построения взаимно перпендикулярных прямых (рис. 43), одна из которых 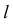задана, а вторая (чтобы задача имела единственное решение) должна проходить через какую-либо определенную точку М, надо выполнить следующее:

Задача:

Определить расстояние от точки до плоскости, заданной треугольником ABC (рис.44)

Расстояние от точки до плоскости определяется длиной перпендикуляра, опущенного из точки на плоскость. Поэтому решение этой задачи выполняем в следующей последовательности:

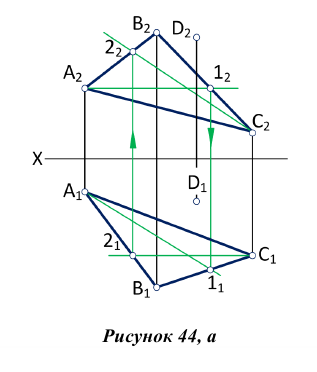
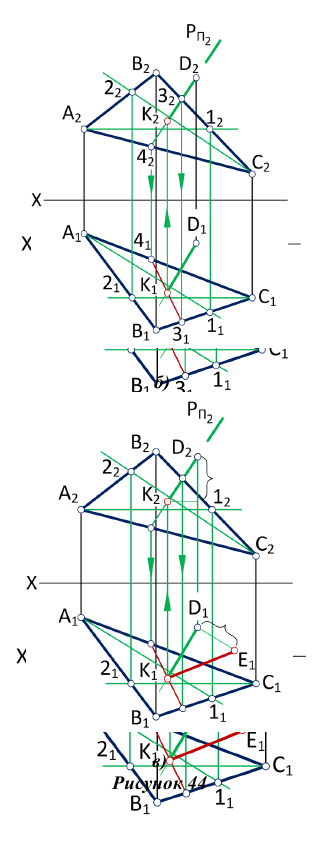
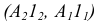
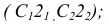
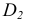
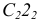
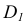
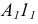
1. Из точки D опускаем перпендикуляр на плоскость треугольника AВС (рис.44, а), для этого в плоскости треугольника проводим горизонталь и фронталь затем из точки опускаем перпендикуляр на — получаем фронтальную проекцию перпендикуляра; а из точки -на — получаем горизонтальную проекцию перпендикуляра к плоскости

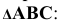
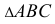
2. Находим точку пересечения перпендикуляра с плоскостью заключаем перпендикуляр во вспомогательную секущую плоскость Р; строим линию пересечения плоскости с плоскостью Р; определяем искомую точку К в пересечении перпендикуляра и построенной линии пересечения 3-4 (рис. 44,6).

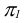
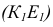
3. Методом прямоугольного треугольника определяем натуральную величину отрезка DK, для чего в плоскости (рис. 44,в) строим прямоугольный треугольник один катет которого является горизонтальной проекций перпендикуляра, а второй равен разности высот точек D и К. Гипотенуза построенного треугольника определяет искомое расстояние от точки D до плоскости треугольника ABC.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник