Что значит переместительное свойство
Переместительное свойство умножения – определение (5 класс, математика)
Переместительное свойство умножения очень похоже по своей сути на такое же свойство умножения. Тем не менее, часто ученики 5 класса, которые полностью овладели свойствами сложения, допускают ошибку в таких же по сложности законах умножения. Чтобы избежать этого разберемся подробнее в теме вопроса.
Что такое умножение?
Умножение это сокращенное сложение, базовые элементы которого принято знать наизусть. Под базовыми элементами понимается таблица умножения. Под упрощенным сложением имеется в виду то, что первый множитель показывает число, а второй сколько раз это число было сложено с самим собой.
В математике 3 ступени подобных упрощений. На первой стоит сложение, на второй умножение, а третьей возведение в степень. Возведение в степень это умножение числа на себя самого какое-то количество раз. Сколько раз нужно повторить умножение отражает показатель степени.
Закон или свойство?
Для того, чтобы не путаться, нужно разобраться, как правильно называть законы умножения. Законами или все же свойствами?
Проблема в том, что закон это непреложное правило, а свойство это некоторая особенность действия. И то, и другое верно для свойств умножения. Поэтому никакой разницы в названиях нет. Но принято говорить свойства сложения и законы умножения. Однако ошибкой не будет назвать свойства сложения законами сложения и наоборот.
Свойства умножения
Переместительное свойство гласит, от перемены мест множителей произведение не меняется.
Распределительное свойство может применяться и относительно вычитания или деления. С помощью этого свойства раскрывают скобки в примерах при необходимости.
Переместительное свойство
Правильное использование определения переместительного свойства умножения может увеличить скорость счета. К сожалению, специальных правил группировки нет. Нужно полагаться только на собственный опыт и логику. Рассмотрим небольшой пример, чтобы показать применение свойства на практике:
((15*25*7*3:125)-3):12 – в этом примере упростить можно только правильно сгруппировав произведение в скобках для ускорения деления. Для этого представим число 15 в виде произведения 3*5
((15*25*7*3:125)-3):12=((5*3*25*7*3:125)-3):12 теперь перемножим 5 и 25, выполним деление произведения на число. Для этого можно только один из множителей разделить на это число, а потом результат использовать, как один из множителей.
Без переместительного свойства не удалось бы правильно сгруппировать множители, а значит пришлось бы считать пример полностью, что отняло бы большое количество времени.
Что мы узнали?
Мы поговорили о том, что такое умножение. Решили, что понятия свойств и законов умножения одинаковы. Выделили свойства умножения и рассмотрели примеры переместительного свойства умножения. Сказали об особенностях этого свойства и его практическом значении.
Умножение натуральных чисел: свойства, примеры
Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.
Переместительное свойство умножения натуральных чисел
Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:
Переместительный закон умножения
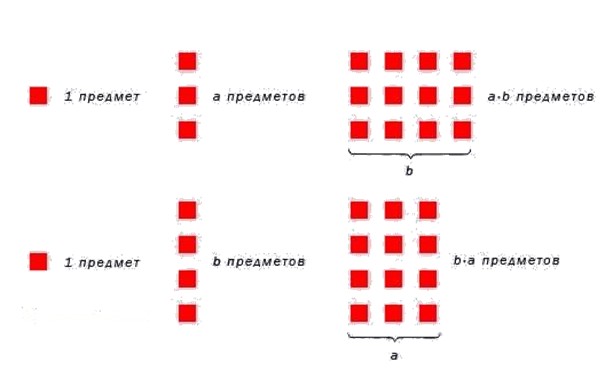
От перемены мест множителей произведение не меняется.
В буквенном виде переместительное свойство записывается так: a · b = b · a
На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.
Сочетательное свойство умножения натуральных чисел
Сочетательный закон умножения
Приведем формулировку в буквенном виде:
4 · 3 · 2 = 4 · 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24
4 · 3 · 2 = 12 · 2 = 12 + 12 = 24
Как видим, теория совпадает с практикой, и свойство справедливо.
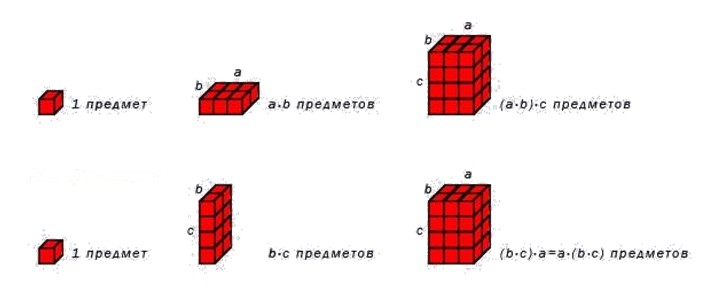
Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.
Распределительное свойство относительно умножения
Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.
Распределительное свойство умножения относительно сложения
Запишем в форме буквенного выражения:
a · b + c = a · b + a · c
4 · 3 + 2 = 4 · 3 + 4 · 2 = 12 + 8 = 20
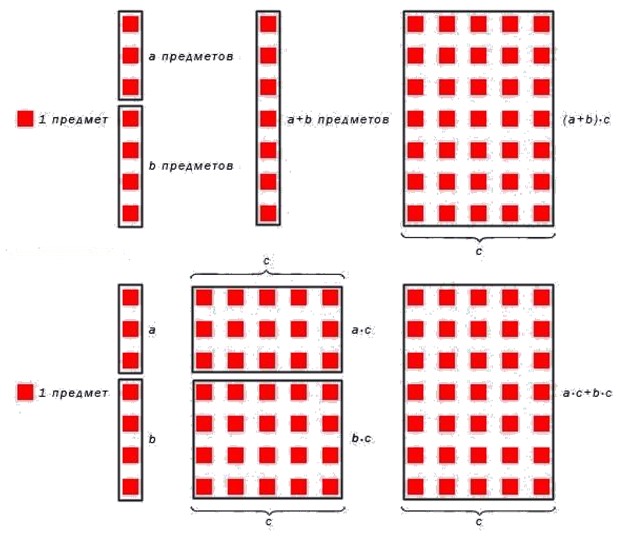
Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.
Распределительное свойство умножения относительно вычитания
Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.
Распределительное свойство умножения относительно вычитания
Запишем в форме буквенного выражения:
В предыдущем примере заменим «плюс» на «минус» и запишем:
Умножение единицы на натуральное число
Умножение единицы на любое натуральное число в результате дает данное число.
По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.
Умножение нуля на натуральное число
Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.
Умножение нуля на натуральное число
По определению, произведение 0 · a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.
В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.
Напимер: 0 · 498 = 0 ; 0 · 9638854785885 = 0
Свойства умножения чисел с примерами
В данной публикации мы рассмотрим 4 основных свойства умножения натуральных чисел, сопроводив их примерами для лучшего понимания теоретического материала.
Свойства умножения чисел
Свойство 1: переместительный закон
От перестановки мест сомножителей их произведение не меняется.
Примеры:
Примечание: количество сомножителей может быть любым. Например, вот произведение трех чисел:
Свойство 2: сочетательный закон
Результат умножения одного числа на произведение других (например, второго и третьего) равен произведению первого и второго числа, умноженному на третье.
Т.е. соседние (и не только) сомножители (их может быть любое количество) можно заменять их произведением.
Примеры:
Свойство 3: распределительный закон
Умножение на сумму чисел
Для умножения числа на сумму требуется это число отдельно умножить на каждое слагаемое, затем полученные результаты сложить.
a ⋅ (b + с) = a ⋅ b + a ⋅ c
Сомножители можно поменять местами (согласно переместительному свойству, рассмотренному выше):
(b + с) ⋅ a = a ⋅ b + a ⋅ c
Умножение на разность чисел
Чтобы число умножить на разность, нужно его отдельно умножить на уменьшаемое и вычитаемое, затем из первого результата вычесть второе.
a ⋅ (b – с) = a ⋅ b – a ⋅ c
Меняем сомножители местами и получаем:
(b – с) ⋅ a = a ⋅ b – a ⋅ c
Свойство 4: умножение на ноль
Если число (произведение чисел) умножить на ноль, в результате получится ноль.
Примеры:
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 16. Свойства сложения. Применение переместительного и сочетательного свойств сложения
Перечень вопросов, рассматриваемых в теме:
— Что такое сочетательное свойство сложения?
-В каких случаях можно использовать свойства сложения?
Переместительное свойство сложения: слагаемые можно переставлять местами, при этом значение суммы не изменится.
Сочетательное свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.44-47
2. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций/ Глаголева Ю.И., Волкова А.Д.-М.: Просвещение, Учлит, 2017, с.18, 19
3. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.- с.28, 29
Теоретический материал для самостоятельного изучения
Сравним выражения и их значения:
Сумма чисел шесть и девять равна сумме чисел девять и шесть.
Сумма чисел сорок пять и пять равна сумме чисел пять и сорок пять.
Значения выражений равны, так как от перестановки слагаемых значение суммы не меняется. Вспомним, как в математике называется данное свойство сложения?
Правильно, оно называется переместительным свойством сложения.
В школьном спортзале 3 волейбольных мяча, 5 баскетбольных мячей и 4 футбольных мяча. Сколько всего мячей в спортзале?
Первый способ решения.
Сначала узнаем, сколько волейбольных и баскетбольных мячей, затем прибавим число футбольных мячей. Запишем: к сумме чисел три и пять прибавить четыре, получится двенадцать.
Второй способ решения.
Прибавим к числу волейбольных мячей сумму баскетбольных и футбольных мячей. Запишем: к трем прибавить сумму чисел пять и четыре равно двенадцать.
В обоих случаях получили одинаковый результат, значит, выражения равны между собой. Можем записать так: (3+5)+4=3+(5+4)
Теперь ты знаешь еще одно свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой. Это свойство называется сочетательным свойством сложения.
Знание этих двух свойств сложения позволит нам решать примеры на сложение удобным способом.
Решим выражение: 1+7+9+3=?
Мы знаем, что слагаемые можно менять местами и соседние слагаемые заменять их суммой. Воспользуемся свойствами сложения и найдем сумму.
В данном случае удобно сложить попарно 1 и 9, 7 и 3. А затем сложить полученные результаты. Получим 20.
Делаем вывод: используя переместительное и сочетательное свойства сложения можно складывать числа в любом порядке, как удобнее.
1. Вычислите суммы удобным способом
30 + 3 + 7 + 40 = _________ 4 + 10 + 6 + 70=_______________
1. 30 + 3 + 7 + 40 = (3+7)+(30+40)=80 2. 4 + 10 + 6 + 70= (10+70)+(4+6)
2. Совместите название математического свойства с его значением и выражением
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
Переместительное свойство умножения

Всего получено оценок: 69.
Всего получено оценок: 69.
Переместительное свойство умножения очень похоже по своей сути на такое же свойство умножения. Тем не менее, часто ученики 5 класса, которые полностью овладели свойствами сложения, допускают ошибку в таких же по сложности законах умножения. Чтобы избежать этого разберемся подробнее в теме вопроса.
Что такое умножение?
Умножение это сокращенное сложение, базовые элементы которого принято знать наизусть. Под базовыми элементами понимается таблица умножения. Под упрощенным сложением имеется в виду то, что первый множитель показывает число, а второй сколько раз это число было сложено с самим собой.
В математике 3 ступени подобных упрощений. На первой стоит сложение, на второй умножение, а третьей возведение в степень. Возведение в степень это умножение числа на себя самого какое-то количество раз. Сколько раз нужно повторить умножение отражает показатель степени.
Закон или свойство?
Для того, чтобы не путаться, нужно разобраться, как правильно называть законы умножения. Законами или все же свойствами?
Свойства умножения
Распределительное свойство может применяться и относительно вычитания или деления. С помощью этого свойства раскрывают скобки в примерах при необходимости.
Переместительное свойство
Правильное использование определения переместительного свойства умножения может увеличить скорость счета. К сожалению, специальных правил группировки нет. Нужно полагаться только на собственный опыт и логику. Рассмотрим небольшой пример, чтобы показать применение свойства на практике:
((15*25*7*3:125)-3):12 – в этом примере упростить можно только правильно сгруппировав произведение в скобках для ускорения деления. Для этого представим число 15 в виде произведения 3*5
((15*25*7*3:125)-3):12=((5*3*25*7*3:125)-3):12 теперь перемножим 5 и 25, выполним деление произведения на число. Для этого можно только один из множителей разделить на это число, а потом результат использовать, как один из множителей.
Без переместительного свойства не удалось бы правильно сгруппировать множители, а значит пришлось бы считать пример полностью, что отняло бы большое количество времени.
Что мы узнали?
Мы поговорили о том, что такое умножение. Решили, что понятия свойств и законов умножения одинаковы. Выделили свойства умножения и рассмотрели примеры переместительного свойства умножения. Сказали об особенностях этого свойства и его практическом значении.