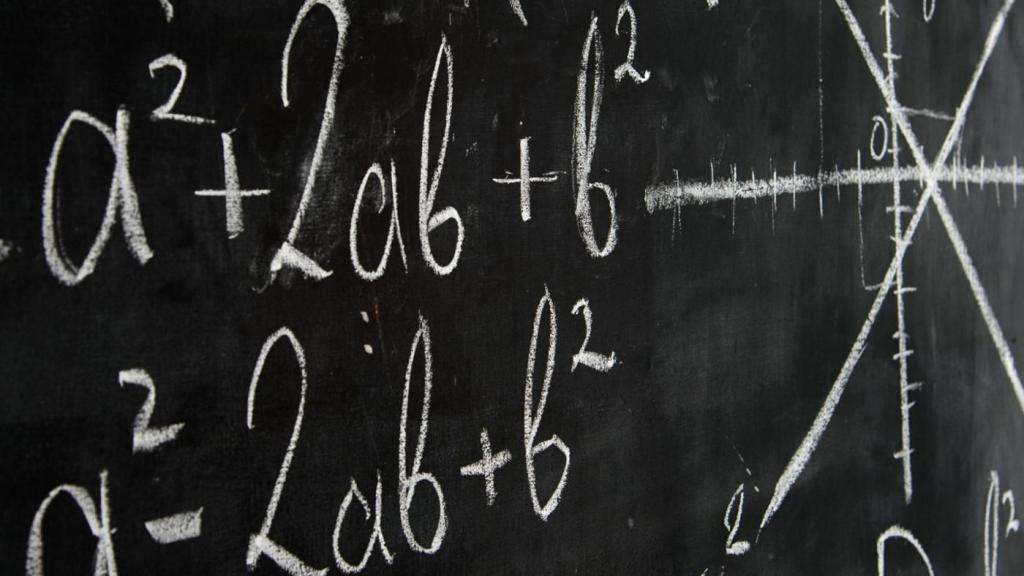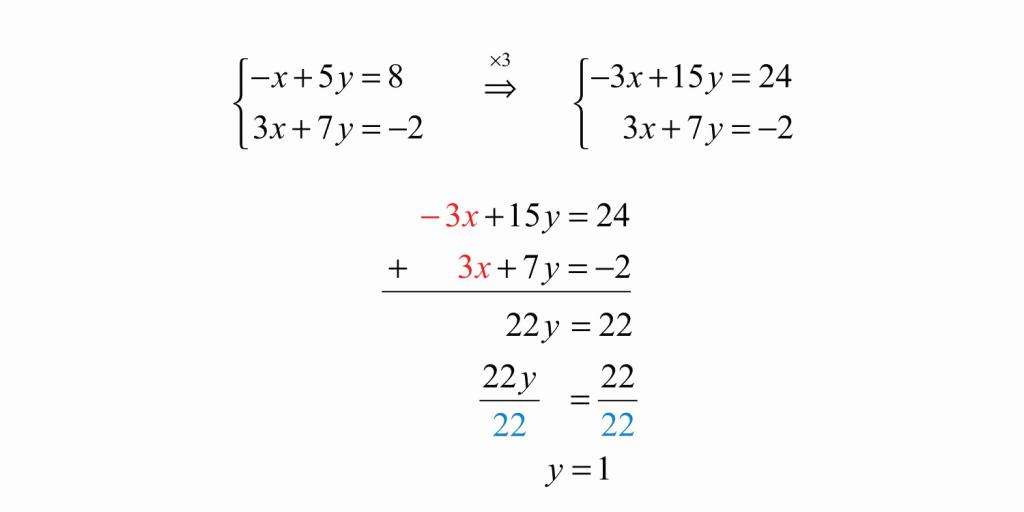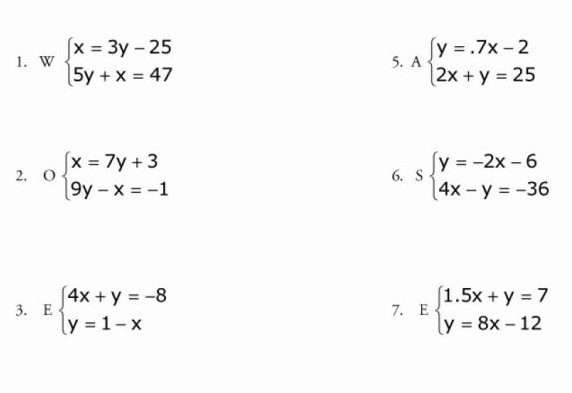Что значит переменная в математике 6 класс

что такое переменная в математике?

Переме́нная — атрибут физической или абстрактной системы, который может изменить свое значение. Примеры переменных: рост ребёнка, температура в воздуха, или параметр функции.

Концепция переменной широко используется в таких областях как математика, естественные науки и техника

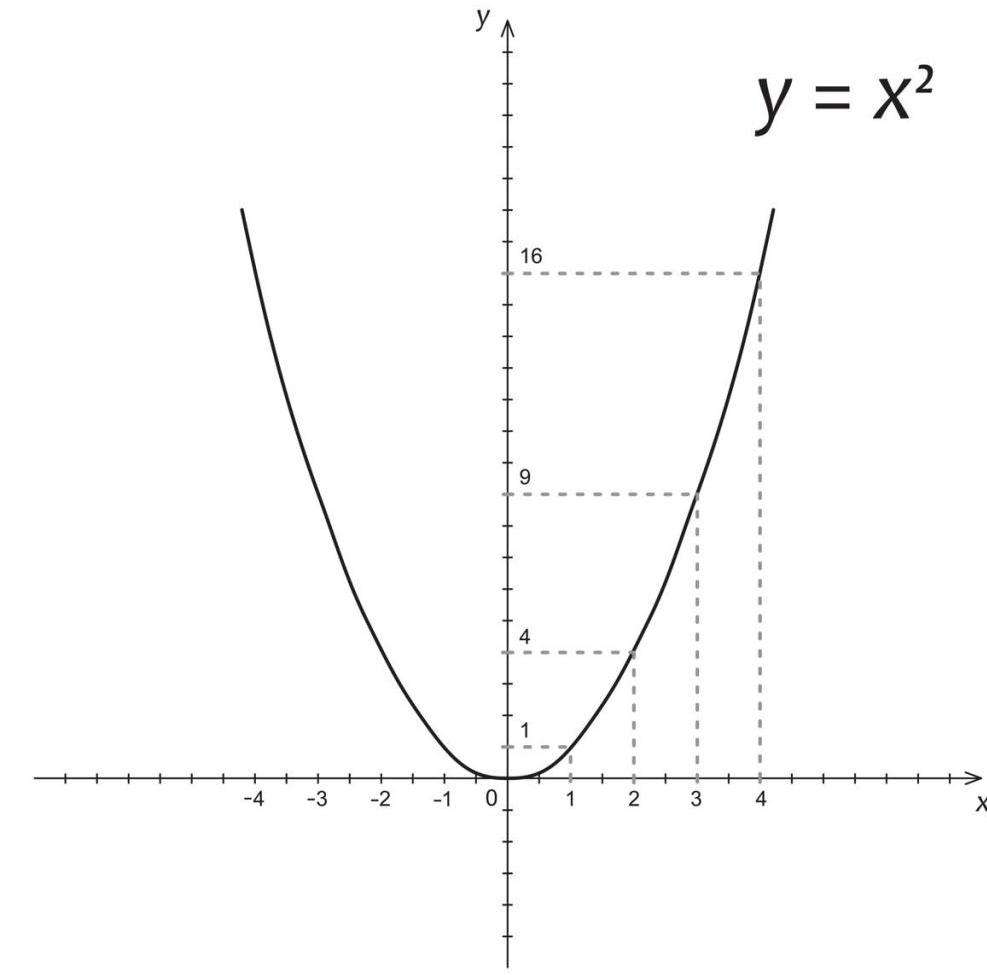
В области математики и компьютерных наук, переменные, как правило, обозначаются одним или несколькими словами или символами, такие, как «time» или «x». В математике, новичков часто смущает то, что букву «x» иногда используется для обозначения переменной, как и в выражение y = x2, а иногда и для обозначения неизвестного как в выражении 2x = 6.

При моделировании, переменные необходимо отличать от параметров, несмотря то, что переменная в одном контексте может быть параметром в другом.

В прикладной статистике, переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами

В математике переменная — это величина, характеризующаяся множеством значений, которое она может принимать.

[1] При этом может иметься в виду как реальная физическая величина, временно рассматриваемая в отрыве от своего физического контекста, так и некая абстрактная величина, не имеющая никаких аналогов в реальном мире. В математическом анализе и большинстве смежных разделов математики под «переменной» обычно понимают численную величину, множество принимаемых значений которой включено в множество вещественных чисел.
Множество всех значений, которые может принимать данная переменная, называется областью изменения этой переменной.

Это множество и задаёт переменную, то есть формально и является ей.
При моделировании переменные необходимо отличать от параметров, несмотря на то что переменная в одном контексте может быть параметром в другом.

В прикладной статистике переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами.

В математике переменной может быть как реальная физическая величина, так и некая абстрактная величина, не отражающая процессов реального мира.

В математическом анализе и большинстве смежных разделов математики под переменной x понимают каждый элемент некоторого множества, состоящего, например, из вещественных чисел. Фиксированный элемент этого множества — число называется значением переменной. Само множество называется областью изменения переменной.

Источник

Что значит переменная в математике 6 класс

Единое национальное тестирование

История Казахстана

Онлайн тесты и шпаргалки по истории Казахстана

Всемирная история

Онлайн тесты и шпаргалки по Всемирной истории.

Математика

Онлайн тесты и шпаргалки по математике.

Химия

Онлайн тесты и шпаргалки по химии.

Физика

Онлайн тесты и шпаргалки по физике.

Биология

Онлайн тесты и шпаргалки по биологии.

География

Онлайн тесты и шпаргалки по географии.

Русский язык

Онлайн тесты и шпаргалки по русскому языку.

Готовые работы

ДИПЛОМНЫЕ РАБОТЫ

КУРСОВЫЕ РАБОТЫ

МАГИСТЕРСКИЕ ДИССЕРТАЦИИ

ОТЧЕТЫ ПО ПРАКТИКЕ

После прохождения любого типа студенческой практики (учебной, производственной, преддипломной) требуется составить отчёт. Этот документ будет подтверждением практической работы студента и основой формирования оценки за практику. Обычно, чтобы составить отчёт по практике, требуется собрать и проанализировать информацию о предприятии, рассмотреть структуру и распорядок работы организации, в которой проходится практика, составить календарный план и описать свою практическую деятельность.
Мы поможет написать отчёт о прохождении практики с учетом специфики деятельности конкретного предприятия.

Новости сайта

Обучение по государственному образовательному заказу (магистратура)

Комплексное тестирование проводилось с 3 по 7 декабря текущего года. 10 декабря текущего года текущего года начинается прием заявлений для участия в конкурсе по присуждению государственных образовательных грантов на подготовку магистров.

Для участия в конкурсе на присуждение государственного образовательного гранта на подготовку магистров поступающий до 18:00 часов (по местному времени) 14 декабря подает заявление через виртуальную приемную комиссию любой организации высшего и послевузовского образования (далее – ОВПО). Поступающие в магистратуру в заявлении указывают одну группу образовательных программ и до 3-х (трех) ОВПО.

На обучение по государственному образовательному заказу на конкурсной основе зачисляются лица, набравшие наивысшие баллы по КТ и (или) вступительному экзамену и (или) творческих экзаменов: 1) для научно-педагогической магистратуры с казахским или русским языком обучения, в том числе по группам образовательных программ, требующих творческой подготовки, по группам образовательных программ, требующих знания арабского языка – не менее 75 баллов; 2) для профильной магистратуры с английским или с казахским или русским языком обучения – не менее 50 баллов.

Источник

Что такое переменная величина в математике

Содержание статьи

Переменные

Основным показателем переменной является то, что она записывается не числом, а буквой. Под условным обозначением чаще всего скрывается определенное значение. Переменная получила свое название благодаря тому, что ее значение меняется в зависимости от уравнения. Как правило, любая буква алфавита может быть использована в качестве обозначения для такого элемента. Например, если вы знаете, что у вас есть 5 рублей и вы хотите купить яблоки, которые стоят 35 копеек, конечное количество яблок, которые можно купить, обозначается буквой (например «С»).

Пример использования

Если есть переменная, которая была выбрана по вашему усмотрению, необходимо составить алгебраическое уравнение. Оно будет связывать между собой известные и неизвестные величины, а также показывать связь между ними. Это выражение будет включать в себя цифры, переменные и одну алгебраическую операцию. Важно отметить, что выражение будет содержать знак равенства.

Полное уравнение содержит значение выражения в целом. Оно отделено от остального уравнения знаком равенства. В предыдущем примере с яблоками 0.35 или 35 копеек, умноженные на «С», является выражением. Для того чтобы создать полное уравнение, необходимо записать следующее:

Мономиальные выражения

Полиномы

Зависимые и независимые переменные

В математике независимыми переменными являются неизвестные, которые определяют другие части уравнения. Они стоят отдельно в выражениях и не изменяются вместе с другими переменными.

Значения зависимых переменных определяются с помощью независимых. Их значения зачастую определяются эмпирически.

Источник

Что такое переменные? Переменная величина в математике

Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.

Понятие переменной

Вам будет интересно: Плотность осмия: характеристика, значение, физические и химические свойства, получение и применение

Вам будет интересно: Российская таможенная академия в Москве: описание, адрес, факультеты.

Виды величин

Вам будет интересно: Конспект урока русского языка во 2 классе. Правила «жи – ши», «ча – ща», «чу – щу»

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).

Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.

С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:

За x2 принимаем некое k, и уравнение приобретает понятный вид:

Вот какую пользу в математику несет введение переменных.

Неравенства, примеры решения

Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Вам будет интересно: Французские местоимения: типы и виды

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

Пример с одной переменной:

Делим обе части неравенства на 10 и получаем:

Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.

Квадратные неравенства

Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

По формуле корней квадратного уравнения получаем:

Или можно было решить это уравнение по теореме Виета:

Методом подбора получаем такие же корни уравнения.

Парабола

1. Определяем, куда направлены ветви параболы.

2. Приравниваем функцию к нулю и находим корни уравнения.

3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.

Выписываем в виде функции:

Приравниваем к нулю.

Дальше решаем как квадратное уравнение и находим нули функции:

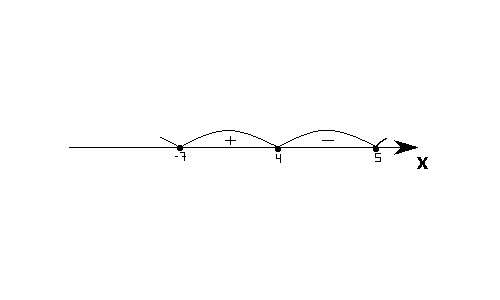
Метод интервалов

1. Находим корни уравнения, при которых неравенство равно нулю.

2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.

3. Определяем знак любого интервала.

4. Расставляем знаки у остальных интервалов, меняя их через один.

2) Изображаем их на числовой прямой.

3) Определяем знаки интервалов.

2. Отмечаем их на числовой прямой.

3. Определяем знаки интервалов.

Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.

Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.

Системы уравнений

Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.

Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.

Алгебраический метод

Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.

Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:

Решаем получившееся уравнение и находим икс.

Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:

Метод подстановки

Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.

В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:

Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:

Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:

Источник

Урок по математике 6 класс «Понятие переменной. Выражения с переменными»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Сценарии уроков по учебнику «Математика, 6 класс», часть 1

Тема: «Понятие переменной. Выражения с переменной».

1) тренировать способность к составлению выражений с переменными, нахождению их значений при данном значении переменной;

2) тренировать способность к рефлексии собственной деятельности;

3) повторить и закрепить перевод десятичной дроби в обыкновенную дробь и обратно, простые задачи на дроби и проценты.

1) самостоятельная работа № 1.

2. Длина прямоугольника равна 1,2 см, а ширина b см. На сколько периметр квадрата со стороной равной ширине прямоугольника, меньше периметра прямоугольника? Составьте выражение с переменной и найдите его значение при b = 0,3.

После выполнения работы учащиеся проводят самопроверку по образцу и фиксируют правильность выполнения работы в тетрадях и таблице.

2) подробный образец выполнения самостоятельной работы № 1.

Если p = 0,6, y = 3,1, то 0,3 : 0,6 × 3,1 = 0,5 × 3,1 = 1,55.

3) эталон для самопроверки самостоятельной работы № 1.

1. x : y = 0,3 : p Чтобы найти значение x, можно:

1 способ выразить из равенства x, как неизвестное делимое: значение частного умножить на делитель x = 0,3 : p × y ;

теперь найдём значение, подставив вместо переменных р и y данные значения:

Если p = 0,6, y = 3,1, то 0,3 : 0,6 × 3,1 = 0,5 × 3,1 = 1,55.

2 способ подставим в данное равенство значение переменных р и y: x : 3,1 = 0,3 : 0,6.

Найдём значение частного в правой части равенства: x : 3,1 = 0,5.

(1,2 + b ) × 2 – периметр прямоугольника;

на сколько периметр прямоугольника больше периметра квадрата.

В данное выражение подставим значение переменной b =0,3

4) алгоритм исправления ошибок (Урок – 6)

5) дополнительные задания.

6) подробное решение дополнительных заданий.

Дать рисунок графика.

Дать рисунок графика.

7) самостоятельная работа № 2.

2. Длина прямоугольника равна 2,1 см, а ширина x см. На сколько периметр квадрата со стороной равной ширине прямоугольника, меньше периметра прямоугольника? Составьте выражение с переменной и найдите его значение при x = 0,2.

8) эталон для самопроверки самостоятельной работы № 2.

1. Если а = 4,2, с = 5, то 0,5 : 5 × 4,2 = 0,1 × 4,2 = 0,42. Чтобы найти значение x, можно:

1 способ выразить из равенства x, как неизвестное делимое: значение частного умножить на делитель x = 0,5 : с × а;

теперь найдём значение, подставив вместо переменных с и а данные значения

x : 4,2 = 0,5 : 5; 2 способ подставим в данное равенство значение переменных с и а.

x : 4,2 = 0,1. Найдём значение частного в правой части равенства.

x = 0,1 × 4,2; Найдём неизвестное делимое.

4 × x– периметр квадрата;

на сколько периметр прямоугольника больше периметра квадрата.

В данное выражение подставим значение переменной x=0,2

9) задание для выбора.

Ответ: 1) (а + а : 0,4) × 2 (11,5 м); 2) с : b ( ); 3) V : ( d × 0,3 d ) (2,5 м); 4) n × 1,5 n × 0,24 × 2,5 n (7,2 м 3 ).

10) таблица фиксации результатов.

Исправлено в ходе работы над ошибками

Исправлено по результатам второй самостоятельной работы по эталону

11) карточка для этапа рефлексии.

1) У меня сегодня всё получалось, я не допускал ошибок;

2) Я допустил ошибки в первой самостоятельной работе (перечислить ошибки);

3) Я исправил допущенные ошибки в процессе работы над ними;

4) Я не смог самостоятельно исправить ошибки, но исправил их с помощью эталона;

5) Я без ошибок справился со второй самостоятельной работой;

6) Во второй самостоятельной работе я допустил ошибки (перечислить их);

7) Я выполнил дополнительное задание (перечислить выполненные номера);

8) В дополнительном задании я допустил ошибки (перечислить их);

9) Мне необходимо поработать над…

1. Самоопределение к деятельности.

Цель этапа: включить учащихся в учебную деятельность, определить содержательные

рамки урока: использование понятия переменной.

Организация учебного процесса этапа 1:

– Какую тему мы начали изучать на прошлом уроке? (Переменная и выражения с переменными.)

– Где мы использовали понятие переменной? (В буквенных выражения, в уравнениях, в формулах.)

– Сегодня на уроке мы продолжим работать с понятием переменная и с выражениями с переменной.

2. Актуализация знаний и фиксация затруднений в деятельности.

Цель этапа: актуализировать знания о составлении буквенных выражениях, нахождения значений числовых и буквенных выражений при данных значениях букв, порядка действий; выполнить самостоятельную работу; зафиксировать задания, вызвавшие затруднение.

Организация учебного процесса этапа 2:

1. Найдётся ли прямоугольник, стороны которого выражаются натуральными числами, а периметр, которого, есть простое число? (Нет, т.к. P = ( a + b ) × 2, значит периметр всегда чётное число, не равное 2, а значит, составное.)

2. Периметр прямоугольника x см. Выбери из данного ряда числа, которым может равняться x : 144; 37; 114; 125; 84. (144; 104; 84.)

3. Назовите верные значения x в порядке возрастания: (84; 114; 144.)

– Установите закономерность и продолжите ряд на три числа вперёд. (84; 114; 144; 174; 204; 234, каждое следующее число на 30 больше предыдущего.)

– Какое число, по вашему мнению, в данном ряду чисел является «лишним»? (Основания для выбора «лишнего» числа у учащихся могут быть различные, к примеру: число 84 может быть «лишним», так как оно двузначное, а все остальные числа однозначные, или число 144 может быть «лишним», так как цифра 4 содержится в этом числе не только в разряде единиц, но и в разряде десятков, а в остальных числах цифра 4 содержится только в разряде единиц, и т.д.)

– Найдите в данном ряду квадрат числа 12. (144).

– Верно ли утверждение, что сумма цифр натурального числа равна сумме цифр квадрата этого числа? Докажите примерами. (Не верно, например: 11: 1 + 1 = 2; 11 × 11 = 121: 1 + 2 + 1 = 4.)

– Чем отличается формула нахождения периметра прямоугольника от нахождения периметра квадрата? (Чтобы найти периметр квадрата надо его сторону умножить на 4, т.к. все стороны квадрата равны.)

– Сейчас вы будете выполнять самостоятельную работу.

Перед выполнением самостоятельной работы случаи возможных затруднений фиксируются на доске и индивидуально:

Учащиеся выполняют самостоятельную работу, на работу отводится 5 минут.

Перед проверкой работ:

— Что необходимо проверить прежде, чем проверять работу по образцу? (Необходимо проверить, что задание списано правильно.)

— Какой следующий шаг? (Проверить задание по образцу и зафиксировать результат.)

По мере проверки учащиеся фиксируют несовпадения с предъявленным образцом и заполняют второй столбец своей таблицы. Если задание выполнено точно так же, как на образце, то в таблице против соответствующего номера они ставятся знак «+», а если есть расхождения, то фиксируют их знаком «?».

3. Локализация затруднения.

Цель этапа: указать место в задании, где допущена ошибка, определить правило, в котором допущена ошибка, уточнить цель урока.

Организация учебного процесса этапа 3:

— Если у вас все ответы совпали с образцом, что вам необходимо сделать? (Проверить свою работу по эталону для самопроверки и можно приступать к дополнительному заданию.)

Тем учащимся, у которых совпали все результаты, предлагается проверить свою работу по эталону для самопроверки и дополнительные задания: №№ 78, 80.

С теми учащими, которые допустили ошибки организовать диалог по локализации затруднения.

— Какой следующий шаг вы должны сделать после проверки работы и фиксации результатов? (Надо найти место ошибки и понять её причину.)

— Что нужно сделать для этого? (Постараться подробно расписать задание, если это не сделано при выполнении работы.)

— Каков может быть результат такой работы? (Можем получить правильный ответ или опять получить не правильный ответ.)

— Если ответ не совпал с образцом, что необходимо сделать? (Определить, какие правила необходимо использовать при выполнении задания и повторить эти правила.)

–Какую цель вы ставите для себя на этом уроке? (Определить причину ошибки и исправить её.)

— Что необходимо сделать после того, как вы повторите правила, на которые вы допустили ошибку? (Надо попробовать исправить ошибку и придумать аналогичное задание и решить его.)

— Если при исправлении вы опять получаете неправильный ответ? (Надо обратиться к эталону и разобраться в причине ошибки по нему и исправить её, а затем придумать аналогичное задание и решить ег.о)

— Что вам поможет выполнить работу над ошибками? (Алгоритм исправления ошибок).

— Перед вами лежит схема выхода из затруднения, которое мы сейчас уточнили, эта схема поможет вам выполнить работу над ошибками.

4. Построение проекта выхода из затруднения.

Цель этапа: уточнить способы действий, в которых допущены ошибки; исправить ошибки на основе правильного применения правил; придумать или выбрать из предложенных заданий на способы действий, в которых допущены ошибки.

Организация учебного процесса этапа 4:

Учащиеся самостоятельно выполняют работу над ошибками, учитель на данном этапе выступает в качестве консультанта. Если им удаётся самостоятельно исправить ошибку, они заполняют четвёртый столбик таблицы. По окончании работы учащиеся получают эталоны и ещё раз анализируют свою работу, им предлагается придумать и выполнить задание аналогичное тому, в котором была допущена ошибка.

5. Обобщение причин затруднений во внешней речи.

Цель этапа: зафиксировать в речи правила, в которых были допущены ошибки.

Организация учебного процесса этапа 5:

Учитель последовательно выясняет у кого из детей, на какие правила были допущены ошибки и правила проговариваются во внешней речи. В этой работе могут принять участие все учащиеся.

6. Самостоятельная работа с самопроверкой по эталону.

Цель этапа: проверяем способность к выполнению заданий, которые на предыдущей самостоятельной работе вызвали затруднение; сопоставить полученное решение с эталоном для самопроверки.

Организация учебного процесса этапа 6:

Выполните вторую самостоятельную работу.

Работа проверяется по эталону для самопроверки.

Пока учащиеся выполняют вторую самостоятельную работу, первая группа детей проверяют дополнительные задания по подробному образцу.

7. Включение в систему знаний и повторение.

Цель этапа: тренировать навыки перевода десятичных дробей в обыкновенные дроби, алгоритм действий с обыкновенными дробями, тренировать навыки перевода обыкновенных дробей в десятичные дроби, алгоритм действий с десятичными дробями.

Организация учебного процесса этапа 7:

1) ; 3) ; 5) ;

2) ; 4) ; 6) ;

7) ; 8) .

1) 0,8 + 0,2 = 1; 3) 3,75 – 0,25 = 3,5; 5) 0,52 × 11,111 = 5,77772;

2) 0,5 + 2,3 = 2,8; 4) 5,125 – 3,125 = 2; 6) 2,002 дробь нельзя перевести в десятичную дробь.

7) 0,36 : 0,036 = 10; 8) 70,707 : 0,14 = 505,05.

8. Рефлексия деятельности.

Цель этапа: зафиксировать, где были допущены ошибки, способ исправления допущенных ошибок; зафиксировать содержание, которое повторили на уроке, оценить собственную деятельность; записать домашнее задание.

Организация учебного процесса этапа 8.

– Какую тему мы сегодня повторяли? (Понятие переменной.)

– В чём испытали затруднение?

– Что помогло выйти из затруднения?

– Над чем необходимо ещё поработать?

– Проанализируйте свою работу на уроке.

Домашнее задание : задания для выбора; №№ 93, 95 (2).

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник