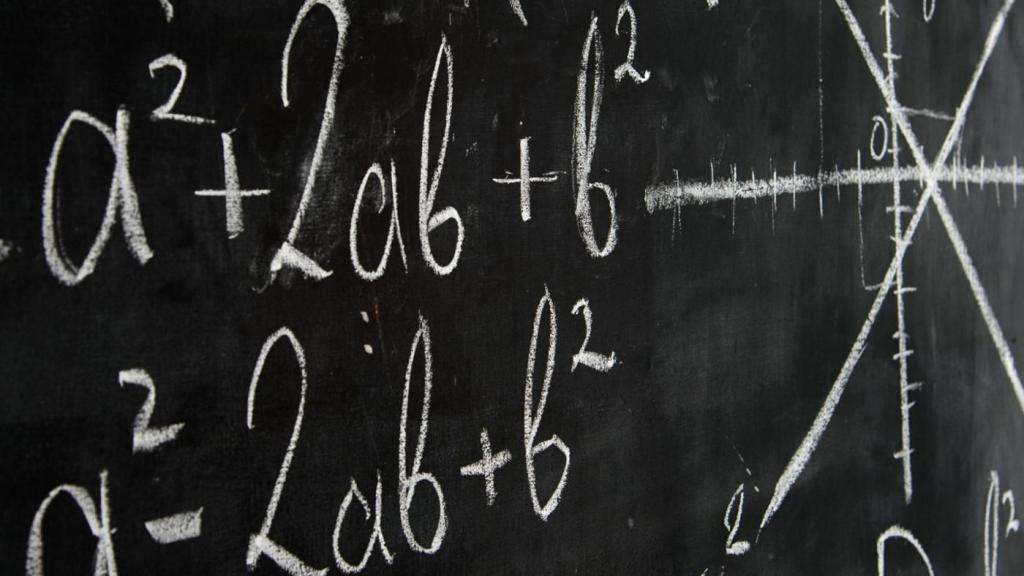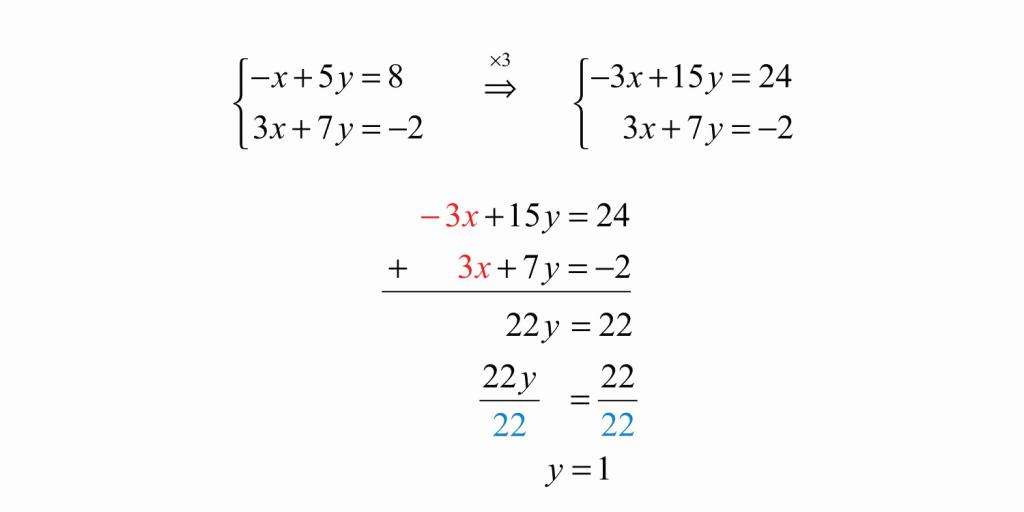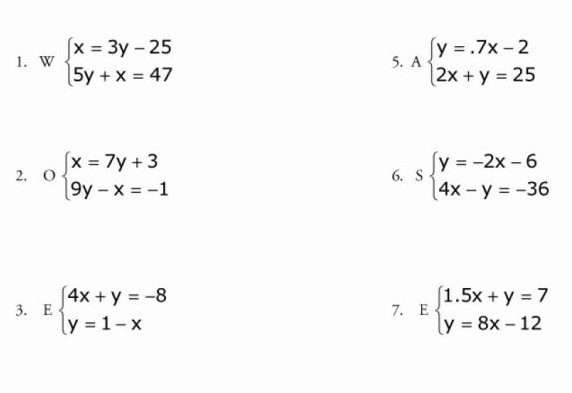Что значит переменная в алгебре 7 класс

Что такое переменная величина в математике

Содержание статьи

Переменные

Основным показателем переменной является то, что она записывается не числом, а буквой. Под условным обозначением чаще всего скрывается определенное значение. Переменная получила свое название благодаря тому, что ее значение меняется в зависимости от уравнения. Как правило, любая буква алфавита может быть использована в качестве обозначения для такого элемента. Например, если вы знаете, что у вас есть 5 рублей и вы хотите купить яблоки, которые стоят 35 копеек, конечное количество яблок, которые можно купить, обозначается буквой (например «С»).

Пример использования

Если есть переменная, которая была выбрана по вашему усмотрению, необходимо составить алгебраическое уравнение. Оно будет связывать между собой известные и неизвестные величины, а также показывать связь между ними. Это выражение будет включать в себя цифры, переменные и одну алгебраическую операцию. Важно отметить, что выражение будет содержать знак равенства.

Полное уравнение содержит значение выражения в целом. Оно отделено от остального уравнения знаком равенства. В предыдущем примере с яблоками 0.35 или 35 копеек, умноженные на «С», является выражением. Для того чтобы создать полное уравнение, необходимо записать следующее:

Мономиальные выражения

Полиномы

Зависимые и независимые переменные

В математике независимыми переменными являются неизвестные, которые определяют другие части уравнения. Они стоят отдельно в выражениях и не изменяются вместе с другими переменными.

Значения зависимых переменных определяются с помощью независимых. Их значения зачастую определяются эмпирически.

Источник

Что означает переменная в математике?

Тем не менее, каково количество членов в алгебраическом выражении?

Каждое выражение состоит из терминов. Термин может быть числом со знаком, переменной или константой, умноженной на переменную или переменные. Каждый член в алгебраическом выражении отделяется знаком + или J. Условия: 5x, 3y и 8. … В члене 5x коэффициент равен 5.

далее, какие 3 типа переменных?

тогда, что такое переменный пример?

Сколько терминов в выражении?

Как найти термины в последовательности?

Какие 5 переменных?

Как вы объясняете переменные студентам?

Какая переменная должна оставаться постоянной?

Переменная в эксперименте, которая поддерживается постоянной для оценки взаимосвязи между несколькими переменными, является управляющая переменная.

Какие бывают 5 типа переменных?

Какие бывают 4 типа переменных?

Четыре типа переменных

Как видите, существует четыре различных типа шкал измерения (номинальный, порядковый, интервальный и коэффициент). Каждая из четырех шкал, соответственно, обычно предоставляет больше информации об измеряемых переменных, чем предыдущие.

Что такое переменная в 2х?

Какие термины используются в выражении?

Срок: каждое выражение состоит из терминов. Термин может быть числом со знаком, переменной или константой, умноженной на переменную или переменные. Фактор: что-то, что умножается на что-то еще. Фактор может быть числом, переменной, термином или более длинным выражением.

Как называется термин без переменной в алгебраическом выражении?

Что означает 3x в математике?

3x это коэффициент с переменной x. Например: 3x + 4. X3 должно означать x с показателем 3.

Что такое формула ряда?

Серия последовательности сумма последовательности к определенному количеству членов. Его часто пишут как S_n. Итак, если последовательность 2, 4, 6, 8, 10,…, сумма до 3 членов = S₃ = 2 + 4 + 6 = 12.

Как найти следующие четыре члена последовательности?

Переменная называется непрерывной, если она может принимать бесконечное количество действительных значений. Примеры непрерывная переменная расстояние, возраст и температура.

Сколько существует типов переменных?

Существуют

три типа

категориальных переменных: двоичных, номинальных и порядковых переменных.

Как объяснить, что такое переменная?

Что делают переменные при кодировании?

Какая ключевая переменная?

A общая переменная между двумя наборами данных, которые, следовательно, могут использоваться для связывания записей между ними. Ключевая переменная может быть формальным идентификатором или квазиидентификатором.

Что такое пример постоянной переменной?

TL; DR: В научном эксперименте контролируемая или постоянная переменная переменная, которая не меняется. Например, в эксперименте по проверке воздействия различных источников света на растения необходимо, чтобы другие факторы, влияющие на рост и здоровье растений, такие как качество почвы и полив, оставались постоянными.

Как вы контролируете переменную в статистике?

Переменные могут быть контролируются напрямую, поддерживая их постоянными на протяжении всего исследования (например, контролируя комнатную температуру в эксперименте), или ими можно управлять косвенно с помощью таких методов, как рандомизация или статистический контроль (например, для учета характеристик участников, таких как возраст, в статистических тестах).

Как узнать, постоянна ли переменная?

число перед алфавитом (переменная) называется константой. Переменная: символ, который принимает различные числовые значения, называется переменной. Алфавит после числа (константы) называется переменной.

Источник

Что такое переменные? Переменная величина в математике

Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.

Понятие переменной

Вам будет интересно: Плотность осмия: характеристика, значение, физические и химические свойства, получение и применение

Вам будет интересно: Российская таможенная академия в Москве: описание, адрес, факультеты.

Виды величин

Вам будет интересно: Конспект урока русского языка во 2 классе. Правила «жи – ши», «ча – ща», «чу – щу»

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).

Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.

С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:

За x2 принимаем некое k, и уравнение приобретает понятный вид:

Вот какую пользу в математику несет введение переменных.

Неравенства, примеры решения

Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Вам будет интересно: Французские местоимения: типы и виды

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

Пример с одной переменной:

Делим обе части неравенства на 10 и получаем:

Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.

Квадратные неравенства

Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

По формуле корней квадратного уравнения получаем:

Или можно было решить это уравнение по теореме Виета:

Методом подбора получаем такие же корни уравнения.

Парабола

1. Определяем, куда направлены ветви параболы.

2. Приравниваем функцию к нулю и находим корни уравнения.

3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.

Выписываем в виде функции:

Приравниваем к нулю.

Дальше решаем как квадратное уравнение и находим нули функции:

Метод интервалов

1. Находим корни уравнения, при которых неравенство равно нулю.

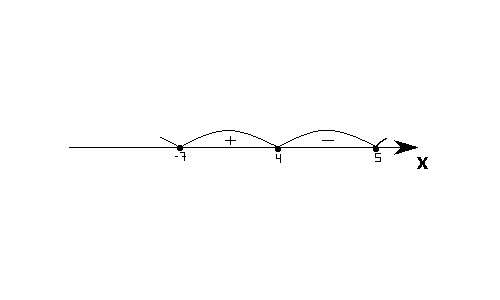
2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.

3. Определяем знак любого интервала.

4. Расставляем знаки у остальных интервалов, меняя их через один.

2) Изображаем их на числовой прямой.

3) Определяем знаки интервалов.

2. Отмечаем их на числовой прямой.

3. Определяем знаки интервалов.

Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.

Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.

Системы уравнений

Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.

Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.

Алгебраический метод

Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.

Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:

Решаем получившееся уравнение и находим икс.

Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:

Метод подстановки

Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.

В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:

Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:

Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:

Источник

2. Выражения с переменными

Двигаясь со скоростью 60 км/ч, автомобиль за 2 ч пройдёт 60 • 2 км, за 3 ч — 60 • 3 км, за 5 ч — 60-5 км, за 5,5 ч — 60 • 5,5 км. Вообще за t ч он пройдёт 60t км. Изменяя значение t, мы можем с помощью выражения 60t находить путь, пройденный автомобилем за разные промежутки времени. Для этого достаточно вместо буквы t подставить её значение и выполнить умножение. Букву t в выражении 60t называют переменной, а само выражение 60t — виражением с переменной.

Если в выражение с переменными подставить вместо каждой переменной какое-либо её значение, то получится числовое выражение. Его значение называют значением вы ражения с переменными при выбранных значениях переменных.

Так, число 88 есть значение выражения ab при a = 8 и b = 11, число 100 есть значение этого выражения при а = 25 и b = 4.

Рассмотрим выражение . При любом b ≠ 3 можно найти его значение. Например, если b = 13, то .

Некоторые выражения имеют смысл нри всех значениях переменных. Примерами могут служить выражения

Выражения с переменными используются для записи формул.

Любое чётное число m можно представить в виде произведения числа 2 и целого числа n, т. е.

Если в эту формулу вместо n подставлять целые числа, то значениями переменной m будут чётные числа. Формулу m = 2n называют формулой чётного числа.

Формулу m = 2n + 1, где n — целое число, называют формулой нечётного числа.

Аналогично формуле чётного числа можно записать формулу числа, кратного любому другому натуральному числу.

Например, формулу числа, кратного 3, можно записать так: m = Зn, где n — целое число.

а) кратного 5; б) кратного 10; в) кратного 101.

а) 3% этого числа равны 1,8;

б) 85% этого числа равны 17;

в) 130% этого числа равны 3,9;

Источник

Функция. Зависимые и независимые переменные. Область определения и область значений функции.

теория по математике 📈 функции

Определение понятия функции. Переменные.

Зависимость переменной у от переменной х, при которой любому значению переменной х соответствует единственное значение переменной у, называют функцией.

Ключевое слово, которое нужно запомнить в определении функции – это зависимость.

Например, человек идет на деловую встречу, но чувствует, что он опаздывает. Он ускоряет свой шаг, потому что от его скорости зависит время. Чем быстрее он двигается, тем меньше времени уйдет у него на дорогу. То есть время зависит от скорости.

Или, например, спортсмен метает ядро на дальнее расстояние. Чем сильнее будет бросок, тем дальше полетит ядро. Скорость полета зависит от силы толчка. Здесь опять прослеживается зависимость.

Например, функция задана формулой у = – 3х 2 – 7. Равносильная ей запись такая: f(x)= – 3х 2 – 7.

Области определения и значения функции

Все возможные значения независимой переменной (х) называют областью определения функции.

Все значения, которые принимает зависимая переменная (у) называют областью значений функции.

Если какая-либо функция у=f(x) задана формулой, а при этом ее область определения не указана, то считается, что она состоит из любых значений переменной, при которых выражение имеет смысл.

Области определения и значений школьных функций

1. Для линейной функции областью определения будет являться любое число.

Если у такой функции k≠0, то областью ее значений также будет являться любое число.

При k=0 область значений этой функции состоит из единственного числа b.

Например, функция задана формулой у = 7. Тогда ее область значения — это число 7, а область определения – любое число.

2. Гипербола задается формулой вида y = k/x.

Область определения такой функции – любое число, кроме нуля.

Область значений такой функции – аналогичная.

3. Функция, заданная формулой y= |x|, имеет область определения – любое число.

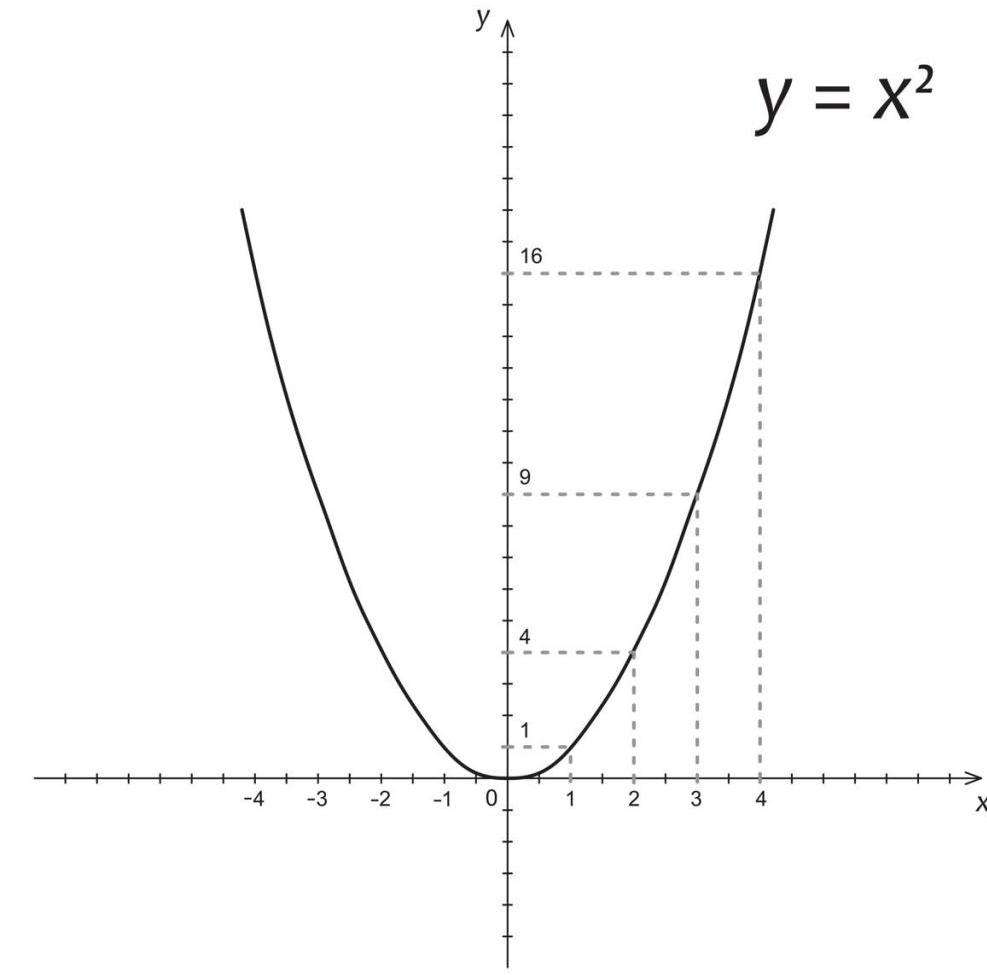
4. У функций у = х 2 и у = х 3 область определения – любое число.

Для того чтобы понимать, как находится область определения функции и рассмотреть примеры заданий на нахождение области определения функции, вспомним правила, при которых существуют ограничения и выражение не имеет смысл: нельзя делить на нуль; нельзя извлекать квадратный корень из отрицательного числа.

Пример 3. Рассмотрим, как находится область определения функций, которые заданы следующими формулами:

В знаменателе этого выражения содержится переменная х, поэтому надо проверить, при каком значении он может быть равным нулю и исключить это значение из области определения, так как на знаменатель делят, а на нуль делить нельзя.

Итак, имеем знаменатель х + 11. Приравниваем его к нулю, получаем х + 11 = 0. Решаем простое уравнение на нахождение неизвестного слагаемого и получаем х= – 11. Это число исключаем из области определения функции.

Ответ: (1) и (2) – множество всех чисел; (3) – любое число, кроме (-11) или х ≠ – 11; (4) х ≥0.

Источник