Что значит переход через десяток
Счет в пределах 20
Изучение чисел до 20 выделяется в особый этап. На этом этапе важно помочь ребенку понять новую счетную единицу — десяток и объяснить, как образуются числительные второго десятка.
В основе всех чисел второго десятка лежит понятие десятка.
Нужно, чтобы ребенок хорошо понял, то десять кубиков и один десяток кубиков обозначают одно и то же.
Для этого задаем вопросы: «Сколько здесь кубиков? А сколько десятков кубиков?» С помощью кубиков можно показать, как образовались названия чисел второго десятка.
Таким образом, можно показать образование всех чисел второго десятка.
Сложение и вычитание без перехода через десяток
Также рассуждаем при вычитании. Пример:
Сложение с переходом через десяток
Чтобы сложить однозначные числа с переходом через десяток нужно соблюдать следующий порядок действий.
Рассмотрим это на примерах:
Сделаем это письменно.
Рассмотрим другой пример.

Вычитание с переходом через десяток
Чтобы вычесть однозначное число из двузначного с переходом через десяток соблюдаем следующий порядок действий.
Рассмотрим следующий пример:
Рассмотрим еще один пример.
Счет через десяток: подсказки для первоклашки для лучшего запоминания
Все первоклашки мучаются, изучая счет через десяток, вроде 5+7 или 16-8.
Увы, никакого волшебного средства для запоминания этого счета нет – только зубрёжка.
По крайней мере, я не нашла. Если знаете – буду благодарна за комментарий
Для Шурки я придумала несколько «подсказок», которые помогают запомнить некоторые примеры с переходом через десяток.
Поделюсь с вами. Может, кому-то что-то из этого пригодится.
Единицы в уменьшаемом и вычитаемом идут подряд в порядке убывания. Значит в ответе будет на 1 десяток меньше и всегда 9 единиц
В ответе будет на 1 десяток меньше, на 1 единицу больше
На 1 меньше, чем прибавить 10-ку
На 1 меньше, чем прибавить 9-ку
Остальные примеры на сложение
Остается выучить совсем мало примеров на сложение:
Я выбрала 5+7 и сказала: «Спорим, ты никогда не запомнишь ответ?»
И Сашка запомнил «на слабо». Всё остальное он из этого списка он может посчитать, отталкиваясь от 5+7:
Если 5+7=12, то 6+7=13 (на одну больше), а 6+6=12 (на одну меньше, чем 6+7)
С вычитанием сложнее
Здесь чаще всего Сашка пользуется вопросом.
Допустим 15-8. Он спрашивает себя: «Сколько надо прибавить к 8, чтобы получилось 15? Или сколько восьмёрке не хватает до 15и?»
И дальше применяет либо «подсказку», либо запомненные «сложные случаи».
Еще он любит вычитать через десяток через отрицательные числа – сам придумал этот способ. Позже я расскажу, как он это делает. Как по мне – просто фантастика, я бы не додумалась ))))
Всё это звучит долго, но на самом деле у него получается очень быстро.
И, да, конечно, лучше – зазубрить наизусть. Но если зазубрить пока не получается, то – мне кажется – не плохой способ.
А запоминание придет обязательно, рано или поздно, никуда не денется ))
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Посмотри ты на игрушки:
Мишки,куклы и хлопушки,
Только некогда играть,
Пора урок наш начинать!
Правда, играть с игрушками веселее, чем учиться? Но это не всегда так! Сегодня на уроке мы отправимся в магазин игрушек. Мы немножко поиграем, но, главное, научимся решать очень сложные примеры. Это будут примеры на вычитание.
Ты уже знаешь, что это за математическое действие. Вспомни, что значит вычитание? Правильно, вычитание обозначает удаление из множества предметов их части. При этом предметов остается меньше.
Подумай, чем мы будем заниматься в магазине, чтобы на математическом языке наши действия можно было описать вычитанием. Совершенно верно, мы будем продавать игрушки. Надеюсь, ты умеешь считать деньги. Давай проверим. Назови число, которое ты видишь на монете.,
Правильно, это 10 рублей.
А теперь посмотри на другие монеты. Назови их.
Подумай, как с помощью этих монет можно заменить 10 рублей.
Правильно, вот самый простой способ.
Ведь десять – это пять и пять.
А вот еще один вариант.
Посмотри, как я разделю монеты на две группы. Скажи, сколько рублей получилось в каждой группе.
Получается, что десять – это семь и три.
Назови следующую комбинацию.
Если ты правильно посчитал, то у тебя получилось, что десять – это девять и один.
А как разделились монеты здесь?
Верно, десять – это шесть и четыре.
Ну и посчитай еще один вариант.
Все правильно. Десять – это восемь и два.
Пересмотри еще раз все способы, как мы раскладывали монеты и заодно хорошо повтори состав числа 10. Как только ты это сделаешь, мы приступим к изучению нового материала.
Общие приёмы табличного вычитания с переходом через десяток
Сегодня мы рассмотрим несколько приемов вычитания с переходом через десяток. Ты можешь из них выбрать тот, который позволит тебе быстро и правильно находить результаты вычислений в математических выражениях.
Первый способ основан на связи действий сложения и вычитания. На прошлом уроке мы выучили все таблицы сложения с переходом через десяток. Давай разберемся, как ты можешь использовать знание примеров из этой таблицы для выполнения действия вычитания.
Вот как нужно рассуждать, чтобы решить пример:
Вот и все. Если хорошо знаешь таблицы сложения с переходом через десяток, то соответствующие таблицы вычитания даже и учить не придется.
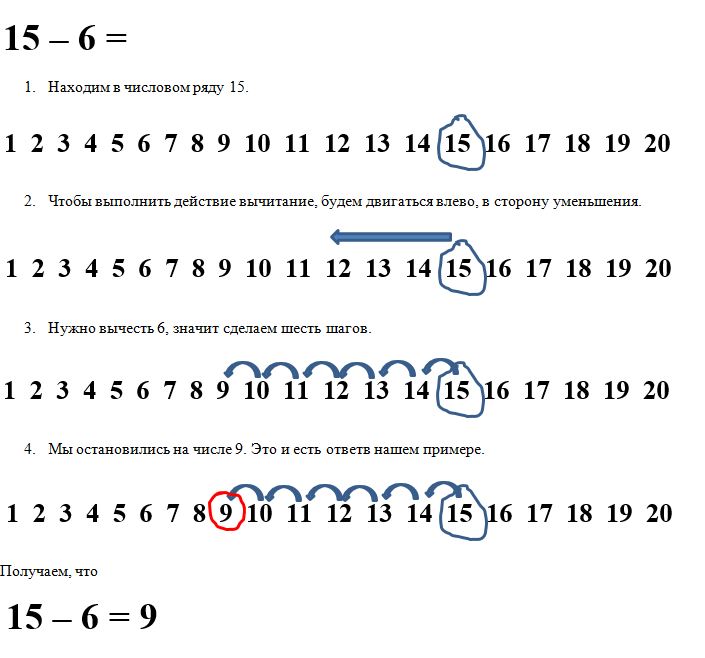
Второй способ мы позаимствуем из урока, на котором изучали табличное сложение и вычитание в пределах 10. Вспомнил? Мы находили результат с помощью героев из сказки «Теремок», которые передвигались по числовому ряду.
Вот как можно решать примеры таким способом.
Для выполнения вычитания таким способом можно использовать линейку.
Третий способ является основным для вычитания с переходом через десяток. Предлагаю подробно с ним разобраться.
Заглянем в наш магазин. Он не обычный, а математический. В этом магазине на полках помещается ровно десять игрушек, т.е. целый десяток.
Итак, у нас на полках стоят машинки. Посчитай, сколько их.
Обрати внимание, как расставлены машинки.
10 на одной полке и 4 на другой.
Для детского сада нужно продать 6 машинок.
Начнем снимать машинки с нижней полки. Сколько это будет машинок?
Правильно, только 4. Сколько после этого останется машинок на полках?
Совершенно верно, останется ровно 10.
Нам нужно снять еще несколько машинок.
Мы должны продать 6 машинок, а мы взяли только 4. Сколько еще надо достать?
Верно, еще 2 машинки, ведь 6 это 4 и 2. Мы их возьмем с верхней полке, на которой оставалось 10 машинок. Сколько там останется машинок?
Итак, останется 8 машинок.
Давай теперь все наши действия запишем в виде математического выражения.
Такой прием называется вычитание по частям. Выполняется он в такой последовательности.
Этот прием вычитания с переходом через десяток очень похож на соответствующий прием сложения. Рассмотрим и закрепим его, составляя таблицы вычитания.
Начнем с таблицы вычитания вида 11- □. Составим первый пример.
У нас на полках было 11 мишек.
Сегодня мы продали 2 медвежонка. Составим пример.
Мне кажется, что все легко и понятно.
Прежде чем мы начнем решать следующие примеры, предлагаю немного поиграть. Но игра будет познавательная! В нашем магазине есть математическое домино.,
Ты знаешь эту игру. В ней используются специальные карточки, разделенные на две половинки. Нам такие карточки помогут вспоминать состав чисел, чтобы мы могли быстро и без ошибок представлять вычитаемое в виде пары удобных чисел.
Смотри, как нам нужно это делать. В следующем примере вычитаемым будет 3. Значит на нашей карточке всего должно быть три кружочка. В левой половине мы нарисуем один кружок.
Если ты затрудняешься с ответом при последнем вычитании, вспоминай состав числа 10, который мы повторили, раскладывая монетки. 10 это 2 и 8. Значит, когда мы из 10 вычитаем 2, у нас остается 8.
Все понятно? Тогда мы можем продолжать.
Рассмотрим следующий пример.
Перед тем как продолжить, предлагаю еще поиграть. Ты любишь кататься на качелях? В нашем магазине есть вот такая качелька.
Знаешь, как на ней кататься? Давай усадим на эти качели числа. Например, компоненты из нашего последнего примера.
А число 11 будет их раскачивать. Когда 6 поднимается вверх –5 опускается вниз.
А потом наоборот. 5 взлетает, а 6 опускается вниз.
В математике тоже есть такие «качели». Если из 11 вычесть 5 – получим 6, а если из 11 вычесть 6 – получим 5. Вот так, все легко и просто. Вторую часть таблицы ты можешь сам составить всего за пару минут. Покачайся на математических качелях и запиши примеры – перевертыши.
Посмотри, что должно получиться.
Ты прекрасно справился. Заметил, что учить наизусть нужно только половину таблицы? Правда, здорово?
Перейдем к составлению следующей таблицы. В ней примеры на вычитание вида 12- □. Поэтому мы начнем с анализа уменьшаемого.
На полках стояло 12 пирамидок.
На картинке хорошо виден разрядный состав числа 12. В нем 1 десяток и 2 единицы. Вот мы и получили первое число, которое должно входить в состав вычитаемого – это 2.
Подружки купили 3 пирамидки. Вот какой получится пример.
Продолжим вычитание с уменьшаемым 12.
Определиться с составом числа 5 нам поможет домино с пятью кружочками. Слева должно быть два кружочка. Тогда справа нужно дорисовать третий, четвертый и пятый кружок.
Итак, посмотрим, какие примеры мы решили.
Хорошо их запомни. Так тебе будет легче составлять остальную часть таблицы. Помнишь, как мы катались на качелях? Давай и сейчас сделаем тоже. Кстати, перед тем как решать примеры, можешь выполнить небольшую физминутку: несколько раз приседай и поднимайся на носочки.
Если ты уже отдохнул, то приступай. Проверь свои результаты.
К нам в магазин забежали мальчишки. Они увидели на полках самолетики. Посмотри на картинку. Сколько их.
Правильно, у нас 13 самолетиков. Значит мы будем составлять таблицу вычитания числа 13. Ты уже по рисунку можешь определить разрядный состав уменьшаемого 13 и узнать, сколько мы будем вычитать сначала, чтобы осталось 10.
Да, это вычитаемое 3.
Итак, рассмотрим наш первый пример.
Постарайся запомнить все примеры.
Дальше мы будем составлять таблицу вычитания вида 14— □. У нас в магазине есть 14 симпатичных куколок. Ты догадался, как мы их расставим на полках? Посмотри.
Сразу видно, что 14 это 10 и 4, т.е. в числе 14 всего 4 единицы. Поэтому сначала будем вычитать 4. Итак приступим.
Для детского праздника у нас купили 5 куколок. Составим пример.
Исследуем состав числа 7. Можешь вспомнить нужный вариант? Если затрудняешься, то давай опять вернемся к игре в домино.
Слева должно быть четыре кружочка. Досчитай остальные справа: пять, шесть, семь.
Ты любишь роботов? В нашем магазине их много. Сосчитай.
Верно, их 15. А это значит, что мы будем работать над составлением таблицы вычитания вида 15— □. За день мы продали 6 роботов! Это любимая игрушка для всех мальчиков. Давай узнаем, сколько роботов осталось в магазине.
Мы рассмотрели все случаи вычитания вида 15- □. Перейдем к следующей таблице.
Ни в одном магазине игрушек не обойтись без мячиков. Есть они и у нас. Посчитай.
Если на второй полке 6 мячей, значит всего их 16. Ведь 16 = 10 + 6.
На центральных полках у нас стоят наборы конструкторов. Посчитал? Здесь 17 наборов.
Сегодня мы продали их больше всего. Целых 9 наборов.
У нас получится такой пример.
Уверена, что у тебя все получилось. Значит ты хорошо усвоил основной прием табличного вычитания с переходом через десяток – вычитание частями. Со временем ты запомнишь все рассмотренные примеры из наших таблицы.
Я собрала их все в общую таблицу вычитания.
Хорошенько заучи примеры. Скоро ты будешь учиться находить значение математических выражений с большими числами. Без знания нашей таблицы ты не сможешь справиться с ними.
Тренируйся, пока у тебя не получится с первого разу выполнить все тестовые задания правильно.
Счет с переходом через десяток, счет во втором десятке (счет от 10 до 20), часть 2
Во второй части статьи мы рассмотрим некоторые способы сложения и вычитания с переходом через десяток.
В начале приведем все варианты примеров сложения, которые предстоит освоить ребенку:
9 + 2 9 + 3 9 + 4 9 + 5 9 + 6 9 + 7 9 + 8 9 + 9
8 + 3 8 + 4 8 + 5 8 + 6 8 + 7 8 + 8
7 + 4 7 + 5 7 + 6 7 + 7
У взрослых может возникнуть резонный вопрос: почему в приведенной таблице первое слагаемое всегда больше или равно второму и почему отсутствуют остальные варианты примеров? Скажем, 3 + 9, 5 + 8 и т.п. Для ответа укажем два важных правила, которые должен запомнить ребенок:
Правило №1: от перестановки мест слагаемых сумма не меняется.
Правило №2: обычно легче к большому числу прибавить маленькое, чем наоборот, к маленькому прибавить большое.
Рекомендуем Вам распечатать или переписать от руки приведенную таблицу и вычеркивать в ней решенные примеры, а также отмечать, в решении каких примеров возникли трудности.
Вначале научимся решать пример из первой строки: прибавление к 9 чисел от 2 до 9. Отметим здесь, что существуют разные формы объяснения и записи решения подобных примеров в разных учебниках по математике.
Приведем некоторые варианты:
Мы будем использовать вторую форму записи.
Какое объяснение можно дать ребенку для примера 9 + 4?
«Ты понимаешь, что к девяти палочкам нам нужно добавить четыре. Давай подумаем, сколько палочек нужно добавить к девяти, чтобы получить число десять? Конечно, одну палочку. Если мы должны были добавить четыре палочки, а уже добавили одну, значит нам остается добавить еще три палочки. И ответ будет: тринадцать. Посмотри, как мы запишем то, что мы сделали»:
Предложите ребенку еще несколько примеров из верхней строки таблицы (9 + n).
После того, как ребенок начнет решать подобные примеры самостоятельно, можно переходить к примерам второй строки таблицы (8 + n).
После усвоения решения подобных примеров, переходим к третьей строке таблицы
(7 + n).
После того, как ребенок решит несколько примеров типа 7 + n, предложите ребенку самостоятельно решить примеры 6 + 5 и 6 + 6. Если у него это не получается – помогите.
Можно предложить ребенку попробовать обобщить свой опыт (выразить его в общем виде). Как надо выполнять сложение с переходом через десяток либо выучить правило из учебника по математике.
В дальнейшем рекомендуем Вам предложить ребенку выучит следующие примеры:
Если ребенок выучит хотя бы эти суммы, он легко сможет решать примеры типа:
6 + 5, 7 + 6, 8 + 7, 9 + 8. В этих случаях одно из слагаемых отличается на единицу от уже знакомых вариантов.
Но: 6 + 6 = 12, значит 7 + 6 = 13 (и одно слагаемое и сумма увеличились на единицу).
В перспективе ребенку предстоит выучить все правильные ответы для всех сочетаний слагаемых, но, конечно же, он должен уметь перепроверить, правильную ли сумму он указывает.
Как объяснить ребенку вычитание во втором десятке?
«Ты понимаешь, что мы должны удалить 3 палочки из 11. Сначала мы убираем одну единичную палочку. Затем нам надо развязать пучок из 10 палочек и убрать еще 2 палочки, останется: 10 – 2 = 8 палочек.»
Как это записать математически:
Аналогично решаем примеры 11 – n, 12 – n, и т.д. до 19 – n.
Приводим здесь решение некоторых примеров:
После того, как первоклассник научится считать подобные примеры, возможно дать выучить правила в общем виде.
Если ребенок запомнил суммы для примеров 6 + 6, 7 + 7, 8 + 8, 9 + 9, то он это может использовать при вычитании, т.к.
6 + 6 = 12, то 12 – 6 = 6, а 13 – 6 = 7.
Если уменьшаемое увеличилось на 1, то и разность увеличится на 1, т.к.
7 + 7 = 14, то 14 – 7 = 7, а 15 – 7 = 8 и т.п.
В дальнейшем постарайтесь мотивировать ребенка к тому, чтобы он выучил все варианты сумм и разностей и легко мог их проверить.
Желаем Вам успехов в обучении Вашего ученика!
Как научить ребенка считать примеры в пределах 20
Итак, первые шаги в математической науке уже пройдены, и теперь родителям предстоит объяснить ребенку, как же складывать или вычитать числа в пределах 20-ти. Безусловно, самое главное в математике – понять все премудрости этой науки. Не подсмотреть у соседа по парте, не посчитать на палочках или пальцах (рук и ног), а именно понять, почему нужно поступать так, а не иначе.
Эта сложная наука – математика
Некоторым деткам научиться математическому счету бывает намного труднее, чем, например, научиться читать. Поэтому, чтобы у ребенка появилась так называемая «симпатия» к предмету, родителям придется постараться привить любовь ребенка к математике.
Некоторые родители не желают обременять себя подобными делами и перекладывают обучение вычислениям на плечи педагогов начальной школы. Безусловно, именно учителя и выполняют обучение счету детей, но родители не должны самоустраняться, а обязаны помогать ребенку, помогать находить ошибки, анализировать их.
Даже если вы решили воспользоваться услугами репетитора, заниматься с ребенком дома все равно придется, ведь учитель задает домашние задания, которые следует добросовестно выполнять. В противном случае знания, не подкрепленные практикой, очень быстро забудутся.
Как научить считать в пределах 20-ти
Педагоги с опытом рекомендуют использовать для объяснения азов вычитания и сложения в пределах второго десятка по уже разработанным алгоритмам. Это поможет детям понять и осмыслить, что представляет собой один и два десятка, как складывать числа или вычитать их, если они переваливает через десяток. Занимаясь с ребенком, каждый раз следует проверять, насколько хорошо он понял пройденный материал, закрепить его, и не перескакивать на следующие темы, если в предыдущей остались пробелы.
С чего начать?
Прежде всего ребенок должен знать, как называются числа второго десятка и в каком порядке они идут друг за другом. После этого понадобится двадцать одинаковых деталей чего-либо: кубиков, счетных палочек, карточек от игр и прочее.
Разложите с ребенком кубики (карточки, палочки и прочее) в два ряда по 10 штук в каждом ряду. Первый ряд – это первый десяток, можете даже пронумеровать все кубики первого десятка. Второй ряд – это числа второго десятка. Выложите их один под другим, т.е. кубики с порядковыми номера «один» и «одиннадцать» должны располагаться один над другим, «два» над «двенадцать», «пять» над «пятнадцать» и так далее.
Запоминать названия чисел второго десятка так будет намного проще: 11 – к слову «один» прибавляет окончание «-дцать», лежит на нем «один», так и получает «один-на-дцать». Таким же образом получаем и другие числа «две-на-дцать», «три-на-дцать» и так далее. Повторяйте с ребенком такое упражнение до тех пор, пока он не запомнит числа.
Вычисления без перехода через десяток
Перед тем, как начать обучение счету в пределах двух десятков, ребенок должен четко понимать, где у числа десятки, а где – единицы. Если вы будете объяснять ребенку правила вычисления «на пальцах», то скорее всего, он ничего не поймет. Для обучения вам потребуются наглядные пособия, например, кубики.
Чтобы объяснить ребенку, как делать вычисления без перехода через десяток, попросите его выложить в линию 10 кубиков. Это десяток. Теперь попросите его прибавить к ним еще 3 кубика, поставив их сверху на первые десяток (одиннадцатый кубик на первых, двенадцатый на второй, тринадцатый на третий). Проговаривайте свои действия – «десять плюс три равно тринадцать». Подобный образом составьте и другие числа, без перехода через десяток.
Примерами на сложение и вычитание без перехода через десяток считаются такие, в которых все математические действия совершаются с целым или целыми десятками и еще несколькими единицами.
Например:
10+5=15 16-6=10
10+8=18 17-10=7
После того, как ребенок поймет, как совершается сложение, можно переходить к примерам на вычитание. Если маленький школьник поймет принцип сложения и вычитания чисел до 20-ти, значит у него не будет проблем и с математическими действиями чисел второго, третьего десятка и так далее в пределах сотни.
Вычисления с переходом через десяток
Математические примеры на сложение и вычитание с переходом через десяток несколько сложнее, и поэтому ребенок долен быть готов к этому этапу обучения. Для этого ему необходимо выучить состав чисел первого десятка.
Например, состав числа 2 – то 1 и 1, а состав числа 3 – это две пары чисел: 2 и 1 или 1 и 2, а состав числа 5 – это следующие пары: 1 и 4, 2 и 3, 3 и 2, 4 и 1. И так для каждого числа первого десятка.
Для чего это необходимо? Выполняя арифметические действия ребенку придется сначала письменно, а затем и устно раскладывать прибавляемое или вычитаемое число так, чтобы оно дало десяток при сложении или вычитании с первым.
Вторым важным условием для перехода к этому этапу является быстрый устный счет в пределах первого десятка. Без этого, ребенку будет сложно удержать в голове видимые числа и те, на которые он раскладывает одно из видимых.
Рассмотрим на примере алгоритм решения примеров на сложение с переходом через десяток.
Нужно прибавить к 8 число 6.
8+6=
Запишем этот пример так:
8+(2+4) =
Т.е. мы раскладываем второе слагаемое 6 на два числа, чтобы в сумме с первым слагаемым 8 получить десятку. После того, как мы складываем 8 и 2 и получаем десятку, нам видно, что при добавлении к нему числа 4 мы получим число 14
Значит 8+(2+4) = 14 или 8+6 = 14
Для закрепления рассмотрим еще несколько примеров на сложение.
6+9 =
Этот пример можно записать следующим образом:
6+(4+5) = 15
Записываем его в таком виде:
7+(3+5) = 15
Рассмотрим на примере алгоритм решения примеров на вычитание с переходом через десяток.
Чтобы вычесть из одного числа другое с переходом через десятку, нужно разложить вычитаемое таким образом, чтобы у нас получилась десятка при первом отнимании.
В данном случае число 7 состоит из 5 и 2. Запишем этот пример так, чтобы в первом действии у нас получилась десятка
(15-5)-2 = 8
Ребенку легче будет решать такие примеры, если он запомнит, что при вычитании нужно раскладывать вычитаемое так, чтобы сразу же отнять у первого числа единицы.
Например:
14-6=
Раскладываем вычитаемое (6 состоит из 4 и 2)
(14-4)-2 = 8
16-9=
Раскладываем вычитаемое (9 состоит из 6 и 3)
(16-6)-3=7
Т.е. при вычитании какое бы число не нужно было разложить, сначала вычитаем единицы из первого числа, чтоб осталась десятка, а затем уже вычитаем оставшееся число.
Рекомендации родителям
Не стоит рассчитывать, что эти простые истины математики дадутся ребенку с легкостью. Даже если соседская девочка или сын сотрудницы освоил сложение и вычитание за один день, это не повод впадать в отчаяние. Во-первых, все дети разные и у всех индивидуальные особенности усвоения информации, а во-вторых, если кто-то что-то освоил быстрее, еще не значит, что учиться ему будет легче.
Кроме того, при обучении малыша родителям нужно следить за реакцией ребенка на это обучение. Если вы видите, что ему не интересно, попробуйте сменить тактику. Считайте конфеты, яблоки, книжки, можно вырезать одинаковые фигурки для обучения, а затем сделать из них праздничную гирлянду.
Если в определенный период времени ребенок отказывается учиться, у него плохое настроение или самочувствие, не настаивайте. Перенесите время урока на более благоприятный период. Зато у малыша не пропадет желание к учебе, как к чему-то неприятному и неизбежному. Ну и самое главное, проявляйте терпение к его стараниям и почаще хвалите. Для него это очень важно.