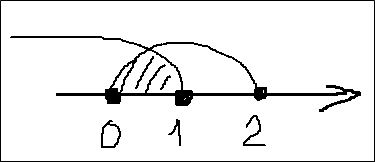Что значит перечеркнутый круг в математике
Как пересекать промежутки?
Операции над числовыми промежутками.
Операций над промежутками совсем немного. Всего две. Это пересечение и объединение. При решении серьёзных заданий с неравенствами эти две операции над промежутками необходимо проделывать постоянно. В самых разных сочетаниях. По своей сути это очень простые операции. Но, справедливости ради, эти самые операции являются вторым источником досадных ошибок при решении неравенств после тождественных преобразований. Разберёмся?
Пересекать и объединять числовые промежутки, проще всего при помощи числовой оси. Начнём с пересечения, оно хоть и проще в визуальном восприятии, но простора для ошибок даёт больше…
Как пересекать промежутки?
Сама по себе операция пересечения промежутков совсем простая. Тем не менее, именно пересечение промежутков — самая богатая на сюрпризы операция, которая столько людей ушибла! И очень больно ушибла. Но мы-то с вами — люди думающие и осторожные! С сюрпризами разберёмся, да и под ноги смотреть будем.) И не споткнёмся на ровном месте.
Итак, для начала запоминаем:
Пересечением двух числовых промежутков называется их общая часть.
И всё! Смутить могут только слова «общая часть». Всё просто. Общая часть — это те точки (или кусочки оси), которые одновременно входят в каждый из промежутков. Слова «общая часть» и «одновременно» здесь синонимы. Если раз и навсегда разобраться в этих нехитрых словах, то при ответе на любой вопрос о пересечении любых промежутков вы даже не заметите проблем! Намёк понятен?)
Возможно, вы до сих пор в сомнениях, но картинка с числовой осью, наш главный помощник, всё сразу же прояснит! Это только на конкретных примерах показать можно.
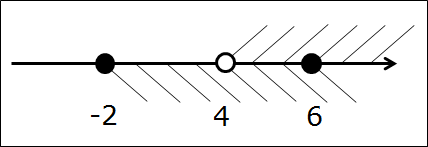
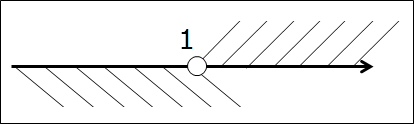
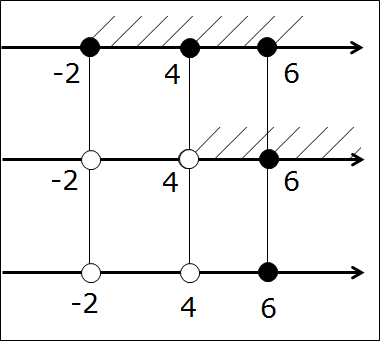
Начнём с совсем простенького, безо всяких подводных камней в виде выколотых точек. Допустим, нам надо пересечь два промежутка:
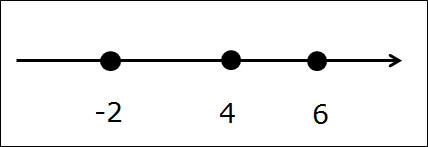
Первым делом рисуем числовую ось, отмечаем все граничные точки правильными кружочками. Они здесь — чёрные:
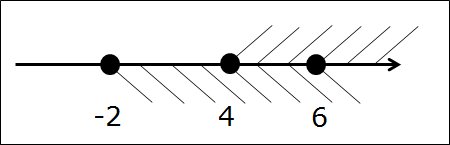
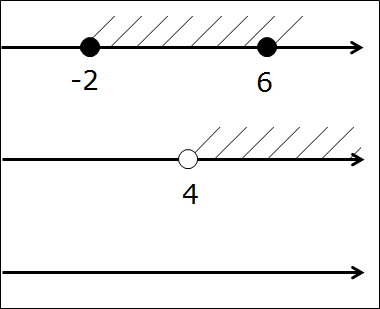
Вот так. Следующим шагом подштриховываем оба промежутка на одной оси. Чтобы не запутаться, для отличия пользуемся штриховкой с разных сторон оси в разных направлениях. Не нужно ювелирно штриховать по линеечке, мы не на черчении. Штрихуем грубо, брутально, но — разборчиво. Где-то штриховки будут встречаться одна под другой, образуя «ёлочку», но ничего не смущаемся, это — именно то, что нам и нужно! Получим такую картинку:
А теперь смотрим и соображаем: какой кусочек числовой оси подштрихован обоими видами штриховки одновременно? Верно! Кусочек между точками 4 и 6. Или — промежуток [4; 6]. Этот промежуток и будет пересечением промежутков [-2; 6] и [4; +∞). И все дела.)
Математически результат пересечения оформляют вот так:
[-2; 6] ⋂ [4; +∞) = [4; 6]
Значок «⋂» означает «пересечение».
Разбираем следующий пример. Пример совсем безобидный, но ступор у некоторых случается, да…)
Пересечём, например, промежутки:
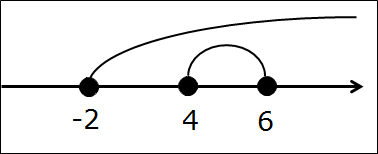
Рисуем. В этот раз я буду использовать второй способ рисования — дужки. Получим такую картинку:
И опять соображаем: какой кусок оси содержит точки обоих промежутков одновременно?
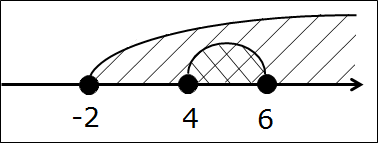
Не догадались? Тогда снова штрихуем промежутки в разных направлениях, прямо под дужками. И смотрим, где штриховки накладываются:
Ну и как, осенило? Да! Второй промежуток [4; 6] — и есть наше пересечение (т.е. общая часть)! Да, весь целиком. Дело всё в том, что второй промежуток, [4; 6], целиком содержится в первом [-2; +∞). Ничего страшного, так бывает.
В математической форме:
[-2; +∞) ⋂ [4; 6] = [4; 6]
Уловили идею? Ну-ка, быстренько закрепим успех!
Найдите пересечения следующих числовых промежутков:
Ответы (в беспорядке):
Что, примитив? Ну да, проще некуда. А вот сейчас начинаются первые сюрпризы! Я же обещал…)
Сюрприз первый — пустое множество
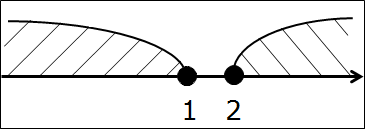
Попробуем пересечь, скажем, такие два промежутка:
(-∞; 1] ⋂ [2; +∞)
Дело нехитрое. Рисуем ось, точки-кружочки, помечаем дужками каждый промежуток, штрихуем, всё чин-чинарём…
И? Где здесь общая часть? А нигде! Нету такого кусочка оси, который был бы закрашен разными штриховками одновременно. На нет и суда нет. В таких случаях говорят, что данные промежутки не пересекаются.
Математически эта фишка записывается вот как:
(-∞; 1] ⋂ [2; +∞) = Ø
Этот перечёркнутый кружочек означает «пустое множество». Множество, в котором нет ни одного элемента. Ни одного числа… Очень частое явление. Особенно — при решении систем неравенств.
Сюрприз второй — изолированная точка
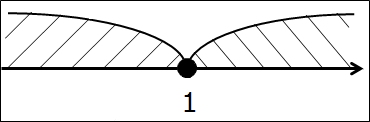
Всё то же самое, что и в предыдущем примере, только двойку во втором промежутке заменю на единичку. Вот так:
(-∞; 1] ⋂ [1; +∞)
Делать нечего, опять рисуем ось. В этот раз рисуем одну единственную точку 1. Закрашенную.
А здесь какие мысли насчёт пересечения? Да! Единственная общая часть — точка 1. Одна точка. Любая другая точка — правее ли единички, левее ли — попадает лишь в один из пересекаемых промежутков. Либо только в левый, либо только в правый. И только лишь единичка попадает в оба промежутка сразу.
В таких случаях результат пересечения (одна точка) оформляют так:
(-∞; 1] ⋂ [1; +∞) =
Фигурные скобочки в такой записи означают множество. Числовое множество. Единичка внутри фигурных скобок — элемент этого множества. Один-единственный. Или — изолированная точка.
Не следует думать, что пустое множество и изолированная точка –такая уж экзотика при решении неравенств. Такие сюрпризы попадаются в системах неравенств, в методе интервалов, в нахождении области определения функции, в уравнениях/неравенствах с модулем и прочих серьёзных темах. В соответствующих уроках убедимся.)
Кто читает вдумчиво, тот заметил, что слово «множество» я употребил в этом уроке уже не один раз. И это неспроста. Дело в том, что числовые промежутки и операции над ними — это знакомство с ещё одним новым разделом математики, помимо неравенств. Раздел называется «Теория множеств» и работает именно с множествами объектов самой разной природы. Числовыми промежутками, в том числе. Но множества — отдельная большая тема. Не в этот раз…
Полдела сделано. Можно заниматься наскальной живописью. Что-то типа такого:
Несведущий человек отшатнётся в ужасе. А сведущий сразу твёрдой рукой напишет:
(-∞; 1] ⋂ [0; 2] = [0; 1].
Так обычно оформляют пересечение промежутков в большинстве школ. Рисуют ось, штрихуют промежутки, ищут общую часть, да и записывают ответ. Такой способ хорош только в самых простых случаях. Пока точки — чёрные.
Проблемы начинаются с появлением выколотых точек.
Как работать с выколотыми точками?
Как только в игру вступают выколотые (т.е. незакрашенные) точки, вся простота куда-то испаряется напрочь… Особенно, если одна и та же точка в разные промежутки входит по-разному. Где-то она выколота, где-то закрашена… И в каком виде рисовать её на одной оси? Закрашивать её или нет?! Вот и путается народ…
Более того, обратите внимание! Во всех примерах этого урока мы пересекаем лишь два промежутка. Для простоты и понимания сути. А в более продвинутых заданиях (системы неравенств, нахождение ОДЗ и прочие крутые штучки) приходится пересекать и три, и пять… И все с разными кружочками и скобочками… Как не запутаться?
Есть, есть один секретный способ не запутаться! Но о нём — в конце урока.
А пока фиксируем в памяти одну простую вещь:
Операция пересечения — штука жёсткая. Если точка НЕ входит хотя бы в ОДИН из пересекаемых промежутков, то она автоматически НЕ входит и в окончательный результат пересечения.
Поясняю. Если какая-то точка хотя бы в одном из промежутков является выколотой, то нас уже не волнует, что там у неё с остальными промежутками (вторым, третьим, пятым…) — входит она в них или нет: в окончательный ответ такая точка УЖЕ не войдёт. Типа, даже если вы положили в борщ картошку, морковку, свёклу, лук, но в конце посолили стиральным порошком, кушать такой борщ вы уже не будете, да…) Уловили?
Разберём ценные зелёные слова на практике. Был у нас в самом начале урока примерчик:
[-2; 6] ⋂ [4; +∞)
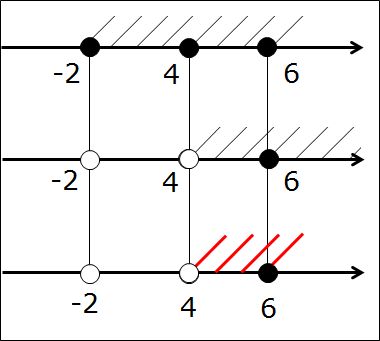
А теперь я немного видоизменю в нём один из промежутков. Сделаю во втором промежутке точку 4 выколотой. Т.е. скобочка перед четвёркой станет круглой. Вот такое пересечение теперь рассмотрим:
[-2; 6] ⋂ (4; +∞)
Рисуем, штрихуем, получаем картинку:
Ищем общую часть, записываем ответ:
[-2; 6] ⋂ (4; +∞) = (4; 6]
Кто в теме и врубился в слова «общая часть» и «одновременно», тот сразу всё понял. А кто не в теме, то… начинаем рассуждать. Примерно так:
А шестёрка? Тут без вопросов: в первый промежуток число 6 попадает на границу, но в закрашенном виде, а во второй (4; +∞) входит явно. Входит одновременно в оба? Да! Рисуем квадратную скобку: …6].
Итого: (4; 6].«
Вот так. Я же говорил, что ключевое слово здесь — одновременно!
Здесь-то ещё просто. А бывает куда злее! Когда неясно, как даже рисовать картинку-то… Например:
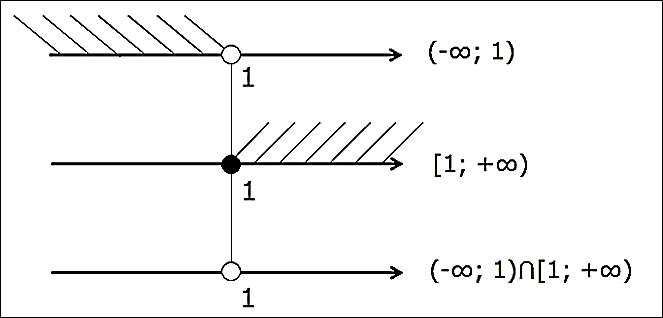
(-∞; 1) ⋂ [1; +∞)
Всё как обычно, рисуем прямую и отмечаем одну единственную граничную точку 1.
И… что-то не рисуется… В первом промежутке единичка с круглой скобкой, во втором — с квадратной. А ось — одна… Каким именно кружочком — пустым или закрашенным — рисовать единицу на оси? Непонятно…
Непонятно, если не понимать сути операции пересечения. А если понимать, то проблем — никаких. Наша граничная точка 1 в первый промежуток (-∞; 1) не входит. Выколота. Стало быть, при пересечении нам уже без разницы, закрашена ли единица во втором промежутке [1; +∞): в окончательный ответ она УЖЕ не войдёт!
Вывод: на оси точка 1 изображается выколотой. Т.е. незакрашенной.
Штриховки нигде не накладываются, а единственная разделяющая точка 1 — выколота. Ответ очевиден — пустое множество:
(-∞; 1) ⋂ [1; +∞) = Ø
Обычно именно так и поступают со всеми подозрительными точками. Берут конкретную точку, поочерёдно подставляют её в каждый из промежутков, анализируют, входит/не входит, и если хоть куда-то не входит — вычёркивают отовсюду. Так рисуются все белые точки. Потом собирают все точки, которые входят одновременно во все промежутки. И рисуют чёрными… И только потом рисуют окончательную картинку… Кошмар? Согласен, кошмар. Когда ось только одна, а точек разной раскраски — много.
Поэтому сейчас мы отдохнём от писанины и тягостных раздумий. А вместо этого — порисуем. Рисовать будем много, но зато результат окупится с лихвой. А количество ошибок резко сократится.)
Обещанный секретный способ!
Пересекаем промежутки без ошибок! Метод параллельных осей.
Итак, снова пересекаем те же самые промежутки: [-2; 6] ⋂ (4; +∞).
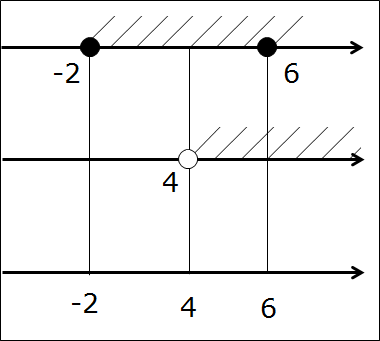
Сейчас берём в руки карандаш и рисуем… три параллельные оси! Всё правильно, именно три, я не обсчитался. На первых двух осях отдельно рисуем и штрихуем те промежутки, которые будем пересекать. Т.е. [-2; 6] и (4; +∞). На каждой из осей — свой. Соблюдаем одинаковый масштаб по всем трём осям! Это важно. Зачем нужна третья ось? Сейчас узнаем.) Получим такую картинку:
Представили? Вот так:
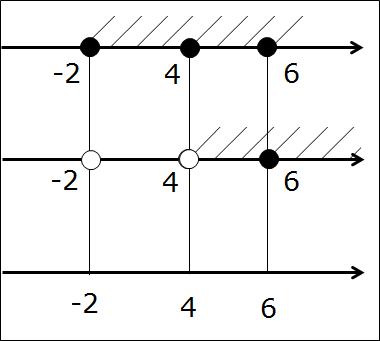
А нужны они нам — эти кружочки-то?! Ещё как! Самый ответственный, третий этап — рисуем нужные кружочки на третьей оси. Для этого рассуждаем так же, как и при прикидке в уме: если на первых двух осях обе точки чёрные, то и на третьей оси точка также чёрная. Если же хоть одна из двух точек выколота — на третьей оси точка также выколота!
Картинка станет вот такой:
Остались пустяки. Четвёртым этапом штрихуем на третьей прямой тот её кусочек, который заштрихован на первых двух прямых одновременно. Вот так:
Ответ: (4; 6]
Решаем тот самый злой пример с единичкой и пустым множеством: (-∞; 1) ⋂ [1; +∞)
Рисуем картинку с тремя осями и сразу видим всю необходимую информацию:
Безо всяких сомнений ясно, что единичка — выколота, а штриховать на третьей оси и вовсе нечего…
Ответ: Ø
Переходим к следующей важной операции — к объединению промежутков. В следующем уроке…
Равенство и неравенство. Знаки: больше, меньше, равно
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
Ø (латиница)
Ø (латиница)
Это — статья о букве расширенной латиницы Ø. Не следует путать её с ∅ (знаком пустого множества) и с ⌀ (символом диаметра)
| Буква латиницы Ø | ||||||
|---|---|---|---|---|---|---|
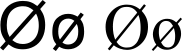 | ||||||
| Латинский алфавит | ||||||
| A | B | C | D | E | F | G |
| H | I | J | K | L | M | N |
| O | P | Q | R | S | T | U |
| V | W | X | Y | Z | ||
| Дополнительные и вариантные знаки | ||||||
| À | Á | Â | Ã | Ä | Å | Æ |
| Ā | Ă | Ą | Ç | Ć | Ĉ | Ċ |
| Č | Ð,ð | Ď,ď | Đ,đ | È | É | Ê |
| Ë | Ē | Ė | Ę | Ě | Ə | Ĝ |
| Ğ | Ġ | Ģ | Ĥ | Ħ | Ì | Í |
| Î | Ï | Ī | Į | İ,i | I,ı | IJ |
| Ĵ | Ķ | Ļ | Ł | Ñ | Ń | Ņ |
| Ň | Ò | Ó | Ô | Õ | Ö | Ø |
| Ő | Œ | Ơ | Ŕ | Ř | ß | ſ |
| Ś | Ŝ | Ş | Š | Þ | Ţ | Ť |
| Ù | Ú | Û | Ü | Ū | Ŭ | Ů |
| Ű | Ų | Ư | Ŵ | Ý | Ŷ | Ÿ |
| Ź | Ż | Ž | ||||
Ø и ø (латинская O диагонально перечёркнутая) — заглавная и строчная буквы, соответственно, используемые в датском, норвежском и фарерском алфавитах. Модификация латинской буквы O.
| ASCII | Юникод | HTML-мнемоника | |
| Ø (заглавная) | D8h | 00D8h | Ø |
| ø (строчная) | F8h | 00F8h | ø |
См. также
Полезное
Смотреть что такое «Ø (латиница)» в других словарях:
Đ (латиница) — Буква латиницы Đ, đ (дьже) Латинский алфавит A B C … Википедия
Ð (латиница) — Буква латиницы Ð, ð (eth) Латинский алфавит A B C … Википедия
латиница — алфавит, письмо, латинский алфавит Словарь русских синонимов. латиница см. латинский алфавит Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Алексан … Словарь синонимов
Латиница — наряду с кириллицей (см.) и глаголицей (см.) одна из славянских азбук, представляющая применение букв латинского алфавита для начертания славянских звуков. Первые попытки такого применения известны еще до кириллицы и глаголицы, но эти попытки… … Литературная энциклопедия
ЛАТИНИЦА — см. Латинское письмо … Большой Энциклопедический словарь
ЛАТИНИЦА — ЛАТИНИЦА, латиницы, муж. (филол.). Латинский алфавит, латинское письмо. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЛАТИНИЦА — ЛАТИНИЦА, ы, жен. Латинский алфавит. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Ł (латиница) — Польская буква Ł Латинский алфавит A … Википедия
Æ (латиница) — Лигатура Æ Латинский алфавит A … Википедия
IJ (латиница) — Нидерландская буква IJ Латинский алфавит A … Википедия
Œ (латиница) — Латинский алфавит A B C D E F G H I J K … Википедия
ЕСЛИ КРУГ ПЕРЕЧЕРКНУТ КРЕСТОМ — ЗНАЧИТ, В ДОМЕ ЕСТЬ МЕРТВЫЕ…
В тех случаях, когда требуется указать размер диаметра, используют знак в виде окружности с линией «Ø». Этот символ наносят перед размерным числом.
Примеры использования знака диаметра:
Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой «D» или знаком «Ø». Если радиус окружности умножить на два, суммой будет диаметр. Все объемные тела, имеющие сферическую форму, а также те, хотя бы одно из возможных сечений которых представляет собой круг, обозначаются символами диаметра. Слово «диаметр» произошло от греческого слова «diametros» – поперечник.
На технических чертежах диаметры обозначаются символом в виде перечеркнутой окружности «Ø». Данный знак, ставится перед размерными числами деталей, которые могут быть как цилиндрическими, так и коническими.
В сечение конус представляет собой прямоугольный треугольник, один из катетов которого параллелен или сосен телу вращения. Его параметры имеют следующими обозначениями: «D
» – больший диаметр, «d» – меньший диаметр, «L» – длина. На чертеже диаметры конуса обозначаются цифрами, перед которыми ставятся знаки «Ø» а числовое значение длинны без буквенных обозначений.
К наиболее распространенным деталям с цилиндрическими поверхностями, относятся валы различного назначения. Цилиндрические тела, образованные вращением прямоугольника около одной из его сторон обозначаются диаметром. Гладкие валы имеют некоторые конструктивные особенности, и разделяются на разновидности: прямые, ступенчатые односторонние, ступенчатые двусторонние и тяжелые. К примеру, валы асинхронных двигателей, в которых ротор сопрягается с валом методом запрессовки на наибольший его диаметр, а по обеим сторонам имеются ступени под подшипники, вентиляторы, и шкивы. Двусторонние ступенчатые валы можно встретить так же в различных механизмах там, где требуются, какие либо другие конструктивные особенности. Цилиндрические детали, как правило, имеют общую максимальную длину и наружный диаметр. В зависимости от конкретной конфигурации того или иного изделия в её состав могут входить такие элементы как внутренние и наружные канавки, ступени, выточки и др. с различными диаметрами перед значениями которых ставятся знаки «Ø
К деталям с коническими поверхностями относятся инструментальные переходные втулки, у которых наружная и внутренняя поверхность конические. Такие втулки обеспечивают высокую точность центрирования и быстродействие смены инструмента с достаточной жёсткостью при использовании их на станках. Переходные втулки бывают короткие и длинные.
Конические инструментальные детали данного типа называются «конус Морзе» и делятся на номера. Углы, длины и диаметры переходных втулок можно взять из специальных таблиц. В табличных данных используются буквенные обозначения такие как – «d» меньший диаметр, «D» большой диаметр, «L» длина детали. На чертежах диаметры и длины обозначаются цифровыми значениями, причём перед числами диаметра ставится знак «Ø».
«Конус Морзе» – помимо переходных втулок применяется при изготовлении хвостовиков спиральных свёрл, концевых фрез, приспособлений и оправок. Инструментальные конусы фиксируются за счёт упругой и пластической деформации. Для реализации таких соединений в шпинделях фрезерных и токарных станков, предусмотрены конические отверстия для установки вспомогательного инструмента. Кроме того у токарного станка пиноль задней бабки имеет такое же коническое отверстие.
В технике используются большое количество деталей и их элементов для обозначения, которых используется знак диаметра. Для стандартных размеров диаметров используются параметрический ряд, в который входят стандартные размеры. При разработке технических изделий расчётные диаметры округляются до ближайших их величин. При обозначении на технических чертежах знак диаметра должен сопровождаться обозначением оси штрихпунктирной линией, что указывает на круглое сечение участка детали.
В тулбаре своего смартфона пользователь может встретить массу всевозможных иконок, многие о котором ему совершенно ни о чем не говорят. Вот вы знаете, что означает перечеркнутый круг? Раз вы находитесь на этой странице, наверняка ваш ответ «нет».
Надо отметить, что это зависит от модели смартфона. В некоторых случаях перечеркнутый круг говорит о том, что в данный момент времени звук на смартфоне полностью выключен, то есть включен бесшумный режим. На других же — включен режим «Не беспокоить». Вот:
В этом примере показан включенный режим «Не беспокоить». Отключить его можно через панель быстрого доступа:
Просто нажмите на указанную иконку.
Режим «Не беспокоить» позволяет отключить определенные уведомления, но помните, что можно пропустить важный звонок или сообщение.
В свою очередь, в режиме «Не беспокоить» имеется выбор дополнительных режимов. В нашем примере это: «Полная тишина», «Только будильник», «Только важные».
Каким из них пользоваться, зависит от вашей потребности. Кстати, в других режимах «Не беспокоить» иконка может быть иной, вот пример:
Сделано это для удобства пользователя.
Что запрещает зачёркнутый крестом круг на ярлыке вашего джемпера?
Правда, сейчас зачастую вместо знаковых обозначений на ярлыках одежды пишут прямо словами, как нужно обращаться с вещью.
Правильный ответ: ХИМЧИСТКУ.
Если на ярлычке вашего джемпера вы увидели перечеркнутый круг, знайте, что вашему джемперу противопоказана химчистка.
Выбираем ответ — ХИМЧИСТКУ.
Перечеркнутый круг в данном случае запрещает химическую чистку этой вещи.
Верный ответ — ХИМЧИСТКУ.
Зачеркнутый круг на джемпере обозначает, что с ним нельзя quot;химичитьquot;.
Выбираем второй вариант ответа — химчистку.
Правильный ответ — ХИМЧИСТКУ.
Покупка одежды, особенно для женщин, дело любимое и увлекательное.
рой, окунувшись в шоппинг, милые дамы забывают обо всем на свете: мужчинах, доме, подругах и всех проблемах. Вернувшись, нам всем так хочется сразу одеть новую вещь и покрасоваться в ней при выходе. Проблемы начинаются тогда, когда дело доходит до ухода за одеждой. Часто бывает, что постирав кофточку или пиджачок, вещь садится и превращается в миниатюрную. Или же одежда начинает линять и красит все, что лежало рядом. Еще хуже — погладив любимую блузку, Вы с ужасом понимаете, что одно прикосновение раскаленным утюгом сделает дыры и пропалит изделие. Или вот вариант — посушив, как обычно, одежду на балконе или же в барабане, она превращается в бесцветное полотно. Что же следует делать, чтобы вещи служили Вам долго и преданно? Каких ошибок нельзя допускать при уходе за ними и как нужно стирать, сушить и гладить их? На эти вопросы ответы дадут значки и символы на этикетках, которых мы часто не замечаем.
Маркировка и информация о правилах эксплуатации, а также способах ухода за одеждой очень важны при уходе за любимыми изделиями. Об этом подробно могут рассказать значки и символы на этикетках вещей. Порой незаметные и маленькие, они играют очень важную роль в уходе за одеждой. Мы решили разобраться в них подробнее.
Первым и самым важным режимом, при уходе за текстильными изделиями, всегда была и есть стирка
. Значок с цифрой 60 означает, что стирка допускается при температуре, которая не превышает 60°C. Верхняя черта говорит про щадящий режим стирки.
Если Вы увидите значок с нарисованной рукой, он будет означать, что допускается лишь ручная стирка такой одежды.
Если же значок будет перечеркнут, стирка одежды вообще запрещена.
Отдельную группу составляют знаки, говорящие про правильное отбеливание
вещей. Треугольник означает, что изделия можно отбеливать любыми отбеливателями и средствами. Треугольник с полосками — разрешено отбеливание лишь кислородными средствами, которые на английском языке звучат как oxigen bleach. Треугольник с двумя большими буквами СL говорит о том, что допускаются только хлористые отбеливатели. Белый или черный перечеркнутые треугольники означают, что отбеливать такую одежду категорически запрещено. Знаки, которые регламентируют режим
глажки
скажут о таком. Утюг с тремя точечками на корпусе означает, что одежду можно гладить утюгом при максимальном нагреве.
Две точки на утюге говорят, что допускается лишь средний нагрев. Одна точка означает глажку при минимальном нагреве. И наконец, перечеркнутый утюг — глажка запрещается вообще. Режим химчистки
— еще один способ ухода за одеждой. Буква А в кружочке означает, что сухая химчистка допускается. В данном случае, А означает любой растворитель от английского слова «any». Буква Р в кружочке допускает обычную сухую химчистку с использованием углеводорода, хлорного этилена, монофлотрихлорметана. Очистители на основе растворителей с незначительными ограничениями разрешаются. Буква Р означает perchloroethylene. Буква Р в подчеркнутом круге говорит о том, что разрешается щадящая сухая химчистка с использованием углеводорода, хлорного этилена, монофлотрихлорметана. Буква F означает сухую химчистку с использованием углеводорода и трифлотрихлорметана. При этом категорически запрещено пользоваться очистителями на основе растворителей. Буква F переводиться как flammable, что пошло от «горючего». Буква F в подчеркнутом кружочке — щадящая сухая химчистка с использованием углеводорода и трифлотрихлорметана. При этом категорически запрещено пользоваться очистителями на основе растворителей. Перечеркнутый круг — химчистка запрещена. Английская буква W в кружочке допускает обычную влажную химчистку без ограничений. Буква W в кружке, подчеркнутом одной линией говорит о деликатной влажной химчистке со сниженным механическим воздействием. Буква W в кружке, который подчеркнут одной большой и одной маленькой линиями — деликатная влажная химчистка особо деликатных тканей со значительно сниженным механическим воздействием. Черный перечеркнутый кружок означает, что влажная химчистка категорически запрещена. Что касается
режима сушки
, кружок в квадрате означает, что сушка в барабанном устройстве разрешена. Кружок с двумя точками, обрамленный в квадрат допускает нормальную сушку. Одна точка в кружке, вокруг которого нарисован квадрат, говорит о том, что можно использовать режим только щадящей сушки. Наконец перечеркнутый кружок запрещает сушку в барабанном устройстве.
Стирка
Стирка — эта группа знаков, которая обозначает все манипуляции по стирке одежды, начиная от разрешения на стирку, заканчивая температурой и режимом. Главный символ в этой группе — таз с водой.
Добавляем знак диаметра в Microsoft Word
В текстовом редакторе MS Word есть довольно большой набор специальных символов, о котором, к сожалению, знают далеко не все пользователи этой программы. Именно поэтому, когда возникает необходимость добавить тот или иной символ, знак или обозначение, многие из них не знают, как это сделать. Одним из таких символов является обозначение диаметра, которого, как вы знаете, нет на клавиатуре.
Урок: Как добавить градусы Цельсия в Ворде
Добавление знака “диаметр” с помощью специальных символов
Все специальные символы в Word находятся во вкладке “Вставка”, в группе “Символы”, к которой нам и необходимо обратиться за помощью.
1. Установите курсор в том месте текста, где нужно добавить значок диаметра.
2. Перейдите во вкладку “Вставка” и нажмите там в группе “Символы” на кнопку “Символ”.
3. В небольшом окошке, которое развернется после нажатия, выберите последний пункт — “Другие символы”.
4. Перед вами откроется окно “Символ”, в котором нам и предстоит найти обозначение диаметра.
5. В разделе “Набор” выберите пункт “Дополненная латиница-1”.
6. Кликните по значку диаметра и нажмите кнопку “Вставить”.
7. Выбранный вами специальный символ появится в документе в указанном вами месте.
Урок: Как поставить галочку в Ворде
Добавление знака “диаметр” с помощью специального кода
Все символы, которые находятся в разделе “Специальные символы” программы Microsoft Word имеют свое кодовое обозначение. Если вы знаете этот код, вы можете добавлять необходимый символ в текст значительно быстрее. Увидеть этот код можно в окне символ, в его нижней части, предварительно кликнув по символу, который вам необходим.
Итак, чтобы добавить знак “диаметр” с помощью кода, выполните следующее:
1. Установите курсор в том месте, где необходимо добавить символ.
2. Введите в английской раскладке комбинацию “00D8” без кавычек.
3. Не перемещая указатель курсора с установленного места, нажмите клавиши “Alt+X”.
4. Знак диаметра будет добавлен.
Урок: Как поставить кавычки в Word
На этом все, теперь вы знаете, как вставить значок диаметра в Ворд. Используя набор специальных символов, доступных в программе, вы также можете добавлять в текст и другие необходимые знаки. Желаем вам успехов в дальнейшем изучении этой продвинутой программы для работы с документами.
Мы рады, что смогли помочь Вам в решении проблемы. Добавьте сайт Lumpics.ru в закладки и мы еще пригодимся вам. Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Отбеливание или выведение пятен
Эта группа обозначений на одежде показывает, какой тип отбеливателя можно применять к ткани, если такое возможно. Символ отбеливания — треугольник с надписями и без внутри.
Химическая чистка
Эта группа обозначений будет наиболее информативной для сотрудников службы химчистки, так как они означают типы химического воздействия на ткань. Символ значков химчистки — круг и различные буквы внутри него.
Значение татуировки круг
Самыми распространенными татуировками, имеющими форму круга, являются:
Инь и Ян
С древних времен символизирует единение двух начал – мужского и женского. Две разные по природе энергии взаимодействуют, обеспечивая носителю такого оберега защиту от злого влияния, приносят равновесие и успех в разных сферах жизни.

Татуировка круг — инь янь
Знак «Ом»
Берет начало в индуизме. Тату с ним имеет большое значение: помогает человеку всегда находить правильной решение в сложных ситуациях, легче переносить лишения и утраты. Он направляет мысли в нужное русло. Главное – нанести рисунок на верхнюю часть тела.

ТатТатуировка знака ОМ в круге
Круг, дополненный крестом
Является отсылкой к символу, популярному в религии древних египтян – Анкху. Он обозначает бессмертие, защиту от смертельной угрозы, способствует развитию отношений с противоположным полом.
Татуировка круг с крестом
Круг с точкой в центре
Такая татуировка имеет несколько значений.
Во-первых, она может символизировать колесо, как знак непрерывного движения вперед.
Во-вторых, так изображают часы, намекая на то, что жизнь постоянно возрождается, стрелки возвращаются в исходную точку и опять начинают движение.
В-третьих, окружность с обозначенной серединой ассоциируется с Солнцем, которым так любят украшать свое тело представители сильного пола. Данное небесное светило благоприятно воздействует на мужскую энергетику, придает сил, повышает потенцию.

Татуировка круг с токой в центре
Рисунок в виде спутницы Земли популярен у женщин. Луна является сильным оберегом, символизируя материнскую любовь, тепло, заботу, мудрость.

Татуировка круг в виде луны
Сочетание Солнца и Луны в одном тату
Подобно знаку «Инь и Ян» — показывает единение судеб двух людей противоположного пола. Рисунок-талисман защищает счастливый брак от негативного влияния со стороны.

Татуировка круг в виде солнца и луны в одной тату
Кольцо
Такое изображение, нанесенное на любую часть тела, символизирует бесконечность и неразрывность. Тату в виде кольца делают в знак счастливого союза двух сердец, преданности, обещания сдержать клятву или сохранить секрет.

Татуировка круг в виде парной тату колец
Три концентрических окружности
Показывают неразрывную связь этапов жизни человека – прошлого, настоящего, будущего. Это также символ везения, чудесного исцеления или спасения их опасной для жизни ситуации.

Татуировка трех окружностей
Переплетенные между собой круги
Знак единения жизни, непрерывного динамического движения.

Татуировка переплетенных кругов в треугольнике
Круг с крыльями
Является символом Солнца, его энергии, приносящей жизнь, плодородия.

Эскизы татуировки кругов с крыльями
Круг, переплетающийся с треугольником
Сложный рисунок, обозначающий единство человека и вселенной. Он также помогает изгнать злые помыслы из обладателя тату.

Татуировка круг переплетенный с треугольником
Круг, соединенный с квадратом
Изображение показывает неразрывную связь души и тела.

Татуировка круг с квадратом
Отжим
Эта группа значков описывает особенности отжима одежды во время стирки. Символ отжима — круг, вписанный в квадрат.
Сферические треугольники — использование в трехмерной графике
За последние несколько лет трехмерная компьютерная графика сделала гигантский шаг вперед. Качество и реалистичность, казавшиеся невозможными раньше, сейчас реализуются графическими ускорителями, доступными самому широкому кругу пользователей. Однако, принципы создания и визуализации трехмерных сцен и объектов практически не изменились. Базовым графическим примитивом по прежнему является треугольник. Каждый объект сцены разбивается на треугольники и в таком виде хранится и выводится на экран. Недостатки такого подхода очевидны: сложные объекты получаются либо слишком угловатыми, либо содержат огромное количество мелких треугольников, что приводит к существенному падению производительности. Таким образом, разработчикам и дизайнерам компьютерных игр приходится постоянно делать выбор между скоростью и качеством. Надо сказать, что разработано множество способов, позволяющих улучшить качество при минимальных вычислительных затратах, но даже они не способны скрыть угловатую сущность треугольника.
Почему бы тогда не отказаться от плоского треугольника в пользу более криволинейных геометрических примитивов? Дело в том, что использование кривых поверхностей в общем случае приводит к необходимости производить большое количество операций с вещественными числами. Такие примитивы используются в профессиональной трехмерной графике, но в системах визуализации в реальном времени (компьютерных играх) они не применимы в силу своей вычислительной сложности. Хотя и в этом направление ведутся работы, например в этой статье предлагается в качестве примитивов использовать квадрики с функциями возмущения, что позволяет создавать сложные формы объектов, используя минимум примитивов. Тем не менее, мне кажется, что в ближайшее время не стоит ожидать появления широко доступных графических ускорителей, способных обеспечить достаточно высокую скорость отрисовки подобных поверхностей.
В качестве альтернативы плоским треугольникам и сложным криволинейным функциям, я предлагаю рассмотреть такие графические примитивы, как сферические треугольники.
Сферический треугольник — это три точки на сфере, соединенные дугами большого круга. Наиболее интересны эйлеровы сферические треугольники — это те, что полностью лежат в одном полушарии. С одной стороны, они уже не являются плоскими объектами, а с другой — могут быть легко заданы тремя вершинами и радиусом окружности, на которой они лежат (радиусом кривизны). На самом деле это задание не однозначно — треугольник может быть как выпуклым, так и вогнутым. Будем считать, что треугольник с положительным радиусом кривизны — выпуклый, с отрицательным — вогнутый.
Использование сферических треугольников вместе с плоскими треугольниками дает множество преимуществ:
Иллюстрации к этой статье были отрендерены в специально написанной демонстрационной программе. Эта программа читает информацию о сцене из текстового файла, указанного в качестве параметра. Таким образом, можно создавать свои собственные сцены. Только нужно учесть, что эта программа не умеет выводить плоские треугольники — только сферические. Хотя сферический треугольник с большим радиусом кривизны вполне может сойти за плоский.
Проекция сферического треугольника на картинную плоскость с наложением текстуры
Будем считать, что нам известны следующие параметры сферического треугольника:
Прежде всего, нужно найти центр сферы, на которой лежит этот треугольник.
Для этого, рассмотрим плоскость, в которой лежат все три вершины A, B, C треугольника. Пересечение сферы и плоскости дает окружность, которая является описанной вокруг треугольника окружностью. Ее центр P лежит в точке пересечения срединных перпендикуляров и может быть найден по следующей формуле:
Если детерминант в знаменателе равен нулю, его можно заменить на такой же, но с другой парой координат — (y, z) или (x, z). Один из них будет неравен нулю хотя бы потому, что векторное произведение a и b ненулевой вектор.
Вектор с началом в центре сферы O и концом в центре окружности P коллинеарен вектору нормали n. Таким образом, мы получаем прямоугольный треугольник APO, гипотенуза и один катет которого известны. Это позволяет найти точку O по следующей формуле:
От знака перед корнем в этой формуле зависит будет треугольник выпуклым или вогнутым. Мы договорились, что выпуклость/вогнутость будет задаваться знаком радиуса, именно в этом месте он и играет роль.
Центр сферы достаточно найти только один раз — в дальнейшем, нужно лишь применять к нему те же трансформации, что и к вершинам.
Предположим, что геометрию мы рассчитали и теперь нужно вывести сферический треугольник на картинную плоскость. Прежде всего, полезно определить видим ли он вообще. Плоский треугольник считается видимым, если его нормаль направлена в сторону картинной плоскости. Со сферическими треугольниками все немного сложнее. Сферический треугольник видим, если хотя бы один из векторов OA, OB, OC направлен в сторону картинной плоскости.
После проверки на видимость, сферический треугольник нужно спроецировать на картинную плоскость. Будем считать, что она совпадает с плоскостью z = 0, а проектирующие прямые параллельны оси Oz.
Процесс проецирования организуем следующим образом — просканируем все пиксели окна вывода картинной плоскости и для каждого определим цвет, если он лежит внутри сферического треугольника. На самом деле, существуют методы, позволяющие обойтись без сканирования всего окна вывода, ограничиться только пикселями, лежащими внутри границ треугольника. Проблема тут в том, что границы — это эллиптические кривые. Упомянутая выше демонстрационная программа реализует один из этих методов, причем с довольно высокой скоростью. Но этот способ довольно сложен и относится скорее к методам программной оптимизации, поэтому я оставлю его за рамками этой статьи. Будем считать, что сканируется все окно вывода.
Получив координаты (x, y) пикселя, нужно найти z координату точки X на сфере, проецирующейся в этот пиксель. Это можно сделать пользуясь следующей формулой:
Если выражение под корнем меньше нуля, то в данный пиксель не проектируется ни одна точка сферы. Если равно нулю, то существует только одна такая точка. Если больше нуля, то таких точки две — на внешней поверхности сферы и на внутренней. Какую из них выбрать — это опять вопрос выпуклости/вогнутости, а как следствие, знака радиуса.
Знание z-координаты дает множество возможностей, например, можно воспользоваться z-буфером для проверки видимости.
Чтобы избавиться от этих эффектов, я предлагаю разлагать вектор AX по базису векторов AB, AC и OX. Использование вектора OX привносит нелинейные искажения, «растягивающие» текстуру на весь сферический треугольник. Разложение осуществляется следующими формулами (нам нужны только первые две координаты, поэтому третью формулу я опустил):
Текстурные координаты (Xu, Xv) находятся по следующим формулам:
Зная текстурные координаты и текстуру, найти цвет пикселя уже легко.
Хотя формулы выглядят довольно громоздко, их программная реализация работает достаточно быстро.
Некоторые проблемы и пути их решения
При моделировании «летающей тарелки» у меня возникла следующая проблема:
Оказалось, что как бы я ни старался, уголки треугольников торчат в месте стыка. Дело в том, что, как я уже писал, сферический треугольник образуется тремя дугами больших кругов. А это значит, что только в районе экватора нижние грани треугольников лежат в одной плоскости. Но тогда «тарелка» вырождается в сферу. Можно разбить каждую половинку на множество сферических треугольников, но это противоречит самой идее использования этих примитивов.
Чтобы избавиться от этих артефактов, я предлагаю следующий метод. Сферическому треугольнику дополнительно назначается плоскость (A, B, C, D), а также два числа Dmin и Dmax — начальное и конечное расстояние от плоскости, диапазон, по которому отсекается треугольник. То есть, в процесс проектирования добавляется проверка:
Эта проверка позволяет значительно расширить возможности сферических треугольников. Например, используя этот метод, можно получить такой объект:
При этом, падения скорости не наблюдается, временами даже наоборот.
Заключение
Использование сферических треугольников в задачах компьютерной графики имеет как свои плюсы, так и минусы. Очевидно, что эти примитивы не смогут полностью удовлетворить разработчиков трехмерных приложений или вытеснить плоские треугольники. Я ни в коем случае не позиционирую описанные методы как альтернативу существующим системам. Но использование сферических треугольников совместно с другими технологиями способно дать еще одну степень свободы создателям трехмерных миров. Этим, наверное, стоит воспользоваться.
За подготовку иллюстраций благодарность Кондрату Ермолину
Сушка
Это последняя группа обозначений, которые можно встретить на ярлыках одежды и вещей. От этих значков зависит способ сушки — от естественного до машинного. Знак сушки — квадрат.
Глажка одежды
Теперь у вас есть представление о всех знаках, которые можно встретить на одежде. Будьте внимательны, и прежде чем срезать ярлык и выбросить его в урну, ознакомьтесь с уходом за приобретенной одеждой.
Покупая новую одежду, мы редко всматриваемся на знаки на ее этикетки, нас больше всего волнует, какой это размер и идет ли она нам по фигуре. Есть, конечно, еще и те, кто ищет знак какого-либо определенного бренда или лейбла. А между тем знаки на одежде при правильной расшифровке могут многое нам рассказать о вещи и заставить задуматься, а стоит ли покупать данную вещь? Сможем ли мы за ней правильно ухаживать? Не будет ли приобретенная вещь, несмотря на всю свою красоту нам в тягость?
На все эти вопросы можно получить ответ, расшифровав знаки на одежде. Они могут нам поведать, как правильно стирать (какой режим, температура воды), выжимать (сколько оборотов в минуту), сушить, гладить вещь (при какой температуре), а также можно ли ее отдавать в химчистку. Кроме того бирка на одежде содержит в себе информацию о стране производителя, название фирмы, пошившей данную вещь и многое другое. Стоит ли удивляться, что зачастую на качественных и фирменных вещах бирка очень и очень длинная.
Итак, что же означают все эти треугольнички, квадратики, кружочки и прочие геометрические фигуры (прям страница из учебника по геометрии)? Сегодня мы расскажем вам, что означают все эти знаки на бирке одежды.
Самые распространенные знаки на одежде расшифровка
Знаки, касающиеся стирки
Тазик с водой обозначает, что допускается машинная стирка вещи, т.е. в стиральной машине. Правда и здесь есть свои нюансы, касающиеся допустимой температуры воды, количества оборотов барабана в минуту.
Тазик с тремя точками в центре – это стирка в стиральной машине при температуре в 50⁰С.
Если под тазиком с водой две горизонтальные линии, то этот знак показывает, что вещь требует особой аккуратности при стирке – т.е. режим деликатной стирки + ускоренная программа полоскания.
Если на ярлыке приобретенной вами вещи красуется перечеркнутый тазик с водой, то это значит, что ее нельзя стирать в домашних условиях, поэтому выход один – отдать в химчистку.
Тазик с рукой, конечно, означает, что вещь можно стирать только вручную, а не в стиральной машинке.
Знаки, касающиеся отбеливания
Простой треугольник, означает, что вещь можно отбеливать любым средством, в том числе и хлорсодержащими средствами (иногда в такой треугольник помещают химическое обозначение хлора – «Cl»).
Треугольник с двумя вертикальными линиями под наклоном означает, что вещь можно отбеливать, но только теми средствами, что не содержат хлор.
Перечеркнутый треугольник на бирке – это предупреждение того, что вещь нельзя отбеливать.
Знаки, касающиеся отжима одежды
Простой круг на бирке одежды означает, что вещь можно отжимать любым способом.
Перечеркнутый круг – вещь нельзя вообще отжимать.
Круг в квадрате с тремя точками посередине – это знак того, что одежду можно отжимать при высоких температурах.
Перечеркнутый круг в квадрате на бирке одежды показывает, что вещь нельзя отжимать в стиральной машинке или специальной сушилке.
Знаки, касающиеся сушки
Знак похожий на конверт – это указание того, что вещь надо сушить старым добрым проверенным способом – на веревке, металлической сушилке или вешалке. Главное, чтобы она была в вертикальном положении.
Квадрат с стремя вертикальными линиями внутри – вещь необходимо вывешивать сушить без всякого отжима. Такую бирку зачастую можно встретить на одежде в пайетках и т.п.
Квадрат с одной горизонтальной линией посередине поясняет, что вещь можно сушить лишь в разложенном, горизонтальном положении, но не вывешивать.
Квадрат с двумя диагональными линиями в углу предупреждает, что вещь можно сушить лишь в тени, но никак не под солнышком. Обычно такой знак моно увидеть на бирках ярких вещей, т.е. где может выгореть краска.
Перечеркнутый квадрат означает, что вещь нельзя сушить, а следовательно и стирать, т.е. такой знак сопровождает знак о запрете стирки – перечеркнутый таз с водой.
Перечеркнутая «конфетка», а точнее это скрученная одежда означает, что вещь нельзя отжимать.
Знаки, касающиеся глажки
Рисунок утюга значит, что вещь можно гладить
Знак на бирке утюг с одной точкой в центре – это разрешено гладить при самой низкой температуре. На утюгах это не более 90⁰С. Как правило такой знак можно встретить на изделиях из шелка, нейлона и прочих тонких и нежных тканях.
Знак на бирке утюг с двумя точками в центре — это разрешено гладить при средних температурах, т.е. около 150⁰С.
Знак на бирке утюг с тремя точками в центре — это разрешено гладить при высоких температурах, т.е. при 200⁰С.
Если на бирке нарисован утюг, а под ним перечеркнуты две вертикальные линии (символизируют пар), то это значит, что вещь можно гладить, но нельзя использовать отпаривание.
Перечеркнутый утюг – это запрет гладить вещь.
Детальное описание знаков на ярлыках
Ниже будет приведено детальное описание знаков, присутствующих на ярлычках, а также их полная расшифровка: