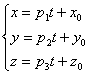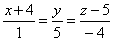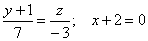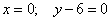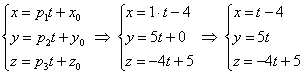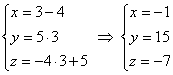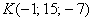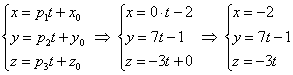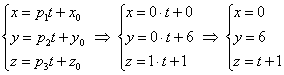Что значит параметрическое уравнение

Параметрическое уравнение прямой. Параметрическое уравнение прямой в пространстве

Прямая вместе с точкой являются важными элементами геометрии, с помощью которых строятся многие фигуры в пространстве и на плоскости. В данной статье подробно рассматривается параметрическое уравнение прямой, а также его связь с другими типами уравнений для этого геометрического элемента.

Прямая и уравнения для ее описания

Прямая в геометрии представляет собой совокупность точек, которые соединяют произвольные две точки пространства отрезком с наименьшей длиной. Этот отрезок является частью прямой. Любые другие кривые, соединяющие зафиксированные две точки в пространстве, будут иметь большую длину, поэтому прямыми не являются.

Вам будет интересно: Тайны «Аненербе»: история, артефакты, архивы

Существуют несколько видов уравнений прямой, с помощью которых можно описать прямую в трехмерном пространстве или в двумерном. Ниже приведены названия этих уравнений:

В данной статье рассмотрим параметрическое уравнение прямой, однако выведем его из векторного. Также покажем связь параметрического и симметричного или канонического уравнений.

Уравнение векторное

Понятно, что все приведенные типы уравнений для рассматриваемого геометрического элемента связаны между собой. Тем не менее векторное уравнение является базовым для всех них, поскольку оно непосредственно следует из определения прямой. Рассмотрим, как оно вводится в геометрию.

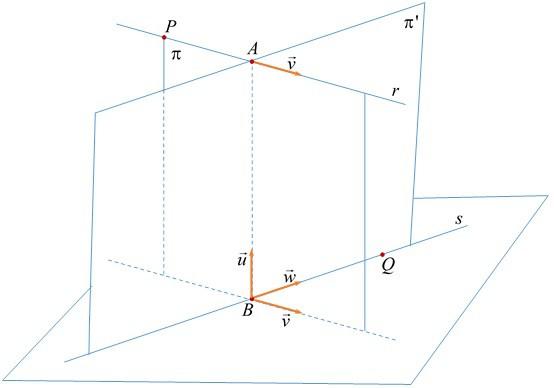
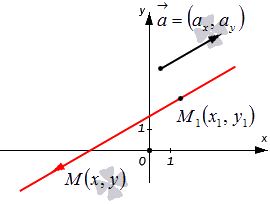
(x; y; z) = (x0; y0; z0) + α × (a; b; c)

Здесь символ α является параметром, принимающим абсолютно любое действительное значение (умножение вектора на число может изменить только его модуль или направление на противоположное). Это равенство называется векторным уравнением для прямой в трехмерном пространстве. Изменяя параметр α, мы получаем все точки (x; y; z), которые образуют эту прямую.

Вам будет интересно: А. Пушкин «Песнь о вещем Олеге»: жанр и идея

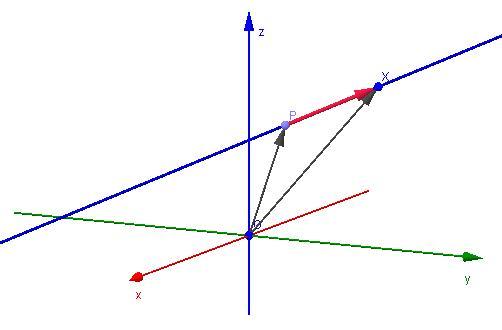
Стоящий в уравнении вектор v¯(a; b; c) называется направляющим. Прямая не имеет конкретного направления, а ее длина является бесконечной. Эти факты означают, что любой вектор, полученный из v¯ с помощью умножения на действительное число, также будет направляющим для прямой.

Что касается точки P(x0; y0; z0), то вместо нее в уравнение можно подставить произвольную точку, которая лежит на прямой, и последняя при этом не изменится.

Рисунок выше демонстрирует прямую (синяя линия), которая задана в пространстве через направляющий вектор (красный направленный отрезок).

Не представляет никакого труда получить подобное равенство для двумерного случая. Используя аналогичные рассуждения приходим к выражению:

(x; y) = (x0; y0) + α × (a; b)

Видим, что оно полностью такое же, как и предыдущее, только используются две координаты вместо трех для задания точек и векторов.

Уравнение параметрическое

Сначала получим в пространстве параметрическое уравнение прямой. Выше, когда записывалось векторное равенство, уже упоминалось о параметре, который в нем присутствует. Чтобы получить параметрическое уравнение, достаточно раскрыть векторное. Получаем:

Параметрическое уравнение прямой на плоскости подобно таковому для пространственного случая. Оно записывается в виде:

Таким образом, чтобы составить параметрическое уравнение прямой, следует записать в явном виде векторное уравнение для нее.

Получение уравнения канонического

Как выше было отмечено, все уравнения, задающие прямую в пространстве и на плоскости, получаются одно из другого. Покажем, как получить из параметрического уравнения прямой каноническое. Для пространственного случая имеем:

Выразим параметр в каждом равенстве:

Поскольку левые части являются одинаковыми, тогда правые части равенств тоже равны друг другу:

Это и есть каноническое уравнение для прямой в пространстве. Значение знаменателя в каждом выражении является соответствующей координатой направляющего вектора. Значения в числителе, которые вычитаются из каждой переменной, представляют собой координаты точки, принадлежащей этой прямой.

Соответствующее уравнение для случая на плоскости примет вид:

Дальше в статье решим несколько задач, используя полученные знания.

Уравнение прямой через 2 точки

Известно, что две фиксированные точки как на плоскости, так и в пространстве однозначно задают прямую. Предположим, что заданы две следующие точки на плоскости:

Как составить уравнение прямой через них? Для начала следует определить направляющий вектор. Его координаты имеют следующие значения:

Теперь можно записать уравнение в любом из трех видов, которые были рассмотрены в пунктах выше. Например, параметрическое уравнение прямой принимает вид:

В канонической форме можно переписать его так:

Видно, что в каноническое уравнение входят координаты обеих точек, причем в числителе можно менять эти точки. Так, последнее уравнение можно переписать следующим образом:

Все записанные выражения называются уравнениями прямой через 2 точки.

Задача с тремя точками

Даны координаты следующих трех точек:

Необходимо определить, лежат эти точки на одной прямой или нет.

Решать эту задачу следует так: сначала составить уравнение прямой для любых двух точек, а затем подставить в него координаты третьей и проверить, удовлетворяют ли они полученному равенству.

Составляем уравнение через M и N в параметрической форме. Для этого применим полученную в пункте выше формулу, которую обобщим на трехмерный случай. Имеем:

Теперь подставим в эти выражения координаты точки K и найдем значение параметра альфа, который им соответствует. Получаем:

Мы выяснили, что все три равенства будут справедливы, если каждое из них примет отличающееся от других значение параметра α. Последний факт противоречит условию параметрического уравнения прямой, в котором α должны быть равны для всех уравнений. Это означает, что точка K прямой MN не принадлежит, а значит, все три точки на одной прямой не лежат.

Задача на параллельность прямых

Даны два уравнения прямых в параметрическом виде. Они представлены ниже:

Необходимо определить, являются ли прямые параллельными. Проще всего определить параллельность двух прямых с использованием координат направляющих векторов. Обращаясь к общей формуле параметрического уравнения в двумерном пространстве, получаем, что направляющие вектора каждой прямой будут иметь координаты:

Два вектора являются параллельными, если один из них можно получить путем умножения другого на некоторое число. Разделим попарно координаты векторов, получим:

Направляющие вектора v2¯ и v1¯ параллельны, значит, прямые в условии задачи тоже являются параллельными.

Проверим, не являются ли они одной и той же прямой. Для этого нужно подставить координаты любой точки в уравнение для другой. Возьмем точку (-1; 3), подставим ее в уравнение для второй прямой:

То есть прямые являются разными.

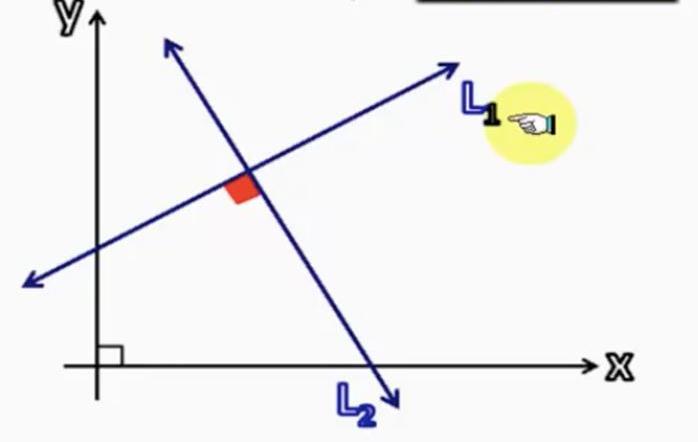
Задача на перпендикулярность прямых

Даны уравнения двух прямых:

Перпендикулярны ли эти прямые?

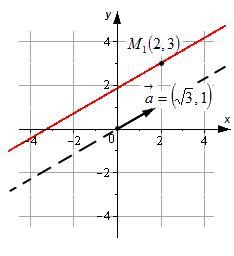
Две прямые будут перпендикулярны, если скалярное произведение их направляющих векторов равно нулю. Выпишем эти вектора:

Найдем их скалярное произведение:

Таким образом, мы выяснили, что рассмотренные прямые перпендикулярны. Они изображены на рисунке выше.

Источник

5.4.3. Параметрические уравнения прямой

Важнейший вид! Да, параметрические уравнения, конечно, не альфа и омега пространственной геометрии, но «рабочая лошадка» многих задач. Причём, этот вид уравнений часто применяется неожиданно, и я бы сказал, изящно.

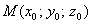
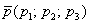
Если известна точка , принадлежащая прямой, и направляющий вектор данной прямой, то параметрические уравнения этой прямой задаются системой:

Всё проще пареной репы, поэтому придётся приперчить задачу:

Задача 149

Составить параметрические уравнения следующих прямых:

а)

б)

в)

Решение: прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

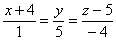
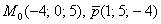
а) Из уравнений «снимаем» точку и направляющий вектор: . Точку можно выбрать и другую (как это сделать – рассказано после Задачи 143), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

Одно из удобств состоит в том, с помощью этих уравнений легко находить как раз другие точки прямой. Например, найдём точку , координаты которой, скажем, соответствуют значению параметра :

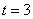
Таким образом:

Составим параметрические уравнения прямой:

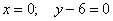
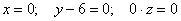
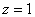
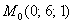
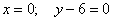
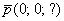
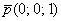
в) Перепишем уравнения в виде , то есть «зет» может быть любым. А если любым, то пусть, например, . Таким образом, точка принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях находятся «икс» и «игрек», и в направляющем векторе на этих местах записываем нули: . На оставшееся место ставим единицу: . Вместо единицы подойдёт любое число, кроме нуля, но единица лаконичнее всего.

Запишем параметрические уравнения прямой:

И в академичном стиле тут ещё можно записать ответ, в котором под пунктами «а», «бэ» и «вы» перечислить полученные уравнения.

Аналогичное задание для самостоятельного решения:

Задача 150

Составить параметрические уравнения следующих прямых:

а) ;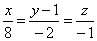

б) ;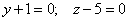

в) прямая проходит через точки .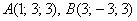

Решения в конце книги. Полученные вами ответы могут несколько отличаться от моих ответов, дело в том, что параметрические уравнения можно записать не единственным способом. Важно, чтобы ваши и мои направляющие векторы были коллинеарны, и ваша точка «подходила» к моим уравнениям (ну, или наоборот, моя точка – к вашим уравнениям :).

Как ещё можно задать прямую в пространстве? Хочется что-нибудь придумать с вектором нормали. Но тут ничего не получится – у пространственной прямой нормальные векторы могут смотреть совершенно в разные стороны.

Ещё один способ уже несколько раз «проскакивал» ранее:

Источник

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

Составление параметрических уравнений прямой на плоскости

Решение

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

Ответ: x = 2 + 3 · λ y = 3 + λ

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

При этом не должно смущать, если a x или a y будут равны нулю.

Решение

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

Решение

Для начала осуществим переход к каноническому уравнению:

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Разрешим полученные уравнения относительно переменных x и y :

x = x 1 + a x · λ y = y 1 + a y · λ

Решение

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

Решение

Решение

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

Решение

Решение

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

Источник

Параметрическое уравнение прямой на плоскости

В данной статье мы рассмотрим параметрическое уравнение прямой на плоскости. Приведем примеры построения параметрического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим методы преобразования уравнения в параметрическом виде в канонический и общий виды.

Параметрическое уравнение прямой L на плоскости представляется следующей формулой:

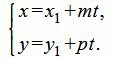(1)

Отметим что при записи уравнения прямой в параметрическом виде, направляющий вектор прямой не должен быть нулевым вектором, т.е хотя бы один координат направляющего вектора q должен быть отличным от нуля.

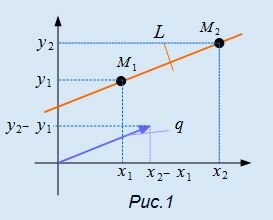
Для построения прямой на плоскости в декартовой прямоугольной системе координат, заданной параметрическим уравнением (1), достаточно задать параметру t две разные значения, вычислить x и y и провести через эти точки прямую линию. При t=0 имеем точку M₁(x₁, y₁) при t=1, получим точку M₂(x₁+m, y₁+p).

Для составления параметрического уравнения прямой на плоскости L достаточно иметь точку на прямой L и направляющий вектор прямой или две точки, принадлежащие прямой L. В первом случае, для построения параметрического уравнения прямой нужно координаты точки и направляющего вектора вставить в уравнение (1). Во втором случае сначала нужно найти направляющий вектор прямой q=<m, p>, вычисляя разности соответствующих координатов точек M₁ и M₂: m=x₂−x₁, p=y₂−y₁(Рис.1). Далее, аналогично первому случаю, подставить координаты одной из точек (не имеет значение какой именно) и направляющего вектора q прямой в (1).

Можно также вывести формулу параметрического уравнения прямой, проходящей через две точки. Для этого подставим значения m=x₂−x₁, p=y₂−y₁ в (1), получим параметрическое уравнение прямой на плоскости, проходящей через точки M₁(x₁, y₁) и M₂(x₂, y₂):

Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=<−3, 5>. Построить параметрическое уравнение прямой.

Решение. Для построения параметрического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

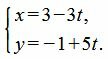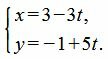Пример 2. Прямая проходит через точки M₁=(−5, 2) и M₂=(−2, 3). Построить параметрическое уравнение прямой.

Решение. Воспользуемся формулой (2). Подставим координаты точек M₁ и M₂ в уравнение (2):

Упростим полученное уравнение:

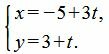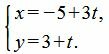Приведение параметрического уравнения на плоскости к каноническому виду

Выразим параметр t в (1) через переменные x и y:

Из выражений (3), можем записать каноническое уравнение прямой на плоскости:

Обратное преобразование смотрите здесь.

Пример 3. Прямая на плоскости представлена следующим параметрческим уравнением:

Привести данное уравнение прямой к каноническому виду.

Решение: Выразим параметр t через переменные x и y:

Из выражений (5), можем записать:

Приведение параметрического уравнения на плоскости к общему виду

Для приведения параметрического уравнения прямой на плоскости к общему виду, в формулах (1) выразим из второго уравнения параметр t через переменную y и подставим в первое уравнение:

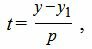Умножим обе части уравнения (6) на p и группируем элементы уравнения:

Сделаем обозначения: A=p, B=−m, C=−px₁+my₁. Тогда получим общее уравнение прямой:

Обратное преобразование смотрите здесь.

Пример 4. Прямая на плоскости представлена следующим параметрческим уравнением:

Привести данное уравнение прямой к общему виду.

Решение: В уравнении (9) имеем: x₁=−5, y₁=0, m=4, p=−2. Подставим эти значения в формулу (7):

Упростив выражение (10) получим общее уравнение прямой (9):

Источник

Краткое описание

В геометрии прямая линия представляет собой совокупность обычных точек, которые соединяют любые две точки пространства отрезком небольшой длины. Он является неотъемлемой частью прямой. Все кривые линии, которые будут пересекаться в зафиксированных двух точках, в итоге получат большую длину, из-за чего они не могут называться прямыми. Понять все тонкости поможет универсальная параметризация (моделирование и проектирование с использованием параметров элементов модели и соотношений между ними).

В геометрии принято различать несколько разновидностей уравнений параметрического типа. С их помощью можно лаконично и правильно описать окружность прямой в двухмерном или трёхмерном пространстве. Специалисты различают следующие разновидности уравнений:

Лучше всего начать изучение параметрического уравнения прямой в пространстве на векторном примере.

Этот метод чаще всего используют в школах при объяснении темы. Нелишним также будет узнать связь параметрического уравнения с симметричным. В каждом случае действуют свои правила, которые нельзя оставлять без внимания.

Ключевые особенности

Представление прямой К в уравнении имеет обычную формулировку: в=в1+nr/c=c1+wr. В этом случае в1 и с1 являются координатами точки M1 на прямой К. Вектор q= считается направляющим элементом отрезка К. Используемый символ r отображает некоторый параметр.

При записи уравнения направляющий вектор не должен быть нулевым. Для самостоятельного построения отрезка на поверхности в декартовой прямоугольной системе координат, которая была задана соответствующими уравнениями, достаточно задать параметру r две разные величины, правильно вычислить в и с, а также провести через эти две точки прямые параллельные линии.

Чтобы составить нормальное уравнение прямой линии на плоскости К, достаточно иметь точку на этой линии и направляющий вектор (можно заменить двумя точками). В первом случае нужно все координаты точки и направляющего вектора вставить в конструкцию. Во второй ситуации необходимо первым делом найти направляющий вектор для прямой q=. Обязательно нужно вычислить разность точек М1 и М2: в=в2-в1, w=с2-с1. После этого остаётся только правильно подставить координаты одной из точек и направляющего вектора (q).

При желании также можно вывести формулу параметрического уравнения, когда одна линия проходит сразу через две точки. Для этого нужно подставить значения m= в2-в1, w=с2-с1. За счёт этого можно получить уравнение отрезка на плоскости, которая проходит через точки М1 (в1, с1) и М2 (в2, с2). Решение таких задач считается элементарным, но важно не запутаться во всех формулировках.

Значение векторного типа

Все разновидности примеров в геометрии тесно связаны друг с другом. В качестве основы для них выступает векторное уравнение, так как именно оно следует из определённой прямой. Для примера можно рассмотреть ситуацию, когда в пространстве дана точка Y (t0, e0, x0). По условиям известно, что она принадлежит прямой. В этом случае можно провести бесконечное количество линий.

Для проведения единственной прямой следует правильно задать направление, которое определяется вектором. Для обозначения можно задействовать v (a, b, c). Символы в скобках являются координатами. Для всех точек W (s, z, m), которые расположены на конкретной прямой, можно написать логическое равенство: (s, z, m) = (t0, e0, x0) + а*v — (a, b, c).

В приведённом примере был взят символ а, который может принимать любое значение. Если попробовать умножить вектор на определённое число, то в итоге можно будет изменить не только первоначальный модуль, но и направление. Это равенство принято называть векторным уравнением для прямой в трёхмерном пространстве. Если правильно оперировать параметром а, то в итоге можно получить все точки (s, z, m), которые сформируют одну линию.

Если нужно определиться с точкой Y (t0, e0, x0), то в качестве примера вместо неё можно задействовать произвольную точку, которая лежит на прямой. Когда приведённый пример сопоставить с двухмерной реальностью, можно будет получить следующую формулу: (s, z) = (t0, e0) + а * (a; b). Результат практически идентичен с предыдущим случаем, но только в этой ситуации применяются две координаты вместо привычных трёх для указания всех векторов и точек.

Универсальное каноническое уравнение

Специалистами было доказано, что все уравнения, которые задают прямую на плоскости и в пространстве, являются зависимыми друг от друга. Способ получения канонического уравнения из параметрического лучше рассмотреть на конкретном примере. Для пространственного случая свойственны следующие данные:

Теперь можно выразить необходимый параметр в каждом равенстве: g=(l — l0) / a; g=(e — e 0) / b; g=(s — s0) / c. Так как все левые части равенства являются идентичными, то правые тоже будут равны друг другу. Пример: g=(l — l0) / а=(e — e0) / b=(s — s0) / c. Он является обычным каноническим уравнением для прямой в пространстве. В каждом выражении значение определённого знаменателя представляет собой соответствующую координату направляющего вектора.

Из любой переменной обязательно вычитаются необходимые значения в числителе. Благодаря полученному результату можно построить уравнение таким образом, чтобы получить ответ в виде проекции на координатные плоскости.

Наглядный пример

Параметрическое уравнение прямой на плоскости можно получить в том случае, когда в полном объёме раскрыть векторный пример. Если всё сделать правильно, то в итоге можно получить следующие данные:

В этом случае представлена определённая совокупность трёхлинейных равенств, в каждом из которых есть только одна переменная координата и параметр j. Последний принято называть параметрическим уравнением обычных прямых линий в пространстве. Ничего нового введено не было, поскольку просто был записан смысл соответствующего векторного выражения.

Правильное решение параметрических уравнений в онлайн-режиме пользуется большим спросом, но для лучшего понимания этого направления в геометрии следует искать правильный ответ не только при помощи калькулятора, но и самостоятельно. Если внимательно изучить теорию, то можно сделать вывод, что параметризация прямой на плоскости идентична пространственному случаю. А это означает, что для составления уравнения параметрической прямой линии нужно записать для неё в явном виде векторное уравнение.

Задача с параметрическими прямыми на плоскости

Именно этот пример является актуальным, так как он чаще всего используется по отношению к прямоугольной системе координат. В задачах первого типа заданы определённые координаты точек, которые иногда могут принадлежать прямой, подробно описанной геометрическими уравнениями.

Задачи второго типа рассчитаны на то, что абитуриент составит необходимое геометрическое уравнение линии на плоскости в прямоугольной математической системе координат. Для поиска верного решения необходимо выполнить элементарный переход одной математической конструкции в другую. А вот в задачах третьего типа необходимо плавно преобразовать параметрические уравнения заданной прямой в иные виды уравнений, которые её определяют. В качестве примера следует изучить задачу.

Дана прямая линия в системе координат прямоугольного типа, которую можно определить обычным уравнением х=1-3/4*ϰ / у=-1+ϰ. Цель задачи: отыскать верные координаты какого-либо вектора прямой. Решение основано на том, что для достижения желаемого результата необходимо осуществить перевод к общему уравнению:

Коэффициенты х позволяют получить все необходимые координаты вектора. Это значит, что вектор прямой х=1-¾*ϰ /у=-1+ϰ после проделанных манипуляций будет иметь координаты 1, ¾.

Использование трёх точек

Такие задачи отличаются повышенной сложностью, поскольку для их решения необходимо обладать необходимыми знаниями. Для лучшего усвоения этой темы следует изучить следующий пример. По условиям задачи были даны координаты трёх точек:

Нужно правильно определить, лежат ли все эти точки на одной прямой линии. Первым делом необходимо выполнить следующие действия: составить уравнение прямой сразу для двух любых точек, а только после этого подставить координаты третьей точки, чтобы проверить, соответствуют ли они полученному равенству. Лучше всего в параметрической форме составить уравнение через H и D. Для решения лучше задействовать обычную формулу, которую подгоняют под трёхмерный случай. В итоге можно получить:

После этого остаётся только поочерёдно подставить в эти выражения координаты точки W и отыскать значение параметра альфа, который максимально им соответствует. Решение:

Проанализировав результат, можно понять, что все три равенства будут верны, но только в том случае, если каждое из них получит отличающееся от других значение параметра а. Конечно, последний факт логически противоречит условию параметрического геометрического уравнения прямой, в котором значение а должно быть равно для всех примеров. Это означает, что W прямой HD не принадлежит, из-за чего все три точки никак не могут лежать на одной плоскости.

Источник