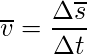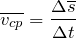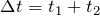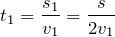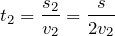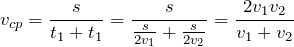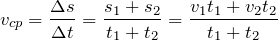Что значит отрицательная скорость на графике движения
Скорость движения
Скорость является одной из основных характеристик механического движения. Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.
Единицей измерения скорости в системе СИ является м/с.
Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по траектории движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).
К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.
Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).
Отрицательная скорость
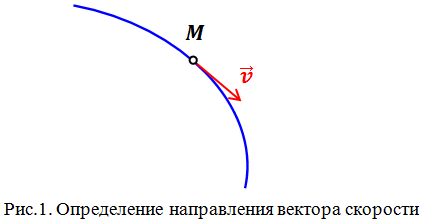
Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.
Равномерное и неравномерно движение
В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.
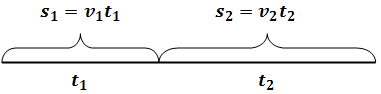
В случае неравномерного движения говорят о средней скорости:
Примеры решения задач по теме «Скорость»
| Задание | Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля. |
| Решение | Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей. |
Воспользуемся определением средней скорости:
Так как предполагается прямолинейное равномерное движение, знаки векторов можно опустить.
Время, потраченное автомобилем на прохождение всего отрезка пути:
где 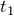
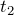
Суммарное перемещение равно расстоянию между населенными пунктами, т.е. 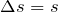
Подставив эти соотношения в формулу для средней скорости, получим:
Переведем скорости на отдельных участках в систему СИ:
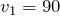
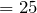
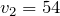
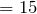
Тогда средняя скорость автомобиля:
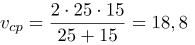
| Задание | Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 25 м/с. Определить среднюю скорость автомобиля. |
| Решение | Сделаем рисунок. |
Также как и в предыдущей задаче, знаки векторов в формуле опускаем. предполагая равномерное прямолинейное движение.
Время в системе СИ измеряется в секундах, переводим значение времени 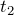
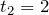
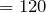
Средняя скорость автомобиля:
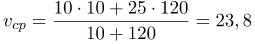
Может ли скорость быть отрицательной в физике?
В связи с этим, как считать минуты?
Чтобы преобразовать час в минуту, умножьте время на коэффициент преобразования. В время в минутах равно часам, умноженным на 60. Например, вот как преобразовать 5 часов в минуты, используя формулу выше.
Кроме того, что такое единица скорости?
Что означает T в скорости? vave = средняя скорость vi = начальная скорость vf = конечная скорость Другое определение средней скорости, которое работает при постоянном a. а = ∆v. ∆t. a = ускорение ∆v = изменение скорости ∆t = истекшее время время Определение ускорения.
Сколько 75 часов?
Таблица преобразования десятичных часов в минуты
| Минут | Десятые доли часа | Сотые доли часа |
|---|---|---|
| 43 | .7 | .72 |
| 44 | .7 | .74 |
| 45 | .7 | .75 |
| 46 | .7 | .76 |
Сколько минут в 2 часах?
Таблица перевода часов в минуты
| Часов | Минут |
|---|---|
| 1 час | 60 Минут |
| 2 часов | 120 Минут |
| 3 Часов | 180 Минут |
| 4 Часов | 240 Минут |
Как рассчитать 40 минут?
Скорость может быть отрицательной?
Скорость. … Так как конечное положение объекта (rfinal) может быть положительным, отрицательный, или ноль, а также больше, меньше или совпадает с начальным положением (rinitial), скорость может быть положительной, отрицательной или нулевой. Знак скорости зависит от системы координат, выбранной для определения положения.
Как скорость равна нулю?
Нулевая скорость по существу нет движения. Это означает, что ваше изменение положения время от времени a до момента b равно нулю. Это происходит, когда вы бросаете объект в небо. Непосредственно перед падением, когда нет силы, двигающей его вверх, он останется неподвижным и его скорость будет равна нулю.
Что такое единица силы в системе СИ?
Что такое текущая единица СИ?
Единица электрического тока: ампер (А)
Что означает vdt в физике?
Скорость, перемещение и время.
Чему равен C в физике?
Скорость света в вакууме, обычно обозначаемая c, является универсальной физической постоянной, важной во многих областях физики. Его точное значение определяется как 299792458 метров в секунду (примерно 300000 км / с или 186000 миль / с).
Что означает P в физике электричества?
Что такое 1/4 часа?
Какой процент составляет 20 минут в часе?
| Минут | Доля часа |
|---|---|
| 20 | 0.333 |
| 21 | 0.350 |
| 22 | 0.367 |
| 23 | 0.383 |
Что такое 6.75 часа в часах и минутах?
6.75 часов в часы и минуты
6.75 часа = 6 часов и минут 45.
Сколько часов составляет 1 час 30 минут?
1.5 часа следовательно, 1 час 30 минут.
Сколько минут в 2 днях?
Таблица перевода дней в минуты
| 1 день | 1440 |
|---|---|
| 2 дней | 2880 |
| 3 дней | 4320 |
| 4 дней | 5760 |
| 5 дней | 7200 |
Сколько секунд в 3 минутах?
Это то же самое, что сказать, что 3 минут является 180 секунды.
Что такое 50 часа?
Например, 30 минут равняется 50 процентам часа, а 10 минут равняются примерно 17 процентам часа.
Как написать 7 часов 30 минут?
7:30 читается как «семь часов 30 минут.
Скорость при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.
Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t0 и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:
v — скорость тела в данный момент времени, v 0 —скорость тела в начальный момент времени, a — ускорение тела, t — время, в течение которого это тело двигалось
Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.
Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.
Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.
Скалярная формула скорости
В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:
Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.
Проекция скорости
Проекция скорости при равноускоренном прямолинейном движении имеет вид:
Знак проекции скорости зависит от того, в какую сторону движется тело:
Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.
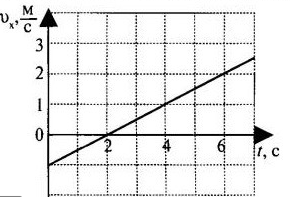
График скорости
График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является прямая.
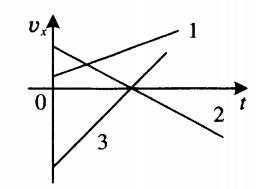
Сравнение модулей ускорения по графикам скоростей
Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.
Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.
На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.
Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.
Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:
Выразим начальную скорость:
Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Графики прямолинейного движения
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: \(\vec =0\).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: \(\vec =const\). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
Для каждого вида движения получим три графика. Графики будем называть так:
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой \(x_<0>\) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
\[x=x_<0>\]
Скорость и ускорение неподвижного тела равны нулю:
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка \(x_<0>\), а конечная координата — точка \(x\) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
Ускорение есть (рис. 4г) и оно не меняется:
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов \(\vec
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.