Что значит отрезки совпадают
Сравнение отрезков
Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:
Метод наложения:
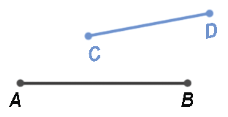
Пусть нам даны два отрезка AB и СD:
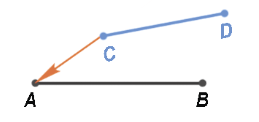
Совместим начало отрезка AB и СD (точки A и С).
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.
Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.
Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.
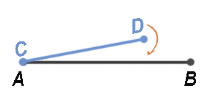
Рассмотрим еще одну пару отрезков HG и ST.
Совместим начало отрезка HG и ST.
Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.
В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.
Вывод:
Измерение длин:
Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.
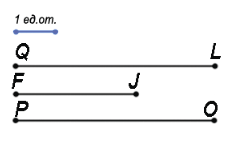
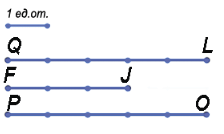
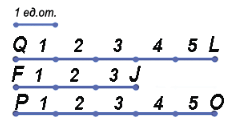
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.
Наложим единичный отрезок на данные.
Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.
Поделись с друзьями в социальных сетях:
Как сравнить два отрезка: способы и примеры
Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.
Способы сравнения двух отрезков
В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.
Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.
Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.
Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:
Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.
Измерение длины
Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.
Обратите внимание: что такое луч в геометрии.
Наложение друг на друга
Как происходит совмещение АБ и ВГ:
Сравнение в координатной сетке
Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1; Х2, Y2) и b (Х3, Y3; X4, Y4).
Первое, что нужно сделать — придать координатам числовые значения:
Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164
Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73
√ 164 > √ 73, значит, Da > Db.
Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.
Примеры
Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.
Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ 2, значит, CD>AB, то есть отрезок CD длиннее AB.
Сравнение отрезков. Действия над отрезками.
Равные и неравные отрезки
Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.
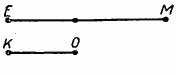
Сравним два отрезка КО и ЕМ (рис.). 
Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.
Записывается это тaк: ЕМ > КО, КО 1 /5 часть отрезка МN.
в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).
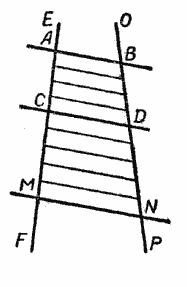
Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла
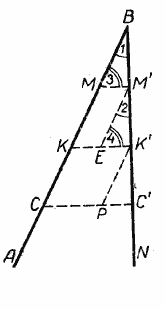
Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.
На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.
Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.
Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:
∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;
∠3 = ∠4, как острые углы 1 с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).
ВМ = МК по построению;
МК = М’Е, как противоположные стороны параллелограмма.
Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.
Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.
Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.
В этом случае вершину угла на чертеже можно не отмечать (рис.).
Теорема справедлива и для случая, когда прямые КО и МР параллельны.
Пропорциональные отрезки
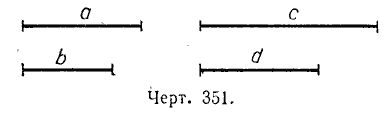
Из арифметики известно, что равенство двух отношений называется пропорцией. Например: 16 /4 = 20 /5; 2 /3 = 4 /6 To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.
отрезки а, b, c, d называются пропорциональными.
В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.
Поскольку в пропорции a /b = c /d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции a /x = c /d x = a • d /c
Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.
а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.
Чтобы убедиться в этом, переставим средние члены в этой пропорции.
А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.
В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.
Построение пропорциональных отрезков
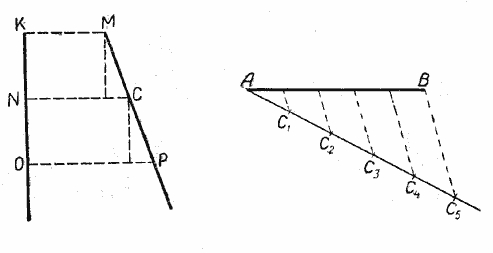
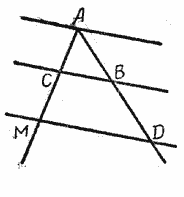
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).
Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.
Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.
Например, р = 4 см. и q = 5 см.
Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.
Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.
Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC /AM = BD /BN,
Теорема будет справедлива и при любых других целых значениях р и q.
Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.
Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.
Как сравнить два отрезка: способы и примеры
Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.
Способы сравнения двух отрезков
В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.
Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.
Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>,, <,, =). Например, длина отрезка АБ — 2 см, а ВГ — 8 см, записываем результат сравнения так: АБ <, ВГ или ВГ >, АБ.
Это интересно: как разложить на множители квадратный трехчлен?
Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:
Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.
Измерение длины
Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.
Обратите внимание: что такое луч в геометрии.
Наложение друг на друга
Как происходит совмещение АБ и ВГ:
Бывает так, что при наложении одного отрезка на другой ровно половина одного из них будет совмещена с другим. Точку, которая делит его на две равные части, называют серединной точкой. И если у нас есть серединная точка В, то АВ=ВБ.
Примерно так же наложением сравнивают не только прямые, но и другие геометрические фигуры, а также углы.
Можно сделать «линейку» из полоски бумаги, при этом такую линейку не нужно линовать, достаточно отметить на ней начало и конец одного из отрезков. Затем вы прикладываете импровизированную линейку ко второму, совмещая его начало с первой отметкой и, сравниваете расположение второй отметки по отношению к его концу. Таким способом можно сравнивать и довольно большие фигуры, например, расстояние между столбиками забора, но использовать при этом лучше не бумажную полоску, а веревку.
Два отрезка называются равными, если их можно совместить методом наложения. Если есть возможность приложить их друг к другу, просто посмотрите, какой из них длиннее. Но так можно сделать не всегда.
Если под рукой имеется циркуль, поставьте одну ножку циркуля в начало, а другую в конец первого отрезка. Затем не сдвигая ножки циркуля, установите одну из них в начало второго и посмотрите, если вторая ножка циркуля в точке, обозначающей конец — они равны. Если вторая ножка на самой прямой — первый отрезок меньше, если за ним — первый больше.
Сравнение в координатной сетке
Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1, Х2, Y2) и b (Х3, Y3, X4, Y4).
Первое, что нужно сделать — придать координатам числовые значения:
Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164
Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73
√ 164 >, √ 73, значит, Da >, Db.
Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.
Примеры
Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.
Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ<, ВГ, а если при наложении оба конца отрезков совмещаются — значит, они равны.
Теперь рассмотрим сравнение отрезков путем измерения. При помощи линейки вычисляем длину каждого отрезка. Например, длина AB = 2 см, а CD = 8 см. 8>,2, значит, CD>,AB, то есть отрезок CD длиннее AB.
Отрезок
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
Свойства длин отрезков:
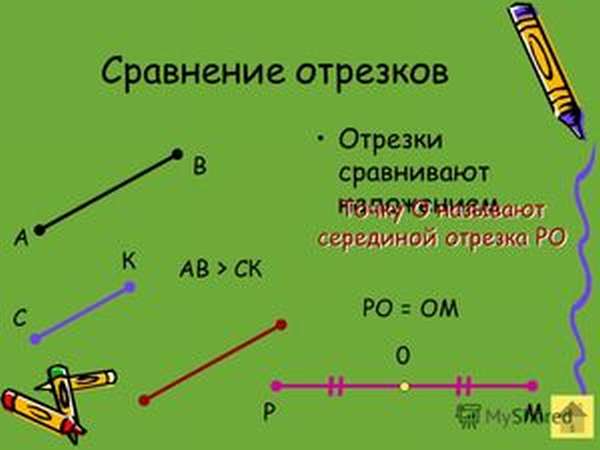
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.
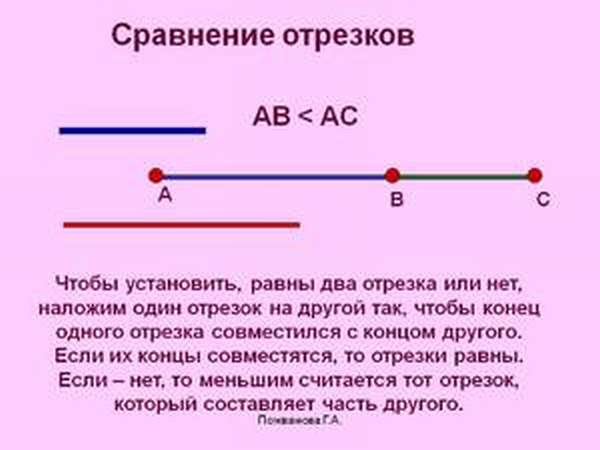
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB Пример. Сравнить длину отрезков AB и AC.
Так как отрезок AB имеет большую длину, чем отрезок AC, то
Так как отрезки AB и AC имеют одинаковую длину, то
Если при измерении отрезков их длины равны, то и отрезки равны.
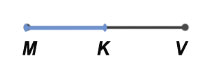
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.