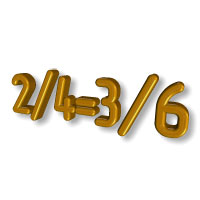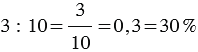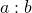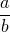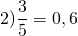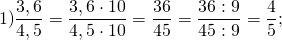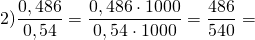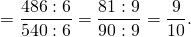Что значит относится в математике
Отношения и пропорции
В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления.
Таким образом, сам смысл термина «отношение» был несколько иной, чем термина «деление»: дело в том, что второй означал разделение определенной именованной величины на любое совершенно отвлеченное абстрактное число. В современной математике понятия «деление» и «отношение» по своему смыслу абсолютно идентичны и являются синонимами. Например, и тот, и другой термин с одинаковым успехом применяют для отношения величин, являющихся неоднородными: массы и объема, расстояния и времени и т.п. При этом многие отношения величин однородных принято выражать в процентах.
В супермаркете насчитывается четыреста наименований различных товаров. Из них двести произведено на территории Российской Федерации. Определить, каково отношение отечественных товаров к общему числу товаров, продаваемых в супермаркете?
400 – общее число товара
Ответ: двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов.
200 : 400 = 0,5 или 50%
В математике делимым принято называть предыдущий член отношения, а делителем – последующий член отношения. В приведенном выше примере предыдущим членом являлось число двести, а последующим – число четыреста.
Два равных отношения образуют пропорцию
В современной математике принято считать, что пропорцией является два равным между собой отношения. К примеру, если общее количество наименований товаров, продаваемых в одном супермаркете, – четыреста, а в России из них произведено двести, а те же значения для другого супермаркета составляют шестьсот и триста, то соотношение количества российских товаров к общему их числу, реализовываемых в обеих торговых предприятиях, одинаково:
1.Двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов
200 : 400 = 0,5 или 50%
2.Триста разделить на шестьсот равняется ноль целых пять десятых, то есть пятьдесят процентов
300 : 600 = 0,5 или 50%
В данном случае имеется пропорция, которую можно записать следующим образом:
Если формулировать это выражение так, как это принято делать в математике, то говорится, что двести относится к четыремстам так же, как триста относится к шестистам. При этом двести и шестьсот называются крайними членами пропорции, а четыреста и триста – средними членами пропорции.
Произведение средних членов пропорции
Согласно одному из законов математики, произведение средних членов любой пропорции равняется произведению ее крайних членов. Если возвратиться к приведенным выше примерам, то проиллюстрировать это можно следующим образом:
Двести умноженное на шестьсот равняется сто двадцать тысяч;
Триста умноженное на четыреста равняется сто двадцать тысяч.
Из этого следует, что любой из крайних членов пропорции равен произведению ее средних членов, деленному на другой крайний член. По тому же самому принципу каждый из средних членов пропорции равен крайних ее членов, деленному на другой средний член.
Если вернуться к приведенному выше примеру пропорции, то:
Двести равняется четыреста умноженное на триста и деленное на шестьсот.
Эти свойства широко используются в практических математических вычислениях тогда, когда требуется найти значение неизвестного члена пропорции при известных значениях трех членов остальных.
Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Частное двух чисел  и и  , отличных от нуля, называют отношением чисел , отличных от нуля, называют отношением чисел  и и  , или отношением числа , или отношением числа  к числу к числу  . . |
Где 



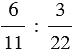
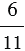
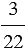
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел 





Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел 



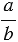
Основное свойство отношения:
| Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю. |
Запишем отношение числа 3 к числу 10 и найдем его значение:
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
Дроби 

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
| Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана). |
Пусть на карте задан масштаб 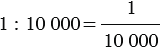
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через 

5 : 
Решаем данное уравнение:



50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через 


Решаем данное уравнение:


0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Поделись с друзьями в социальных сетях:
Что такое отношение чисел
Здесь мы обсудим, что такое отношение чисел и что показывает отношение двух чисел.
Отношение чисел можно записать двумя способами: с помощью знака деления либо с помощью дроби:
Читают: «отношение a к b».
Числа a и b называют членами отношения.
a — предыдущий член отношения, b — последующий член отношения. a и b должны быть отличны от нуля.
2. Отношения используют для сравнения двух величин.
Примеры отношения чисел:
Отношение 120:3 показывает, что 120 в сорок раз больше 3.
Отношение 3/5 показывает, что 3 составляет 0,6 от 5.
3. Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, отличное от нуля.
(основное свойство отношения вытекает из основного свойства дроби ).
Таким образом, отношение дробных чисел можно заменить отношением целых чисел.
4. Примеры отношения величин.
— скорость (отношение пройденного пути ко времени, за которое путь был пройден);
— производительность труда (отношение объема работы ко времени, за которое выполняется работа);
— цена ( отношение стоимости товара к количеству единиц);
— масштаб (отношение длины отрезка на карте к расстоянию между соответствующими точками на местности);
— урожайность (отношение массы собранного урожая к общей площади полей, с которой был собран урожай).
Далее мы рассмотрим равенство двух отношений и его практическое применение.
11 Comments
Ужс…по таким темам у меня 6 классе колы по кд-шкам.
Видимо, я слишком тупа для этой темы >. Светлана Иванова 23.08.2017 06:21 Ответить
Не так много людей, которые понимают тему с первого раза. Попробуйте вернуться к ней еще пару раз, и прояснится.
Добрый вечер,
У вас там описка в первом примере : 4/5
Нет?
С уважением
Да, была опечатка. Спасибо, Марк!
Я это понял сразу (после пары подзатыльников от отца)!! Подача отличная, в 6 кл просто изи учиться!!
мне не суждено понимать
Не святые горшки обжигают. Понять математику не так уж и сложно, было бы желание и трудолюбие.
А как из отношения число сделать?
Разделить первое число на другое. Например, 6:5=1,2.
Равенство и неравенство. Знаки: больше, меньше, равно
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
Что такое пропорция
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
a и d — крайние члены пропорции
Читается это выражение так: a так относится к b, как c относится к d
Например:
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d = a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Примеры решения задач с пропорцией
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4