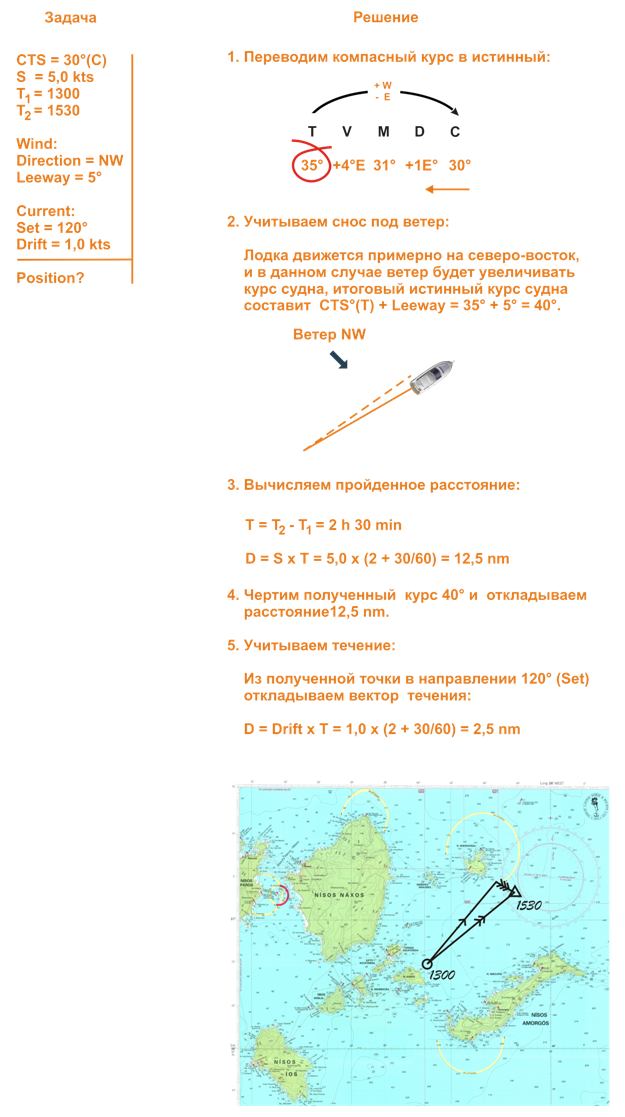
Что значит относительно воды

Скорость судна относительно воды

Скорость судна относительно воды требуется для решения задач, связанных с предупреждением столкновения судов в море, то есть для соблюдения судном Международных Правил Предупреждения Столкновения Судов в море – МППСС-72.

Для этого к радиолокатору должен быть подключен лаг. Заметим, что от приемника GPS в радиолокатор поступают данные о скорости судна относительно грунта.

Рассмотрим разницу между изображениями на экране радиолокатора при вводе данных скорости относительно воды (Speed Through Water — STW) и скорости относительно грунта (Speed over Ground — SOG).

Данные радиолокатора: Стабилизация по Норду (North Up — NU), режим относительного движения (Relative motion — RM), шкала дальности 6 миль (6 NM — Nautical Miles).

Действует сильное Западное течение. Западное, означает движение воды с востока на запад, так как течение «вытекает из компаса».

Судно следует курсом по гирокомпасу 0°. Под действием течения судно имеет сильный дрейф влево и его фактический курс относительно грунта составляет 325°

Встречное судно находится прямо по курсу и следует курсом 180°. Под действием течения судно имеет сильный дрейф вправо и его фактический курс относительно грунта составляет 210°.

На изображении слева, скорость судна относительно воды (STW), и взаимное перемещение судов отображается также, как оно наблюдается визуально, если конечно позволяет видимость. Ситуация сближения судов, идущих прямо или почти прямо друг на друга распознается одинаково и визуально и на экране радиолокатора. Применение правила 14 МППСС — 72 очевидно.

На изображении справа, скорость судна относительно грунта (SOG), и взаимное перемещение судов отличается от наблюдаемого визуально. На экране радиолокатора наблюдатель видит ситуацию, когда суда идут пересекающимися курсами. Ошибочно может трактоваться необходимость применения правила 15.

И в том и в другом случае дистанция кратчайшего сближения (CPA) и время кратчайшего сближения (TCPA) одни и те же.

Отличие только в возможной оценке ситуации и взаимных обязанностей судов. Как следствие, может быть выполнен маневр, не соответствующий правилам МППСС-72.

Именно для того, чтобы исключить возможную двусмысленность оценки ситуации и установлено требование использовать скорость относительно воды для решения задач связанных с предупреждением столкновения судов.

Источник

Относительность движения

Любое движение тела происходит по отношению к другим телам. Физики говорят: «Относительно других тел».

К примеру, человек, едущий в автобусе, относительно автобуса находится в состоянии покоя, а относительно дороги – движется.

Примечание: Когда мы рассматриваем движение тела, мы выбираем систему отсчета, в которой это дело будет двигаться. При этом, тело отсчета мы принимаем за неподвижное тело, относительно которого происходит движение изучаемого тела.

в разных системах отсчета (СО) будут различаться.

Траектория тела различна в разных системах отсчета

Траектория – это относительная характеристика движения. Потому, что она различается для разных систем отсчета (СО).

В то время, пока самолет летит, точка, лежащая на кончике его винта, относительно самолета движется по окружности (рис. 1), а относительно неподвижного наблюдателя на земле – эта же точка имеет винтовую траекторию.

Например, движение ниппеля велосипедного колеса во время поездки на велосипеде.

В системе отсчета, связанной с:

Что такое циклоида

Циклоида – это плоская кривая линия. По такой линии движется точка, лежащая на окружности, когда эта окружность катится по прямой без проскальзывания (рис. 2).

Циклоиду называют трансцендентной кривой линией.

Линия трансцендентная, если ее в прямоугольных координатах не получается описать с помощью алгебраического уравнения.

Но с помощью параметра t можно записать отдельно координату x и координату y с помощью таких уравнений:

\[ \large \begin x = r \cdot t — r \cdot sin(t) \\ y = r — r \cdot cos(t) \end \]

Примечания:

Циклоиду впервые изучил Галилео Галилей. Этот выдающийся итальянский ученый занимался физикой, математикой, астрономией, механикой и философией.

А английский математик и архитектор Кристофер Рен в 1658 году посчитал длину арки циклоиды.

Длина циклоиды равна четырем диаметрам производящей окружности.

Кристофер Рен спроектировал и руководил возведением в Лондоне купола собора Святого Павла.

С помощью циклоиды братья Бернулли решили задачу о скорейшем спуске — брахистохроне. Брахистохрон – с греч. «Краткое время». Они доказали, что по желобу, имеющему форму перевернутой вниз циклоиды шарик скатывается вниз за кратчайшее из возможных время.

Скорость тела различна в разных системах отсчета

Рассмотрим движение человека в едущем по прямому участку пути трамвае (рис. 3).

Скорость трамвая \(\large \vec>>\) 60 километров в час. Предположим, в движущемся вагоне трамвая человек перемещается от задней части трамвая к его передней части, со скоростью \(\large \vec>>\) 3 километра в час.

Тогда скорость человека относительно трамвая будет равна 3 километрам в час, а относительно земли – 63 километрам в час.

Как переходить из одной системы отсчета в другую

Любое движение, которое мы рассматриваем, а, так же, его характеристики, будут различаться в разных системах отсчета.

Относительно одних тел рассматриваемое тело может покоиться, а вместе с тем, относительно других тел оно может находиться в движении.

Чтобы осуществить переход между системами отсчета, нужно применять закон сложения скоростей и перемещений. Скорость и перемещение – это векторы. Значит, будем складывать их геометрически. То есть, при сложении векторов будем учитывать их направления.

Примечание: Ньютон изучал движение тел. В его теории время протекает одинаково во всех системах отсчета. То есть, в механике Ньютона время – это абсолютная величина.

Представим себе такую картину: На берегу реки сидит и отдыхает девушка (рис. 4). По реке мимо нее проплывает плот (по течению). С плота в это время в воду прыгает молодой человек и вплавь добирается к противоположному берегу реки. После чего, садится на берег и отдыхает.

Перемещение в различных системах отсчета

Сначала запишем перемещение парня в системе отсчета, связанной с девушкой, когда нам известны его перемещение в системе отсчета, связанной с плотом.

Примечание:

На рисунке перемещение плота и перемещение парня относительно плота обозначены длинными черными стрелками. А перемещение парня относительно сидящей на берегу девушки обозначено длинной синей стрелкой.

Из рисунка видно, что векторы перемещений образуют прямоугольный треугольник.

Сложив вектор переносного и относительного перемещений, получим вектор абсолютного перемещения:

\( \large \overrightarrow>> \) – вектор перемещения плота;

\( \large \overrightarrow>> \) – вектор перемещения парня относительно плота (собственное перемещение парня);

\( \large \overrightarrow>> \) – вектор перемещения парня относительно девушки на берегу;

Длину вектора абсолютного перемещения можно найти по теореме Пифагора:

Скорость в различных системах отсчета

Запишем еще раз формулу для связи перемещений:

Зная перемещение, и время равномерного движения, можно найти модуль вектора скорости, т. е. длину вектора скорости.

Скорость плывущего плота и скорость парня не изменяются. Поэтому, для связи скорости и перемещения можно применить формулу

Разделив обе части этого уравнения на время t, получим выражение для скорости равномерного движения:

Обе части уравнения для перемещений разделим на время t движения.

Полученное выражение можно записать с помощью векторов скоростей:

В частности, на рисунке 4 красными векторами обозначены скорость реки (плота) и скорость парня.

Опишем обозначения, использованные нами в уравнении, связывающем скорости в различных системах отсчета:

\( \large \overrightarrow>> = \overrightarrow>> \) – вектор скорости парня;

\( \large \overrightarrow>> = \overrightarrow>> \) – вектор скорости плота (течения реки);

\( \large \overrightarrow>> \) – вектор скорости парня относительно девушки;

Длину вектора скорости найдем по теореме Пифагора:

Таким образом, до прыжка в воду скорость парня в системе отсчета, связанной с плотом, равнялась нулю (рис. 5).

А в системе отсчета, связанной с отдыхающей на берегу девушкой, скорость парня равнялась скорости течения реки (скорости плота).

После прыжка с плота в системе отсчета, связанной с плотом, скорость парня равняется скорости, с которой он плывет к берегу перпендикулярно течению реки.

Ну а в системе отсчета, связанной с девушкой, скорость парня – это векторная сумма скорости течения реки и скорости плавания парня.

Источник

Что значит относительно воды

Скорость течения широкой реки 3,6 км/ч. Под каким углом к направлению течения реки лодочник должен направлять лодку, скорость которой относительно воды равна 2 м/с, чтобы за 15 минут её снесло по направлению течения на 1,8 км?

При движении под углом к течению реки, лодка будет двигаться по реке со скоростью

Тогда за время лодка переместится на расстояние

Лодочник должен направлять лодку под углом 60° к направлению реки.