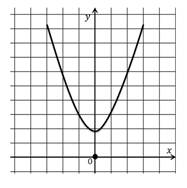
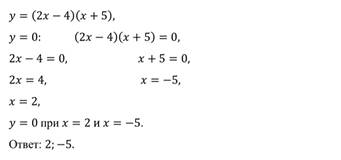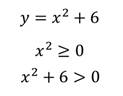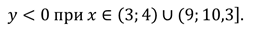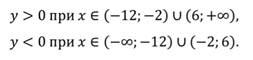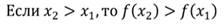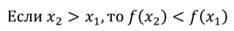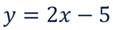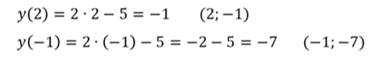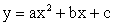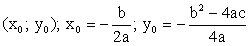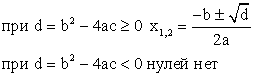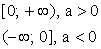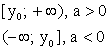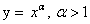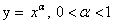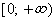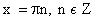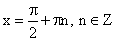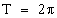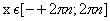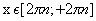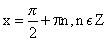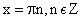Что значит описать свойства функции

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.

теория по математике 📈 функции

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Таким образом, мы нашли нуль функции: х=2

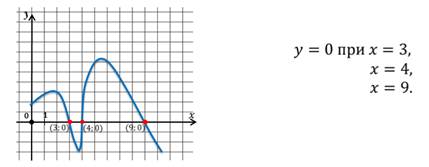
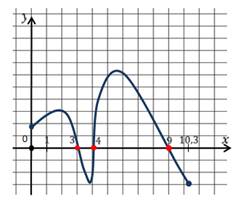
Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

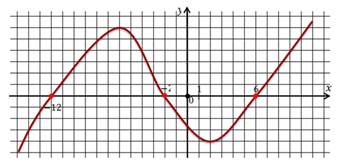
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

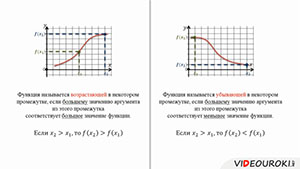
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Источник

Свойства функций

Урок 2. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Свойства функций»

На прошлом уроке мы с вами изучили понятие функция. Изучили её график и научились находить область определения и область значений функции.

· промежутки знакопостоянства функции;

· промежутки монотонности функции.

Нулями функции называют такие значения аргумента, при которых функция равна нулю.

В данном случае функция задана графически и мы определили нули функции по графику. Так же нули функции можно находить по формуле, с помощью которой задана функция.

Решив уравнение, мы найдём те значения х, при которых функция равна нулю.

Стоит обратить внимание на то, что не каждая функция имеет нули.

График не пересекает ось икс ни в одной точке.

Промежутки знакопостоянства функции

Функция принимает положительные значения:

И отрицательные значения:

Запишите промежутки знакопостоянства функции:

Положительные и отрицательные значения функции:

Промежутки монотонности функции

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.

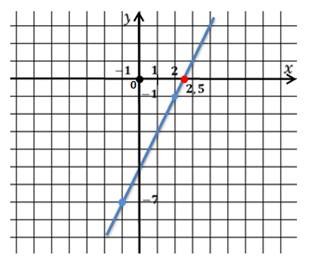
Опишем свойства функции:

Графиком является прямая, поэтому для построения достаточно двух точек:

Найдём значения функции:

Областью определения и областью значений будет множество всех действительных чисел. Ведь х и у могут быть любыми числами.

Источник

Что значит описать свойства функции

Функция

Область определения

Вершина параболы

Нули функции

Экстремумы

если a 0, то максимум в вершине

Область значений

Четность

ни четная, ни нечетная

Функция

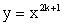
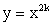
Область определения

Область значений

Четность

Нули функции

Экстремумы

х = 0 — точка минимума

Монотонность

возрастает при х ϵ R

при х ≤ 0 убывает
при х > 0 возрастает

Функция

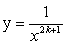
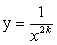
Область определения

Область значений

Четность

Нули функции

Экстремумы

Монотонность

Функция

Область определения

Область значений

Нули функции

Экстремумы

Монотонность

возрастает при х ϵ D(f)

возрастает при х ϵ D(f)

Функция

Область определения

Область значений

Нули функции

Экстремумы

Монотонность

убывает при х ϵ D ( f )

возрастает при х ϵ D ( f )

Функция

Область определения

Область значений

Нули функции

Экстремумы

Монотонность

убывает при х ϵ D ( f )

возрастает при х ϵ D ( f )

Функция

Область определения

Область значений

Нули функции

Четность

Периодичность

Экстремумы

Монотонность

Функция

Область определения

R кроме

R кроме

Источник

Определение и свойства функций

Содержание:

Определение и свойства функций

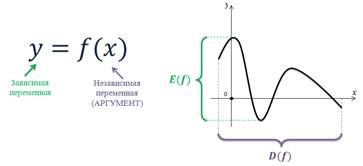
Если даны числовое множество X и правило f, позволяющее поставить в соответствие каждому элементу х из множества X определенное число у, то говорят, что задана функция у = f(x) с областью определения X; пишут:

При этом переменную х называют независимой переменной или аргументом, а переменную у — зависимой переменной. Для области определения функции используют также обозначение D (f). Множество всех значений функции у = f(x), , называют областью значений функции и обозначают E(f).

Если функция задана выражением, то допускается ее задание в виде у = f(x) без условия в случае, когда область определения выражения f(x) совпадает с областью определения функции.

Например, запись «функция » означает поскольку область определения выражения задается неравенством

Аналитическое задание функции

Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f(x), где f(x) — некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.

Пример 1.

Область определения этой функции — луч Чтобы найти значение функции в любой точке достаточно найти числовое значение выражения в выбранной точке. Функция задана аналитически.

Пример 2.

Функция у = f(ж) задана аналитически формулой Найти:

Решение:

а) Чтобы найти f(-x), надо в f(x) всюду вместо х подставить (-х). Получим

Пример 3.

Найти область определения функции

Решение:

Пример 4.

Найти область определения функции

Решение:

Выражение определено при тех х, при которых т. е. при Значит, область определения функции — луч

Иногда функция задается на различных промежутках различными формулами. Такую функцию называют кусочной.

Пример 5.

Эта функция определена на отрезке [-1; 1]. Для вычисления ее значений нужно точно определить, какой формулой следует воспользоваться для заданного конкретного значения аргумента. Например, если нужно вычислить f(0,5), воспользуемся равенством f(x) = х + 2 (поскольку число х = 0,5 удовлетворяет условию ) и получим f(0,5) = 2,5. Если же нужно вычислить f(-0,5), то воспользуемся равенством f(x) = 2х + 3 (поскольку число х = 0,5 удовлетворяет условию ) и получим f(-0,5) = 2.

Табличное задание функции

На практике часто используют табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов, таблица квадратных корней.

Во многих случаях табличное задание функции оказывается удобным. Оно позволяет найти значения функции для значений аргумента, имеющихся в таблице, без всяких вычислений. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае одной величине придают определенные значения, а потом из опыта для каждого из таких значений находят значение (обычно приближенное) второй величины. Таким образом, опыт позволяет составить некоторую таблицу значений функции. Существуют методы, позволяющие по такой таблице подбирать формулы, задающие функции (с определенной точностью).

Числовая плоскость. Координатная плоскость, оси координат

Множество всех пар (Под парой чисел понимают два числа, которые рассматриваются в определенном порядке.) действительных чисел называют числовой плоскостью.

Как для множества всех действительных чисел есть геометрическая модель — координатная прямая (см. п. 21), так и для множества всех пар действительных чисел есть геометрическая модель — координатная плоскость.

Координатная плоскость ху определяется двумя взаимно перпендикулярными координатными прямыми с общим началом О и одинаковым масштабом (рис. 1.7). Точка О — начало координат. Горизонтальную прямую называют осью абсцисс или осью х, вертикальную — осью ординат или осью у.

Если отметить на координатной плоскости все точки с абсциссой , то получится прямая, параллельная оси у (рис. 1.7); говорят, что — уравнение этой прямой. Если отметить на координатной плоскости все точки с ординатой , то получится прямая, параллельная оси х (рис. 1.7); говорят, что — уравнение этой прямой.

О координатной плоскости см. также «Геометрия», п. 101.

График функции, заданной аналитически

Пусть функция задана аналитически формулой у = f(x). Если на координатной плоскости отметить все точки, обладающие следующим свойством: абсцисса точки принадлежит области определения функции, а ордината равна соответствующему значению функции, — то получится множество точек (х; f(x)) — график функции.

Например, графиком функции у = х является множество точек вида (х; х), т. е. точек, имеющих одинаковые координаты. Это множество точек есть биссектриса координатных углов I и III (рис. 1.8).

На практике для построения графика функции составляют таблицу значений функции при некоторых значениях аргумента, наносят на плоскость соответствующие точки и соединяют полученные точки линией. При этом предполагают, что найденные точки достаточно точно показывают ход изменения функции.

Пример 6.

Построить график функции

Решение:

Составим таблицу некоторых значений функции:

Нанесем найденные точки (0; 0); (0,5; 0,25); (-0,5; 0,25); (1; 1); (-1; 1); (2; 4); (-2; 4); (3; 9); (-3; 9) на координатную плоскость (рис. 1.9). Соединив эти точки плавной линией, получим график (а точнее, эскиз графика) функции (рис. 1.10). Эту линию называют параболой. Вообще параболой является график любой функции вида (см. п. 111).

Четные и нечетные функции

Функцию у = f(x), , называют четной, если для любого х из области определения функции выполняется равенство f(-x) = f(x).

Например, — четные функции, а — нечетные функции.

Из определения следует, что область определения X как четной, так и нечетной функции должна обладать следующим свойством: если , то и (т. е. X — симметричное относительно О множество).

Пример 7.

Исследовать на четность функции:

Решение:

а) Имеем Значит, для всех х. Функция является четной.

б) Имеем Значит, для всех х. Функция является нечетной.

в) Имеем Заметим, что Не выполняется ни равенство ни равенство Значит, функция не является ни четной, ни нечетной.

График четной функции. График нечетной функции

Графики четной и нечетной функций обладают следующими особенностями:

Если функция является четной, то ее график симметричен относительно оси ординат.

Если функция является нечетной, то ее график симметричен относительно начала координат.

Пример 8.

Построить график функции

Решение. Имеем Значит, функция четна, а потому ее график симметричен относительно оси ординат.

Если Графиком функции у = х при служит биссектриса первого координатного угла. Подвергнув ее преобразованию симметрии относительно оси у, получим график функции (рис. 1.11).

Пример 9.

Построить график функции

Решение:

Имеем Значит, функция нечетна, а потому график ее симметричен относительно начала координат.

Если Значит, при имеем Графиком будет ветвь параболы. Она изображена на рисунке 1.12. Подвергнув ее преобразованию симметрии относительно начала координат, получим график функции (рис. 1.13).

Периодические функции

Число Т называют периодом функции у = f(x).

Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом.

Примеры периодических функций с основным периодом:

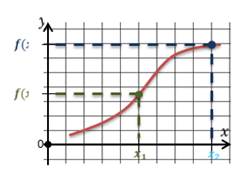
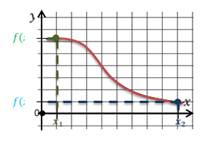
Монотонные функции

Функцию у = f(x), , называют возрастающей на промежутке ( — знак включения одного множества в другое), если для любых выполняется неравенство

Функцию у = f(x), , называют убывающей на промежутке , если для любых выполняется неравенство

Иными словами, функция возрастает (убывает) на промежутке, если, какие бы два значения аргумента, принадлежащие этому промежутку, ни взять, окажется, что большему значению аргумента соответствует большее (меньшее) значение функции.

При движении вдоль оси абсцисс слева направо ордината графика возрастающей функции увеличивается (рис. 1.15), а ордината графика убывающей функции уменьшается (рис. 1.16).

Возрастающие и убывающие функции объединяют термином «монотонные функции».

Пример 10.

Исследовать на монотонность функцию

Решение:

Пусть . Тогда по свойствам числовых неравенств (см. п. 24) имеем ,

Итак, , а это значит, что функция возрастает на всей числовой прямой.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник