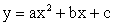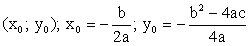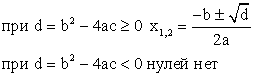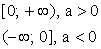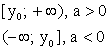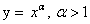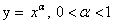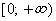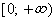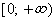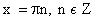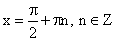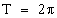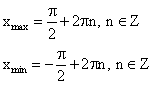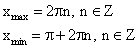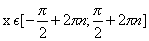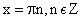Что значит описать график функции
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
область определения выглядит так
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке: 
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции 
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции 
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины 
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции 
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б) 
г) 
д) 
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а) 
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г) 
Преобразование в одно действие типа 
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д) 
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Что значит описать график функции
Функция
Область определения
Вершина параболы
Нули функции
Экстремумы
если a 0, то максимум в вершине
Область значений
Четность
ни четная, ни нечетная
Функция
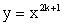
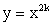
Область определения
Область значений
Четность
Нули функции
Экстремумы
х = 0 — точка минимума
Монотонность
возрастает при х ϵ R
при х ≤ 0 убывает
при х > 0 возрастает
Функция
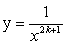
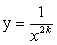
Область определения
Область значений
Четность
Нули функции
Экстремумы
Монотонность
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
возрастает при х ϵ D(f)
возрастает при х ϵ D(f)
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Четность
Периодичность
Экстремумы
Монотонность
Функция
Область определения
R кроме 
R кроме 
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Парабола
Гипербола
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>
Если k 0, ветви гиперболы проходят через II и IV четверти.
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Свойства функции
В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое числовая функция и какие свойства функции необходимо знать и уметь исследовать.
Что такое числовая функция? Пусть у нас есть два числовых множества: Х и Y, и между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие единственный элемент y из множества Y.
Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y. 
Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией.
Множество Х называется областью определения функции.
Множество Y называется множеством значений значений функции.
Равенство 
называется уравнением функции. В этом уравнении 
— независимая переменная, или аргумент функции. 
— зависимая переменная.
Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.
Основные свойства функций.
1. Область определения функции.
Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции имеет смысл. Другими словами, это область допустимых значений выражения 
.
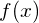
Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
2. Множество значений функции.
Множество значений функции Е(y)— это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
Чтобы найти нули функции , нужно решить уравнение 
. Корни этого уравнения и будут нулями функции .
Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции .
4. Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть 
или 
.
Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и .
Чтобы найти промежутки знакопостоянства функции по ее графику, нужно
5. Промежутки монотонности функции.
Промежутки монотонности функции — это такие промежутки значений аргумента х, при которых функция возрастает или убывает.
Говорят, что функция возрастает на промежутке I, если для любых двух значений аргумента 
, принадлежащих промежутку I таких, что 
выполняется соотношение: 
.
Другими словами, функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.
Говорят, что функция убывает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: 
.
Другими словами, функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.
6. Точки максимума и минимума функции.
Точка 
называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
.
Графически это означает что точка с абсциссой x_0 лежит выше других точек из окрестности I графика функции y=f(x).
Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
Графически это означает что точка с абсциссой лежит ниже других точек из окрестности I графика функции .
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
7. Четность (нечетность) функции.
Функция называется четной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, 
также принадлежит области определения функции.
Другими словами, область определения четной функции симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение 
.
Функция называется нечетной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, 
также принадлежит области определения функции.
Другими словами, область определения нечетной функции 
симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение 
.
Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.
Чтобы определить четность функции, нужно:
а). Найти область определения функции , и определить, является ли она симметричным множеством.
Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.
Если область определения функции — симметричное множество, то проверяем п. б)
Если , то функция четная.
Если , то функция нечетная.
Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.
График четной функции симметричен относительно оси ординат ( прямой OY ).
График нечетной функции симметричен относительно начала координат ( точки (0,0) ).
8. Периодичность функции.
Функция называется периодической, если существует такое положительное число Т, что
В программе средней школы из числа периодических функций изучают только тригонометрические функции.
Предлагаю вам посмотреть ВИДЕОУРОК, в котором я рассказываю, как определить свойства функции по ее графику.