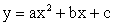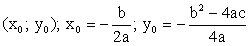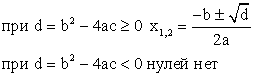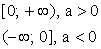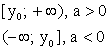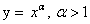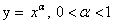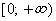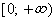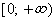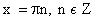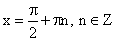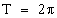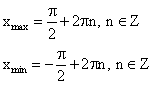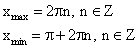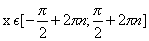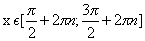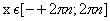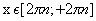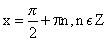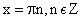Что значит охарактеризовать график функции
Что значит охарактеризовать график функции
Функция
Область определения
Вершина параболы
Нули функции
Экстремумы
если a 0, то максимум в вершине
Область значений
Четность
ни четная, ни нечетная
Функция
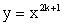
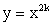
Область определения
Область значений
Четность
Нули функции
Экстремумы
х = 0 — точка минимума
Монотонность
возрастает при х ϵ R
при х ≤ 0 убывает
при х > 0 возрастает
Функция
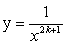
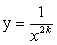
Область определения
Область значений
Четность
Нули функции
Экстремумы
Монотонность
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
возрастает при х ϵ D(f)
возрастает при х ϵ D(f)
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Четность
Периодичность
Экстремумы
Монотонность
Функция
Область определения
R кроме 
R кроме 
Основные элементарные функции: их свойства и графики
Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.
Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.
Выделяют следующие виды основных элементарных функций:
Постоянная функция
Свойства постоянных функций:
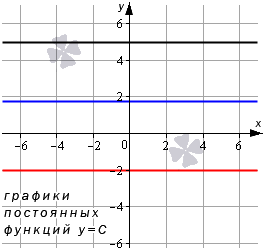
Корень n-й степени
Данная элементарная функция определяется формулой y = x n ( n – натуральное число больше единицы).
Рассмотрим две вариации функции.
Похожий вид у графиков функции четной степени при иных значениях показателя.
Свойства функции корень n-ой степени, n – четное число
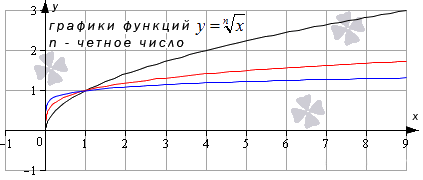
Иные нечетные значения показателя корня функции y = x n дадут график аналогичного вида.
Свойства функции корень n-ой степени, n – нечетное число
Степенная функция
Вид графиков и свойства функции зависят от значения показателя степени.
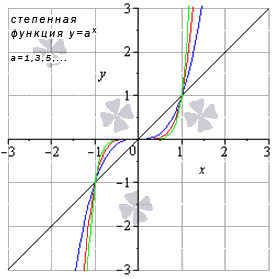
Степенная функция при нечетном положительном показателе
Свойства степенной функции, когда показатель степени – нечетный положительный
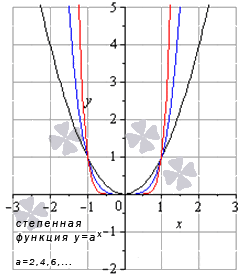
Степенная функция при четном положительном показателе
Свойства степенной функции, когда показатель степени – четный положительный:
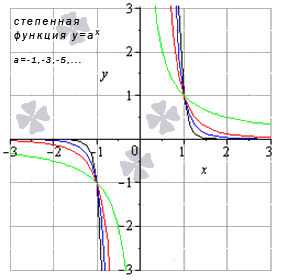
Степенная функция при нечетном отрицательном показателе
Свойства степенной функции, когда показатель степени – нечетный отрицательный:
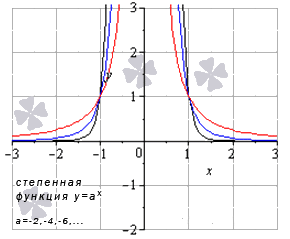
Степенная функция при четном отрицательном показателе степени
Свойства степенной функции, когда показатель степени – четный отрицательный:
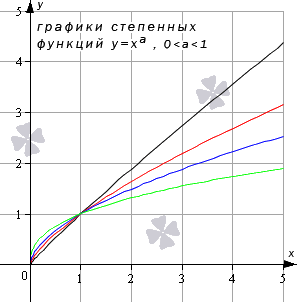
Степенная функция при рациональном или иррациональном показателе (значение больше нуля и меньше единицы)
Иные значения показателя степени a (при условии 0 a 1 ) дадут аналогичный вид графика.
Свойства степенной функции при 0 a 1 :
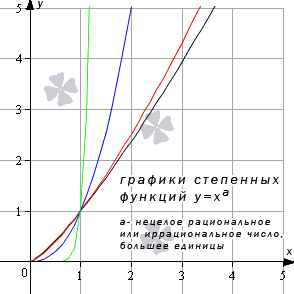
Степенная функция при нецелом рациональном или иррациональном показателе степени (больше единицы)
Иные значения показателя степени а при условии a > 1 дадут похожий вид графика.
Свойства степенной функции при a > 1 :
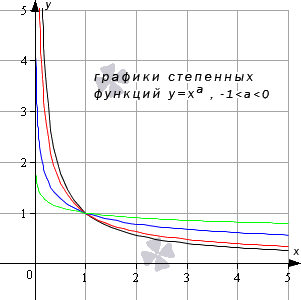
Степенная функция при действительном показателе степени (больше минус единицы и меньше нуля)
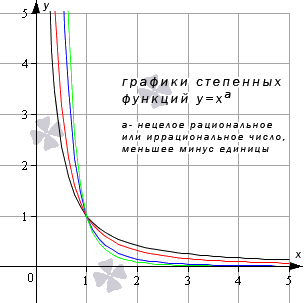
Степенная функция при нецелом действительном показателе степени (меньше минус единицы)
Показательная функция
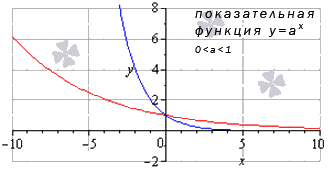
Сначала разберем ситуацию, когда основание показательной функции имеет значение от нуля до единицы ( 0 a 1 ) . Наглядным примером послужат графики функций при a = 1 2 (синий цвет кривой) и a = 5 6 (красный цвет кривой).
Свойства показательной функции, когда основание меньше единицы:
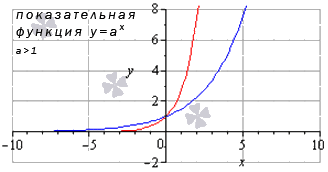
Проиллюстрируем этот частный случай графиком показательных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет графика).
Иные значения основания, большие единицы, дадут аналогичный вид графика показательной функции.
Свойства показательной функции, когда основание больше единицы:
Логарифмическая функция
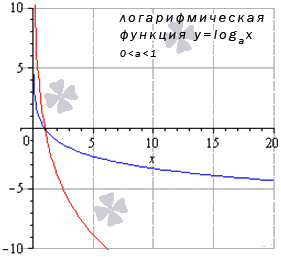
График логарифмической функции имеет различный вид, исходя из значения основания а.
Иные значения основания, не большие единицы, дадут аналогичный вид графика.
Свойства логарифмической функции, когда основание меньше единицы:
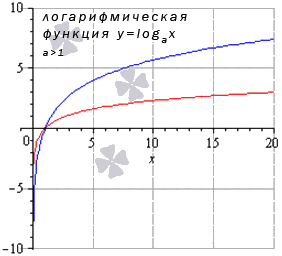
Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а > 1 . На чертеже ниже – графики логарифмических функций y = log 3 2 x и y = ln x (синий и красный цвета графиков соответственно).
Иные значения основания больше единицы дадут аналогичный вид графика.
Свойства логарифмической функции, когда основание больше единицы:
Тригонометрические функции, их свойства и графики
Тригонометрические функции – это синус, косинус, тангенс и котангенс. Разберем свойства каждой из них и соответствующие графики.
В общем для всех тригонометрических функций характерно свойство периодичности, т.е. когда значения функций повторяются при разных значениях аргумента, отличающихся друг от друга на величину периода f ( x + T ) = f ( x ) ( T – период). Таким образом, в списке свойств тригонометрических функций добавляется пункт «наименьший положительный период». Помимо этого, будем указывать такие значения аргумента, при которых соответствующая функция обращается в нуль.
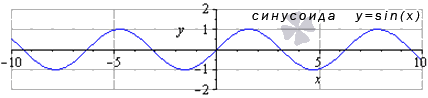
График данной функции называется синусоида.
Свойства функции синус:
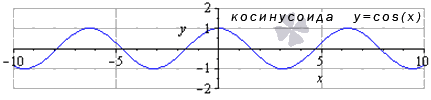
График данной функции называется косинусоида.
Свойства функции косинус:
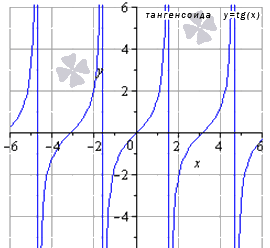
График данной функции называется тангенсоида.
Свойства функции тангенс:
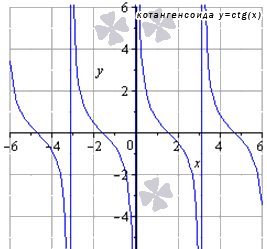
График данной функции называется котангенсоида.
Свойства функции котангенс:
Обратные тригонометрические функции, их свойства и графики
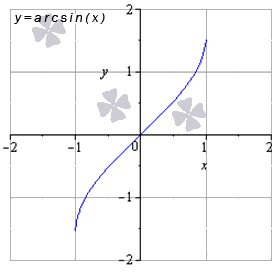
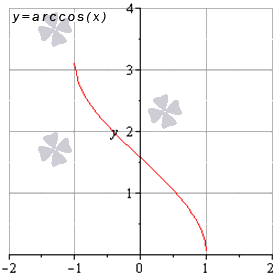
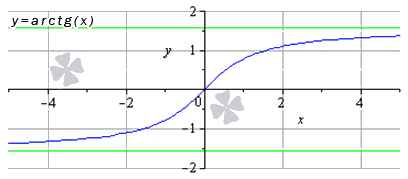
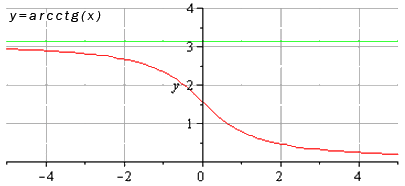
Обратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс. Зачастую, в связи с наличием приставки «арк» в названии, обратные тригонометрические функции называют аркфункциями.
Свойства функции арксинус:
Свойства функции арккосинус:
Свойства функции арктангенс:
Свойства функции арккотангенс:
Свойства функции
В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое числовая функция и какие свойства функции необходимо знать и уметь исследовать.
Что такое числовая функция? Пусть у нас есть два числовых множества: Х и Y, и между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие единственный элемент y из множества Y.
Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y. 
Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией.
Множество Х называется областью определения функции.
Множество Y называется множеством значений значений функции.
Равенство 
называется уравнением функции. В этом уравнении 
— независимая переменная, или аргумент функции. 
— зависимая переменная.
Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.
Основные свойства функций.
1. Область определения функции.
Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции имеет смысл. Другими словами, это область допустимых значений выражения 
.
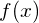
Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
2. Множество значений функции.
Множество значений функции Е(y)— это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
Чтобы найти нули функции , нужно решить уравнение 
. Корни этого уравнения и будут нулями функции .
Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции .
4. Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть 
или 
.
Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и .
Чтобы найти промежутки знакопостоянства функции по ее графику, нужно
5. Промежутки монотонности функции.
Промежутки монотонности функции — это такие промежутки значений аргумента х, при которых функция возрастает или убывает.
Говорят, что функция возрастает на промежутке I, если для любых двух значений аргумента 
, принадлежащих промежутку I таких, что 
выполняется соотношение: 
.
Другими словами, функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.
Говорят, что функция убывает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: 
.
Другими словами, функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.
6. Точки максимума и минимума функции.
Точка 
называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
.
Графически это означает что точка с абсциссой x_0 лежит выше других точек из окрестности I графика функции y=f(x).
Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
Графически это означает что точка с абсциссой лежит ниже других точек из окрестности I графика функции .
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
7. Четность (нечетность) функции.
Функция называется четной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, 
также принадлежит области определения функции.
Другими словами, область определения четной функции симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение 
.
Функция называется нечетной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, 
также принадлежит области определения функции.
Другими словами, область определения нечетной функции 
симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение 
.
Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.
Чтобы определить четность функции, нужно:
а). Найти область определения функции , и определить, является ли она симметричным множеством.
Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.
Если область определения функции — симметричное множество, то проверяем п. б)
Если , то функция четная.
Если , то функция нечетная.
Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.
График четной функции симметричен относительно оси ординат ( прямой OY ).
График нечетной функции симметричен относительно начала координат ( точки (0,0) ).
8. Периодичность функции.
Функция называется периодической, если существует такое положительное число Т, что
В программе средней школы из числа периодических функций изучают только тригонометрические функции.
Предлагаю вам посмотреть ВИДЕОУРОК, в котором я рассказываю, как определить свойства функции по ее графику.