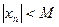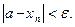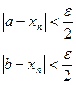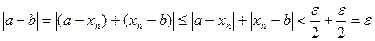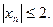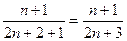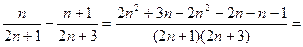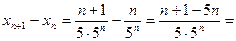Что значит ограниченная последовательность

Ограниченные и неограниченные последовательности

Определение. Последовательность n> называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:

т.е. все члены последовательности принадлежат промежутку (-М; M).

Определение. Последовательность (x_n) называется ограниченной сверху, если для любого n существует такое число М, что

Определение. Последовательность n>называется ограниченной снизу, если для любого n существует такое число М, что

Пример. n> = n – ограничена снизу <1, 2, 3,>.

Определение. Число а называется пределом последовательности n>, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие:

Это записывается: lim x_n = a.

В этом случае говорят, что последовательность n> сходится к а при n®¥.

Свойство: Если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim .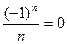

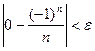
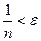
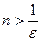
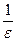
Пусть при n > N верно , т.е. . Это верно при , таким образом, если за N взять целую часть от , то утверждение, приведенное выше, выполняется.

Пример. Показать, что при n®¥ последовательность 3, 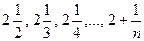имеет пределом число 2.

Очевидно, что существует такое число n, что 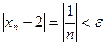, т.е. lim n> = 2.

Теорема. Последовательность не может иметь более одного предела.

Доказательство. Предположим, что последовательность n>имеет два предела a и b, не равные друг другу.

Тогда по определению существует такое число e >0, что

Запишем выражение:

А т.к. e- любое число, то 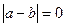, т.е. a = b. Теорема доказана.

Теорема. Если x_n ® a, то .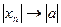

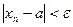
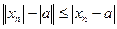
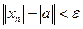
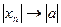
Доказательство. Из x_n ® a следует, что . В то же время:

, т.е. , т.е. . Теорема доказана.

Теорема. Если x_n ® a, то последовательность n> ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательность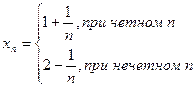не имеет предела, хотя

Монотонные последовательности

Определение:

1) Если x_n+1 > x_n для всех n, то последовательность возрастающая.

2) Если x_n+1 ³ x_n для всех n, то последовательность неубывающая.

n> = n – возрастающая и неограниченная.

Найдем член последовательности n₊₁> =

Найдем знак разности: n>-n₊₁> =

, т.к. nÎN, то знаменатель положительный при любом n.

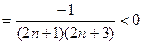
Таким образом, x_n+1 > x_n. Последовательность возрастающая, что и следовало доказать.

Найдем 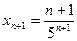. Найдем разность

Источник

Алгебра

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Понятие числовой последовательности

Попытаемся записать в ряд все четные числа, начиная с двойки:

Ясно, что запись можно продолжать бесконечно. Мы получили некоторый ряд чисел, в данном случае бесконечный. Любой такой ряд называется бесконечной числовой последовательностью

Приведем примеры бесконечных числовых послед-тей:

Заметим, что числа в послед-ти могут повторяться. Так, известно, что число π – это бесконечная десятичная дробь 3,1415926… Выписывая в ряд эти цифры, можно получить послед-ть, в которой будут повторяющиеся числа:

Числа, входящие в состав послед-ти, называют членами послед-ти. Всегда можно указать, какое число является первым членом послед-ти, какое – вторым и т. д. Для их обозначения используются буквы с индексами. Например, есть послед-ть четных чисел 2, 4, 6, 8… Выпишем первые ее члены, обозначая их буквой а:

Получается, что каждому натуральному числу n соответствует какой-то единственный член послед-ти, который обозначается как а_n. То есть послед-ть задает некое правило, с помощью которого для каждого числа n можно вычислить число a_n. Отсюда можно сформулировать более сложное определение бесконечной числовой послед-ти – это функция, областью определения которой является множество натуральных чисел.

Способы задания последовательностей

Чтобы задать послед-ть, необходимо указать способ, с помощью которого можно вычислить любой ее член. Проще всего это сделать, записав формулу, в которой в качестве переменной использует номер члена послед-ти n.Такая формула называется формулой n-ого члена последовательности.

Пример. Послед-ть задается формулой а_n = 3n. Выпишите первые пять членов этой послед-ти.

Решение. Чтобы найти первый член послед-ти, то есть а₁, просто подставим в формулу единицу:

Аналогично можно вычислить и следующие четыре члена послед-ти:

Итак, послед-ть имеет вид:

Пример:Запишите формулу n-ого члена для послед-ти

состоящей из положительных нечетных чисел.

Решение. Каждое нечетное число можно представить в виде 2n– 1. Тогда получаем:

Получаются как раз члены послед-ти, указанной в условии. Поэтому формула n-ого члена будет выглядеть как а_n = 2n– 1.

Стоит обратить внимание, что для вычисления n-ого члена послед-ти НЕ нужно вычислять все предшествующие члены.

Пример. Запишите 38-й член послед-ти, заданной формулой а_n = 2n 2 + 1.

Решение. Подставим n = 38 в формулу и получим:

Теперь рассмотрим послед-ть, в которой первые два числа равны единице, а каждый следующий член равен сумме двух предыдущих. Она называется последовательностью Фибоначчи и начинается так:

Действительно, по условию, первые два члена – это единица:

а каждый следующий равен сумме предыдущих:

Формулу n-ого члена записать для послед-ти Фибоначчи очень сложно (хотя и возможно). Вместо этого здесь удобнее использовать рекуррентный способ задания последовательности. Записываются первые несколько членов послед-ти, а после дается формула (ее называют рекуррентной), которая позволяет вычислить следующие члены по предыдущим:

При использовании рекуррентного способа для вычисления n-ого члена обычно необходимо вычислить все предыдущие члены послед-ти.

Пример. Найдите пятый член послед-ти, заданной рекуррентной формулой а_n= 3•а_n–1– 1, если а₁ = 2.

Решение. Будем последовательно вычислять все члены послед-ти, вплоть до пятого:

Надо понимать, что одну и ту же послед-ть можно задать по-разному. Так, послед-ть четных чисел можно задать формулой n-ого члена а_n = 2n, так и рекуррентной формулой а_n = a_n–1 + 2, если а₁ = 1.

Решение. Сначала вычислим первый член послед-ти:

Чтобы записать рекуррентную формулу, попытаемся найти разницу между членами, имеющими номера n и (n– 1):

Итак, получили равенство

Перенесем в нем слагаемое (– a_{n– 1}) вправо и получим рекуррентную формулу:

Наконец, некоторые послед-тине получается задать ни формулой n-ого члена, ни рекуррентным способом. Их можно только описать. Таковой является, например, послед-ть простых чисел:

Мы не будем это доказывать, однако не существует такой формулы, которая позволяла бы вычислить n-ое простое число либо по самому числу n, либо по предыдущим простым числам. Действительно, для построения такой послед-ти используют особый алгоритм, известный как решето Эратосфена. Если бы существовала формула n-ого члена, то потребность в использовании решета Эратосфена отпала бы.

Возрастающие и убывающие последовательности

Рассмотрим послед-ть, заданную формулой а_n = 5n:

Очевидно, что каждый следующий член больше предыдущего. Это значит, что мы имеем дело с возрастающей последовательностью.

Теперь изучим послед-ть, заданной рекурсивным способом:

Выглядеть он будет так:

Ясно, что каждый следующий член послед-ти меньше предыдущего. Такой ряд чисел называется убывающей последовательностью.

Убывающие и возрастающие послед-ти называют также монотонными последовательностями.

Для того, чтобы определить характер послед-ти, достаточно найти разность членов а_nи а_n+1. Если получается положительное выражение, то послед-ть возрастает, а если выражение отрицательно, то послед-ть убывает. Если получилось выражение, которое может иметь различный знак, то послед-ть вовсе не является монотонной.

Пример. Послед-ть задана формулой a_n = n/(n + 1). Является ли она убывающей либо возрастающей?

Решение. Запишем выражения для вычисления n-ого и (n+ 1)-ого члена послед-ти:

Осталось найти их разницу:

При натуральных значениях n полученная разница является положительным числом. Это значит, что каждый следующий член больше предыдущего, то есть послед-ть является возрастающей.

Пример. Исследуйте на монотонность послед-ть, заданную формулой

Решение. Если выписать первые члены послед-ти, может показаться, что она – убывающая:

Но это не так. Запишем выражения для n-ого и (n + 1)-ого члена послед-ти:

Теперь найдем их разность:

Получили выражение (2n– 7), которое может быть как отрицательным, так и положительным (при n≥ 4). Это значит, что послед-ть немонотонна. В этом можно убедиться, вычислив четвертый и пятый член послед-ти:

Получаем, что у₅>у₄, поэтому послед-ть не является убывающей

Ответ: послед-ть немонотонна.

Ограниченные и неограниченные последовательности

Изучим послед-ть, заданную с помощью формулы b_n = 1/n. Её первые члены будут выглядеть так:

Очевидно, что она является убывающей, ведь каждая следующая дробь меньше предыдущей. Вместе с тем все члены послед-ти являются положительными числами. Это значит, что для каждого n выполняется неравенство b_n> 0. То есть последовательность ограничена числом 0. В математике такие послед-ти называют ограниченными снизу.

Существует и послед-ти, ограниченные сверху. Это такие послед-ти, каждый член которых меньше какого-то постоянного числа.

В качестве примера можно привести послед-ть, заданную формулой с_n = 1 – 1/n. Каждый следующий ее член все ближе к единице, но ни один из них не достигает ее. Покажем, как строго доказать это. Для этого используют метод рассуждений «от противного».

Предположим, что послед-ть с_n = 1 – 1/n не ограничена числом 1 сверху. Тогда существует такой ее член с_n, для которого выполняется условие

Попытаемся найти номер этого члена:

Полученное нер-во выполняется только для отрицательных n. Но n – это натуральное, то есть положительное число. Это говорит о том, что не существует такого натурального n, для которого справедливо нер-во 0 ≥ 1/n. Значит, и не существует такого с_n, для которого верно нер-во с_n ≥ 1. Из этого следует, что послед-ть ограничена сверху числом 1.

Пример. Докажите, что послед-ть m_n = n 2 – 6n + 4 ограничена снизу числом (– 6).

Решение. Предположим, что на самом деле послед-ть не ограничена снизу числом (– 6). Тогда хотя бы для одного ее члена будет выполняться нер-во

Найдем номер этого члена:

Получили неравенство второй степени. Для его решения следует найти корни квадратного трехчлена. Начнем с вычисления дискриминанта:

Дискриминант отрицательный, а ветви параболы смотрят вверх. Поэтому схематично парабола относительно оси Ох будет располагаться так:

Видно, что нер-во решений не имеет. Значит, не существует такого номера n, для которого верно условие m_n ≤ – 6. Следовательно, послед-ть ограничена снизу числом (– 6).

Если послед-ть ограничена одновременно и снизу, и сверху, то ее называют просто ограниченной послед-тью.

Примером ограниченной последовательности является b_n = 1/n. С одной стороны, она ограничена нулем снизу. С другой стороны, она ограничена сверху числом 2, так как первый ее член равен единице, а вся послед-ть – убывающая.

Примером неограниченной последовательности является v_n = 5n, ведь ее невозможно ограничить сверху.

Примером ограниченной последовательности является b_n = 1/n. С одной стороны, она ограничена нулем снизу. С другой стороны, она ограничена сверху числом 2, так как первый ее член равен единице, а вся послед-ть – убывающая.

Примером неограниченной последовательности является v_n = 5n, ведь ее невозможно ограничить сверху.

Видно, что формула работает. Однако, сколько бы раз мы не проверяли ее, это не будет служить строгим доказательством ее справедливости. Возможно, что она будет работать для первого миллиона члена послед-ти, а для 1000001-ого даст ошибку. Поэтому поступим иначе. Предположим, что фор-ла S_n= n 2 верна хотя бы для одного значения n, равного k:

Докажем, что тогда она будет верна и для следующего числа k + 1. То есть нужно доказать равенство

Ясно, что сумму (k + 1) членов послед-ти можно получить, прибавив к сумме k членов (то есть к S_k )ещё одно слагаемое a_n+1, то есть справедлива запись:

При этом мы предположили, что верно равенство

а число a_n+1 можно посчитать по формуле n-ого члена:

Тогда можно записать

Получили формулу сокращенного умножения – квадрат суммы. Его можно «свернуть»:

Сформулируем принцип математической индукции:

То есть сначала надо доказать, что утверждение выполняется при n = 1. Это действие называют шагом индукции. Далее предполагают, что утверждение верно при n = k, и из этого выводят, что оно верно и для n =k + 1.

Пример. Докажите с помощью математической индукции, что сумма квадратов первых n натуральных чисел вычисляется по формуле:

Решение. Докажем базис индукции, то есть то, что утверждение верно при n = 1. Действительно, подставив единицу в формулу, получим:

Получили один и тот же результат. Базис индукции доказан.

Теперь предположим, что формула верна для произвольного n = k:

Тогда сумма (k + 1) квадратов может быть найдена по формуле

Подставим в нее выражение для S_k и получим:

С другой стороны, нам надо доказать, что величина S_k+1определяется по формуле

Приравняем выражения (1) и (2) и покажем, что они тождественно равны:

Умножим обе части на 6 и получим:

Получили одинаковые выражения в обоих частях рав-ва, поэтому оно является верным при любом значении k. Значит, мы смогли доказать шаг индукции, и следовательно, всё исходное утверждение.

Пример. Докажите, что любую сумму, большую 7 копеек, можно оплатить, используя только два типа монет: по 3 и 5 копеек.

Это утверждение, очевидно, верно сумм в 8, 9 и 10 копеек:

Добавив к этим суммам ещё одну трехкопеечную монету, мы сможем получить выражения для следующих трех чисел:

С помощью ещё одной монетки в три копейки можно уплатить следующие 3 суммы:

Ясно, что продолжая подобные рассуждения, можно для любого натурального числа записать эквивалентную ему сумму пятерок и троек, что доказывает утверждение из условия.

Последовательности в жизни

Порою, изучая математические объекты, люди задумываются – а какое отношение все эти формулы имеют к реальной жизни? Встречаются ли последовательности в природе и обществе, или они являются лишь плодом фантазии математиков?

На самом деле последовательности имеют большое практическое приложение. Так, Фибоначчи сформулировал свою последовательность тогда, когда изучал скорость размножения кроликов. Если каждая пара кроликов рожает в месяц ещё одну пару, а через месяц и старая, и новая пара рожает ещё кроликов, то их численность будет расти также, как и последовательность Фибоначчи! Аналогично протекают процессы роста популяций других животных.

Большое значение последовательности имеют в программировании. Дело в том, что порою программам нужно получить некоторое случайное число, чтобы имитировать случайные события. Однако по ряду причин компьютеру тяжело сгенерировать истинно случайное число, поэтому часто используют генераторы псевдослучайных чисел. Это особые алгоритмы, порождающие последовательности чисел, которые кажутся случайными, хотя таковыми на самом деле не являются.

Встречаются последовательности и в астрономии. В частности, расстояние от планет до Солнца примерно можно рассчитать с помощью особой последовательности Тициуса-Боде. Последние исследования показывают, что и расположение планет в других планетных системах хорошо описывается этой последовательностью.

Источник

Вопрос 2. Ограниченная последовательность.

Вопрос 1. Числовая последовательность. Примеры.

Числовая последовательность – функция натурального аргумента: f(n)=x_n

Определение: если по некоторому закону каждом натуральному числу n поставлено в соответствие вполне оптимальное число x_n, то говорят, что задана числовая последовательность < x_n >.

1) 2,4,6..2n,…(монотонная, неограниченная)

2) 1,0,1,0,…(немонотонная, ограниченная)

Вопрос 2. Ограниченная последовательность.

Послед. x_n называется ограниченной, если существуют два числа m,M такие, что x_n находится в пределах m≤ x_n≤M.

-Последовательность называется ограниченной, если она одновременно ограничена и сверху и снизу.

Вопрос 3. Предел числовой последовательности.

Определение: число А называется пределом последовательности < а_n >, если для любого положительного числа ε>0 найдется такой N(номер, зависящий от ε), начиная с которого будет выполняться неравенство: |х _n-а| N имеем

,

И, поскольку ε является как угодно малым положительным числом, как единственно возможное, имеем

Вопрос 5. Ограниченность сходящейся последовательности.

Если последовательность имеет конечный предел, то последовательность ограничена.

Если последовательность сходится, то она ограничена.

Доказательство: пусть последовательность сходится, то есть . Тогда по определению выполняется . Пусть =1, тогда .

Пусть M=max < >

m=min < >, тогда .

Значит, по определению последовательность является ограниченной.

Ограниченность последовательности является необходимым условием сходимости, но не является достаточным. Существуют ограниченные последовательности, которые не являются сходящимися.

Например, .

Пусть последовательность ограничена, будет ли она сходящейся? – Ограниченная сходимость следует не всегда.

неограниченная

ограниченная

Вопрос 6. Свойства пределов, связанные с арифметическими действиями (для последовательности)

4)

Вопрос 7. Переход к пределу в неравенствах

Пусть и ; ,

Тогда

Вопрос 30. Теорема Ролля

Пусть функция f(x) дифференцируема внутри интервала (a;b)- непрерывна на сегменте и на f(a)=f(b) (на концах отрезка принимает равные значения)найдется такая точка, в которой производная равна 0.

Геометрический смысл теоремы: Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс; в этой точке производная и будет равняться 0.

Проиллюстрируем эту теорему геометрически:

Найдет такая точка С, в которой касательная будет горизонтальна в этой точке производная равна 0.

Доказательство: Пусть функция f(x) – постоянна х ∈ (a;b), тогда значение производной во всех точках равно 0.

f(x)- не является константой.

Пусть f(x)>f(a), значение на концах функции равны

Пусть f(x)>f(a), по условию f(a)=f(b)=>f(x)>f(b)

Теорема Коши.

Пусть f(x) и g(x) непрерывны на отрезке [a;b] и дифференцируема на интервале (a;b), тогда справедлива следующая формула:

, где — какая-то точка из интервала (a;b)

Экстремум функции

— в точке х₀ у функции будет max, если в окрестности точки х₀ f(x₀)>f(x)

Тогда функция в точке х=х₀ не может не возрастать, не убывать.

—Достаточное условие экстремума.

Вопрос 47. Таблица интегралов.

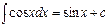Таблица интегралов проверяется дифференцированием.

Вопрос 60.Числовые ряды

Числовым рядом называется сумма , a_n— общий член ряда.

Признак Коши.

Пусть существует предел , тогда:

1)q 1-ряд расходится

3)q=1- ничего сказать нельзя(признак не работает)

Доказательство:

Для любого положения числа ε(∀ε>0) мы имеем

— это геометрическая прогрессия со знаком сходится, поэтому по признаку сравнения исходный ряд сходится.

За счет выбора ε можно q-ε>1

Признак Даламбера.

Пусть существует , тогда

1)q 1-ряд расходится

3) q=1- нужны дополнительные сведения.

— сходится => исходный ряд тоже сходится.

2) q>1 аналогично, как признак Коши.

Признак Лейбница

Если члены знакочередующегося ряда убывают по абсолютной величине u₁>u₂>u₃>…>u_n>… и предел его общего члена при n→∞ равен 0, т.е. , то ряд сходится, а его сумма не превосходит первого члена: S≤u₁.

и 2b_n 4b_n ↓0

1) строгое знакочередование

b_n→0 n→∞

2) Рассмотрим ряд из модулей

— расходится, поэтому сходимость у исходного ряда условная.

Вопрос 1. Числовая последовательность. Примеры.

Числовая последовательность – функция натурального аргумента: f(n)=x_n

Определение: если по некоторому закону каждом натуральному числу n поставлено в соответствие вполне оптимальное число x_n, то говорят, что задана числовая последовательность < x_n >.

1) 2,4,6..2n,…(монотонная, неограниченная)

2) 1,0,1,0,…(немонотонная, ограниченная)

Вопрос 2. Ограниченная последовательность.

Послед. x_n называется ограниченной, если существуют два числа m,M такие, что x_n находится в пределах m≤ x_n≤M.

-Последовательность называется ограниченной, если она одновременно ограничена и сверху и снизу.

Источник