Что значит ограниченная функция сверху
Что значит ограниченная функция сверху
Функция y=f(x), определенная на множестве X, называется ограниченной сверху, если множество её значений ограниченно сверху. Иначе говоря, функция f(x) ограничена сверху, если существует такая постоянная М, что для каждого \(x \in X\) выполняется неравенство \(f(x) \leqslant M.\)
· Функция y=f(x), определенная на множестве Х, называется ограниченной снизу, если множество её значений ограниченно снизу, то есть если существует такая постоянная М, что для каждого \(x \in X\) выполняется неравенство \(f(x) \leqslant M.\)
· Функция f(x), определенная на множестве Х, называется ограниченной, если множество её значений ограниченно как сверху, так и снизу.
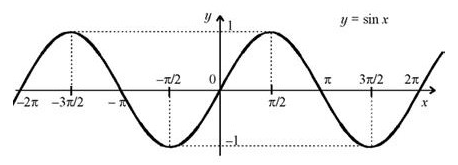
Примерами функций, ограниченных на всей числовой прямой, являются функции y=sin x, y=cos x.
При решении уравнений и неравенств свойство ограниченности функций часто играет определяющую роль. Например:
Рассмотрим пример применения данных выводов.
Решение: Функции, записанные в левой и правой частях уравнения, определены при всех действительных значениях х. Кроме того, для любых х верно:
Следовательно, данное уравнение равносильно системе уравнений:
Решения второго уравнения системы есть х=0 и х=-1. Из этих значений первому уравнению удовлетворяет только х=0, которое, следовательно, является единственным решением исходного уравнения.