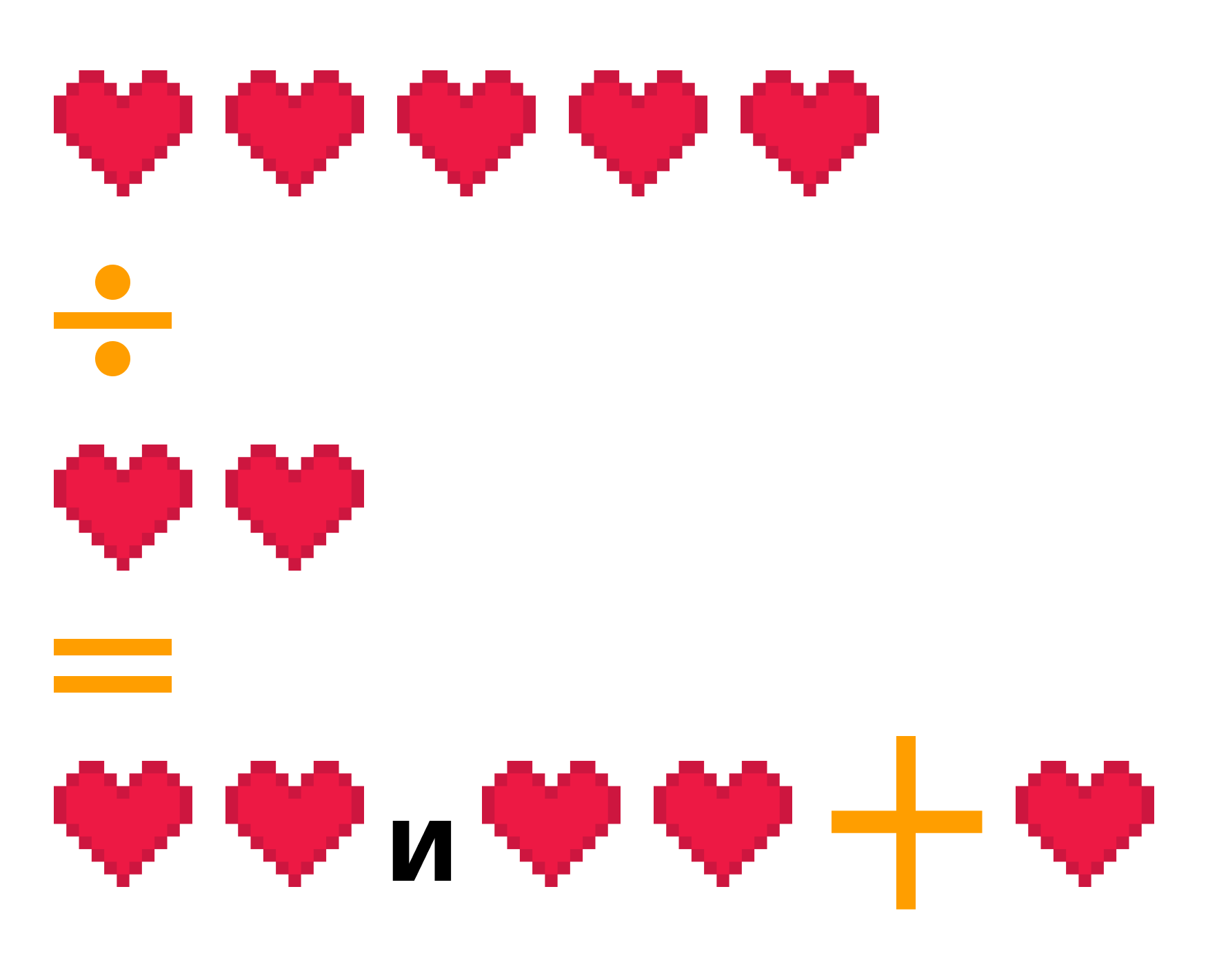Что значит одинаковая четность
Применение свойств четности и нечетности чисел при решении тестовых задач в 5-6 классах средней школы
Введение. Понятие чётности очень важно для развития математической культуры школьника. Теоретически это понятие простое и обычно не вызывает трудностей. Задачи же, связанные с чётностью, могут варьироваться от самых простых до очень сложных. Эти задачи позволяют на простом материале ввести школьника в разнообразный круг математических идей.
Вводная задача 1. Николай с сыном и Пётр с сыном пошли на рыбалку. Николай поймал столько же рыб, сколько его сын, а Пётр — столько же, сколько его сын. Все вместе поймали 27 рыб. Сколько рыб поймал Николай?
Решение. Сначала кажется, что в задаче не хватает данных: два неизвестных и одно уравнение. Затем кто-то должен сообразить, что условия задачи противоречивы. Действительно, отцы поймали столько же рыб, сколько и сыновья. Но тогда общее число рыб должно быть чётным, а по условию оно нечётно.
Вариант рассуждения: Николай с сыном вместе поймали чётное число рыб. То же верно и для Петра с сыном. Значит, и сумма этих чисел чётна. (Если школьники сами не догадаются до одного из этих соображений, следует им немного подсказать).
Но никакого противоречия нет! К противоречию привело неявное предположение о том, что на рыбалке было четыре человека. Но их могло быть и три (Николай — сын или отец Петра). Из условия теперь следует, что все поймали рыб поровну, то есть по 9 штук. С этой задачей (но не с её решением) желательно ознакомить школьников за несколько дней до начала первого занятия. [1]
1. Определение четных и нечетных чисел
Понятие четности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечетные числа соответствовали ян, что означало небо, благоприятность, а четные – это инь, земля, изменчивость, неблагоприятность. В Европе и некоторых восточных странах считается, что четное количество даримых цветов приносит счастье. В России четное количество цветов принято приносить лишь на похороны умершим. В случаях, когда в букете много цветов, четность или нечетность их количества уже не играет такой роли.
Далее идет обсуждение вводной задачи. Она позволяет начать разговор об определении и свойствах чётности. Прежде всего, мы использовали тот факт, что число вида п + п чётно (отцы поймали столько же рыб, сколько сыновья, поэтому вместе они поймали чётное число рыб).
Вот ещё одна задача, иллюстрирующая ту же идею.
Задача 2. Кузнечик прыгал вдоль прямой и вернулся в исходную точку. Все прыжки имеют одинаковую длину. Докажите, что он сделал чётное число прыжков.
Решение. Сколько раз он прыгнул вправо, столько же прыгнул и влево (так как вернулся в исходную точку)… Откуда следует, что число вида п + п = 2п чётно? А это просто определение.
Определение. Целое число называется четным, если оно делится на 2 без остатка, и нечетным, если оно на 2 не делится.
Таким образом, «общий вид» чётного числа 2п, где п — произвольное целое число. Речь идёт именно о целых, а не только о натуральных (то есть целых положительных) числах. В частности, важно понимать, что 0 — тоже чётное число.
Каков же «общий вид» нечётного числа? 2n + 1. Действительно, если от нечётного числа отнять 1, то оно станет чётным, то есть нечётное число равно сумме чётного числа 2п и единицы. Часто используется запись нечётного числа и в виде 2п — 1.
2. Свойства четных и нечетных чисел
Свойство 1. Из определения чётного числа сразу следует, что произведение любого (целого) числа на чётное число чётно. Доказательство: k • 2п = 2(kn).
Свойство 2. Несколько более сложно проверить, что произведение двух нечётных чисел нечётно. Доказательство: (2k + l)(2n + 1) = 2(2kп + k + п) + 1.
Определение. Два целых числа называются числами одинаковой четности, если оба четные или оба нечетные. Два целых числа называют числами разной четности, если одно из них четное, а другое нечетное.
Свойство 3. Сумма двух чисел разной чётности нечётна.
Доказательство: 2k + 2п + 1 = 2(k + п) + 1 = 2m + 1, где m = k + п – целое число. Сумма нечетна.
Свойство 4. Сумма двух чисел одной чётности чётна.
Доказательство: 2k + 2п = 2(k + п) = 2m, где m = k + п — целое число. Таким образом, сумма — четное число.
2k + 1 + 2п + 1 = 2(k + п + 1) = 2m, где m = k + п + 1 — целое число. Таким образом, сумма — четное число.
Обратные утверждения. Затем можно предложить ребятам сформулировать и доказать утверждения, обратные утверждениям о четности суммы.
Если сумма двух чисел нечётна, то слагаемые имеют разную чётность. Доказательство. Действительно, если бы они имели одинаковую чётность, то сумма была бы чётной.
Если сумма двух чисел чётна, то слагаемые имеют одинаковую чётность. Доказательство аналогично.
Перейдем к следующему свойству четных и нечетных чисел.
Задача 3 (подготовительная). Сумма трех чисел нечётна. Сколько слагаемых нечётно? Ответ: одно или три.
Решение. Нетрудно привести примеры, показывающие, что оба случая возможны. Остальные два случая (нечётных слагаемых два или их нет совсем) легко приводятся к противоречию. Теперь можно перейти к наиболее общей формулировке.
Свойство 5. Чётность суммы совпадает с чётностью количества нечётных слагаемых.
Аналогичные рассуждения приводятся для нечетного количества нечетных слагаемых. Учащиеся делают вывод: нечетность суммы совпадает с нечетностью количества нечетных слагаемых.
3. Задачи на применение свойств четности и нечетности [2]
Задача 4. Хозяйка купила общую тетрадь объемом 96 листов и пронумеровала все ее страницы по порядку числами от 1 до 192. Щенок Антошка выгрыз из этой тетради 25 листов и сложил все 50 чисел, которые на них написаны. Могло ли у него получиться 1990?
Решение. На каждом листе сумма номеров страниц нечетна, а сумма 25 нечетных чисел – нечетна. Поэтому число 1990 у Антошки получиться не могло.
Задача 5. В школе 1688 учащихся, причем мальчиков на 373 больше, чем девочек. Доказать, что такого не может быть.
Решение. Если девочек х, то всего учеников 2х + 373, а это число нечетное как сумма четного и нечетного чисел.
Задача 6. Четно или нечетно число 1 – 2 + 3 – 4 + 5 – 6 + … + 993?
Задача 7. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки плюс и минус, чтобы получилось выражение, равное нулю?
Задача 8. Можно ли разменять 100 рублей при помощи 25 монет достоинством 1 и 5 рублей?
Задача 9. В пятиэтажном доме с четырьмя подъездами подсчитали число жителей на каждом этаже и, кроме того, в каждом подъезде. Могут ли все полученные 9 чисел быть нечетными?
Решение. Обозначим число жителей на этажах соответственно через a1, a2, a3, a4, a5, a число жителей в подъездах соответственно через b1, b2, b3, b4. Тогда общее число жителей дома можно подсчитать двумя способами — по этажам и по подъездам:
a1 + a2 + a3 + a4 + a5 = b1 + b2 + b3 + b4. Если бы все эти 9 чисел были нечетными, то сумма в левой части записанного равенства была бы нечетной, а сумма в правой части — четной. Следовательно, это невозможно.
Задача 10. Верно ли равенство 1 2 + 2 3 + 3 4 + … + 99 100 = 20002007?
Решение. Произведения четного и нечетного чисел четны, а сумма четных слагаемых всегда четна.
Задача 11. Четна или нечетна сумма всех натуральных чисел от 1 до 17?
Задача 12. Кузнечик прыгает по прямой: первый раз на 1 см, второй раз на 2 см и т.д. Может ли он через 25 прыжков вернуться на прежнее место?
Решение. Чтобы вернуться на старое место, общее количество сантиметров должно быть четно, а сумма 1 + 2 + 3 + … + 25 нечетна. Поэтому вернуться на прежнее место кузнечик не сможет.
Задачи для самостоятельного решения
Задача 13. Можно ли разменять 25 рублей десятью монетами достоинством 1, 3 и 5 руб.?
Решение. Если мы сложим четное число каких-либо целых чисел, то получим число четное, а 25 — нечетное число. Поэтому разменять 25 руб. таким образом нельзя.
Задача 14. В магазин «Все для собак и кошек» привезли новые игрушки. Могут ли десять игрушек ценой в 3, 5 или 7 рублей стоить в сумме 53 рубля?
Решение. Сумма четного количества нечетных чисел четна. У нас есть 10 чисел (цена одной игрушки), все они нечетные, значит, их сумма должна быть четна. Но 53 – число нечетное, поэтому получить его в виде суммы 10 нечетных чисел нельзя.
Задача 15. У Антона было 5 плиток шоколада. Может ли Антон, поделив каждую плитку на 9, 15 или 25 кусочков, получить всего 100 кусков шоколада?
Решение. Нет, т.к. если сложить 5 нечетных чисел, получим нечетный результат. А число 100 четно.
Задача 16. У Нины было 11 плиток шоколада фабрики «Краскон». Может ли Нина, поделив каждую плитку на 7, 13 или 21 кусочков, получить всего 100 кусков шоколада?
Решение. В выражении нечетное количество нечетных чисел. Ответ должен быть нечетным числом.
4. Задачи на чередование [2]
Свойства чередования:
Задача 18. Может ли вращаться система из 7 шестеренок, если первая сцеплена со второй, вторая с третьей и т.д., а седьмая сцеплена с первой?
Решение. Нет. Если первая вращается по часовой стрелке, то все нечетные шестеренки должны вращаться по часовой стрелке, а первая и седьмая одновременно вращаться по часовой стрелке не могут.
Задача 19. Может ли конь пройти с поля a1 на поле h8, побывав по дороге на каждом из остальных полей ровно один раз?
Решение. Нет, не может. Так как конь должен сделать 63 хода, то последним (нечетным) ходом он встанет на поле другой четности, нежели a1; но h8 имеет тот же цвет.
Задача 20. Все костяшки домино выложили (соблюдая правила игры) в одну длинную цепь. На одном конце этой цепи оказалось 5 очков. Сколько очков может быть на другом конце цепи?
Решение. Если где-то лежит костяшка ∗ − 5, то рядом с ней лежит костяшка 5 − ∗ — возникает разбиение на пары. Сколько костяшек с пятеркой всего? Все ли они в этом разбиении на пары участвуют?
Задачи на разбиение на пары [2]
Свойство: если предметы можно разбить на пары, то их количество четно.
Решение. Если бы такое было возможно, то все звенья ломаной разбились бы на пары пересекающихся. Однако тогда число звеньев должно быть четным.
Задача 22. Семь тринадцатируков с планеты Тринадцатирук решили устроить турнир по армреслингу. Смогут ли они одновременно провести поединки для всех своих рук, чтобы все руки принимали участие, и в каждом поединке встречалось ровно две руки?
Решение. Тринадцатируки не смогут провести поединки для всех рук одновременно, так как в каждом поединке принимает участие две руки, а всего рук 13 · 7 = 91.
Задача 23. В народной дружине 100 человек и каждый вечер трое из них идут на дежурство. Может ли через некоторое время оказаться так, что каждый с каждым дежурил ровно один раз?
Решение. Так как на каждом дежурстве, в котором участвует данный человек, он дежурит с двумя другими, то всех остальных можно разбить на пары. Однако 99 – нечетное число.
1. Медников Л. Э. Четность. – 4-е изд., стереотип. – М.: МЦНМО, 2013.
2. Генкин С. А., Итенберг И. В., Фомин Д. В. Ленинградские математические кружки: пособие для внеклассной работы. Киров, издательство «АСА», 1994.
Четные и нечетные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Четные и нечетные числа: что, как, зачем, почему
Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.
Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.
Четное число — это число, которое делится на 2.
4 : 2 = 2
Это значит, что 4 — четное число.
Нечетное число — это число, которое не делится на 2.
5 не делится на 2 без остатка — значит, 5 это нечетное число.
Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.
Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.
Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.
Свойства четных и нечетных чисел
Четные и нечетные числа чередуются друг с другом
1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.
Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.
| 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 |
| 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 |
| 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| 4 | 14 | 24 | 34 | 44 | 54 | 64 | 74 | 84 | 94 |
| 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
| 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 | 86 | 96 |
| 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 |
| 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 | 88 | 98 |
| 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.
Онлайн-курсы по математике для детей помогут быстрее освоить новую тему при поддержке опытного преподавателя.
Задачи для практики
Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.
Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?
| 1 | ♥ | 17 |
| 2 | 10 | ♥ |
| ♥ | 11 | 19 |
| 4 | ♥ | 20 |
| 5 | 13 | ♥ |
| ♥ | 14 | 22 |
| 7 | 15 | 23 |
| 8 | ♥ | ♥ |
Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.
Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | |||||
| X : 2 |
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | 4 | 8 | 12 | 16 | 20 |
| X : 2 | 1 | 2 | 3 | 4 | 5 |
2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
10 : 2 = 5 — нечетное
Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
15 + 12 = 27 (к)
Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.
Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?
Ответ: изначально у Маши в инстаграме было 46 фотографий.
Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.
| 1 | ☆ | 3 | ☆ | 5 |
| 6 | ☆ | ☆ | 9 | 10 |
| ☆ | 12 | 13 | ☆ | 15 |
| 16 | ☆ | ☆ | 19 | 20 |
| ☆ | 22 | 23 | ☆ | 25 |
Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.
Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70
Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
126 : 2 = 63
Что значит одинаковая четность
Четность и нечетность чисел
Сумма любого числа четных чисел – четно.
Сумма нечетного числа нечетных чисел – нечетно.
Сумма четного числа нечетных чисел – четно.
Идея четности имеет много разных применений. Самые простые из них:
1. Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).
2. Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов, если начало и конец одного вида, то нечетное число. (четное число объектов соответствует нечетному числу переходов между ними и наоборот . )
3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.
3′. Обратно: по числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли начальное состояние с конечным. (переформулировка п.3)
4. Если предметы можно разбить на пары, то их количество четно.
5. Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой предмет может быть не один (но их всегда нечетное число).
(!) Все эти соображения можно на олимпиаде вставлять в текст решения задачи, как очевидные утверждения.
Решение: Нет, не могут. Если бы они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки (для решения задачи не имеет никакого значения, в каком именно направлении вращается первая шестеренка !) Тогда всего должно быть четное число шестеренок, а их 9 штук?! ч.и.т.д. (знак «?!» обозначает получение противоречия)