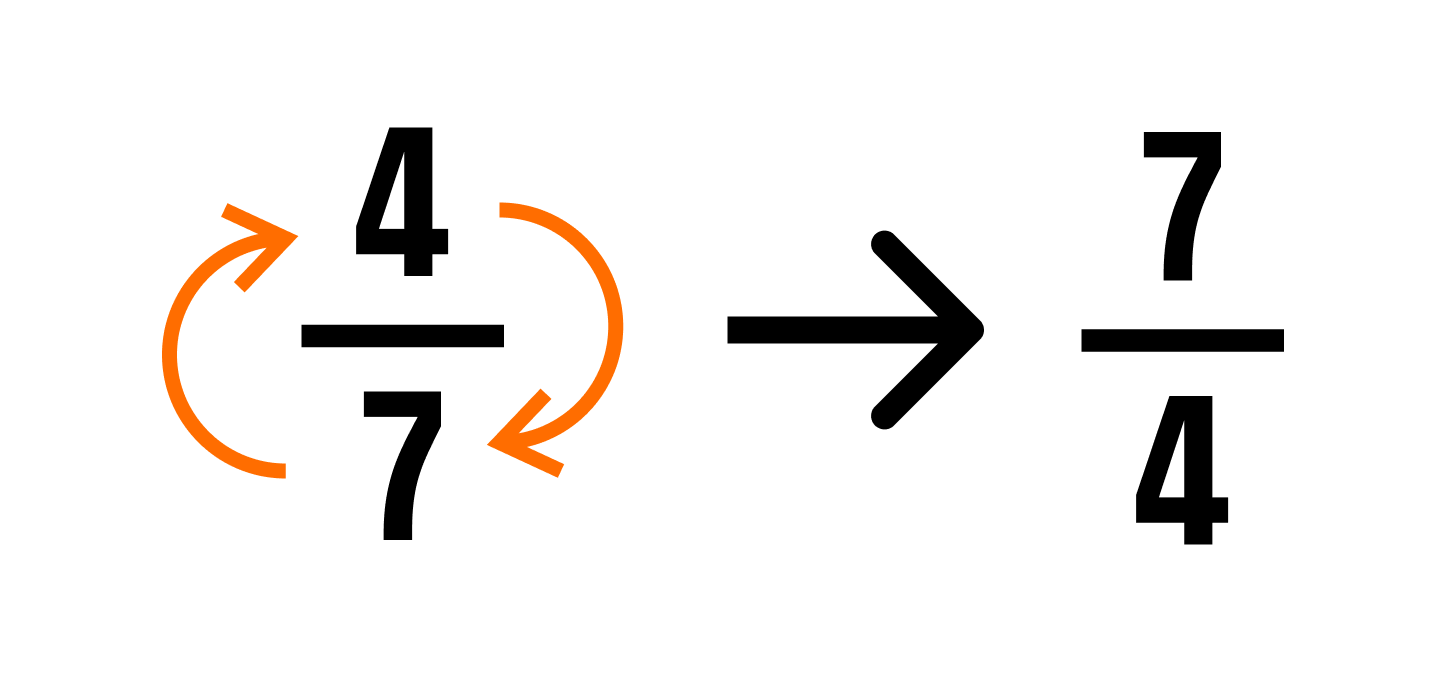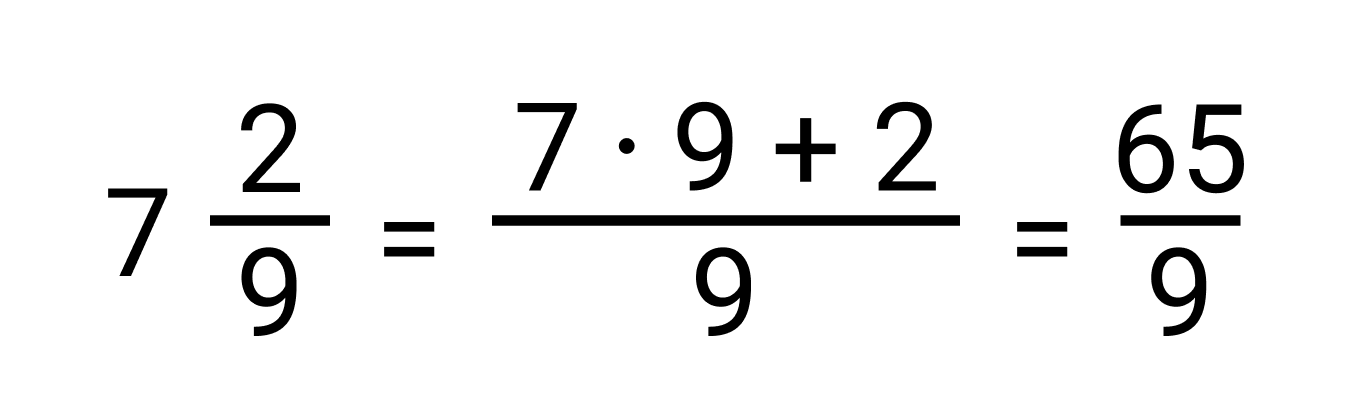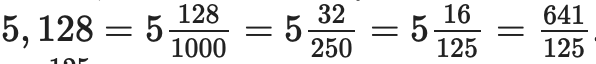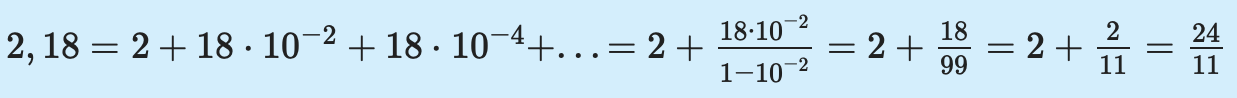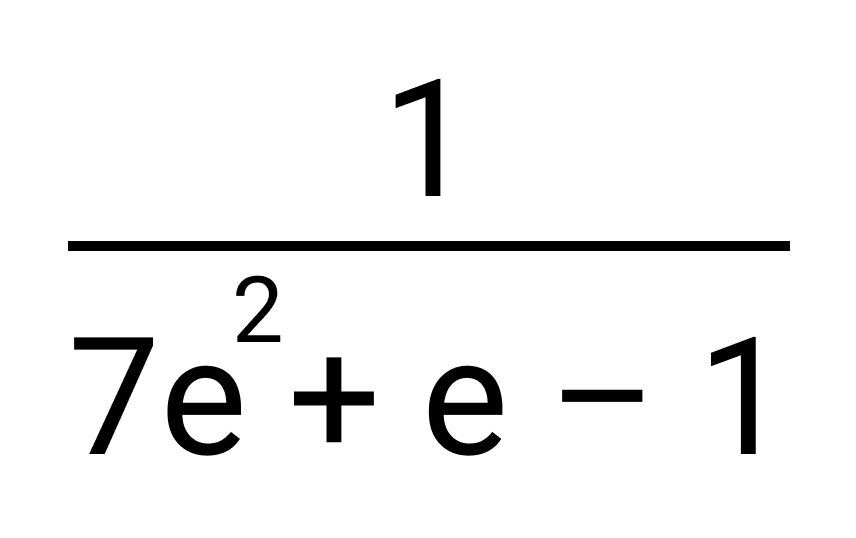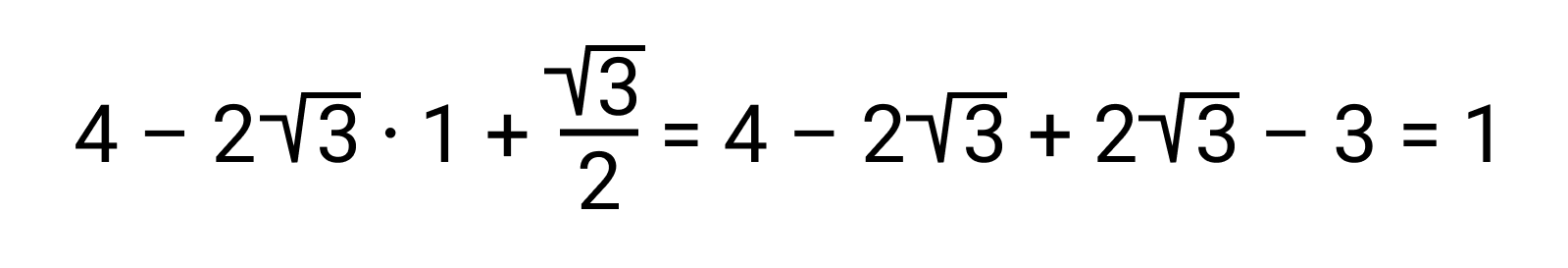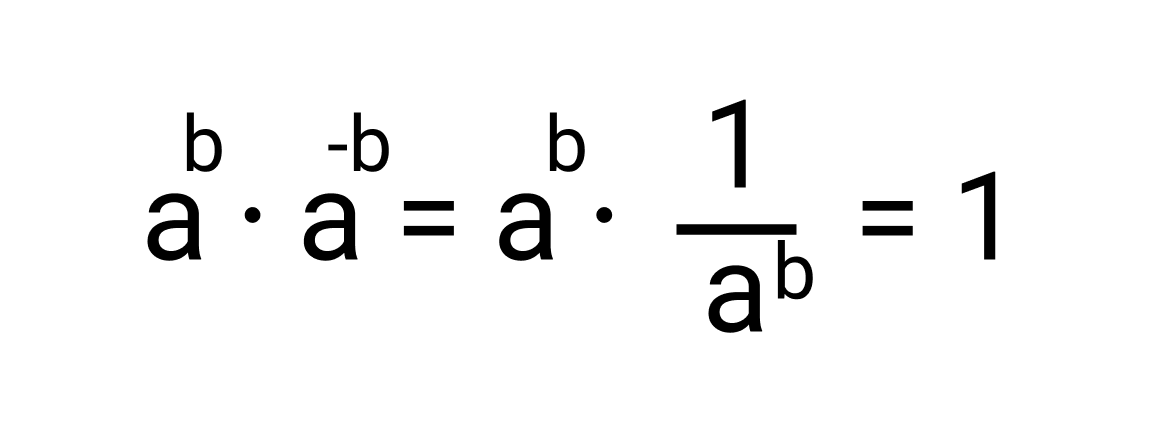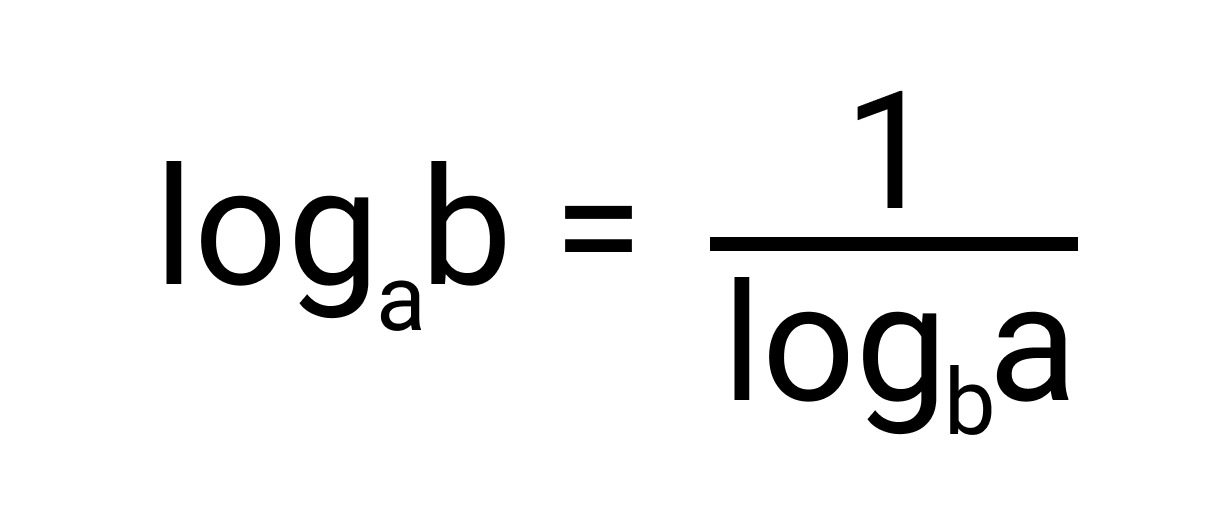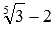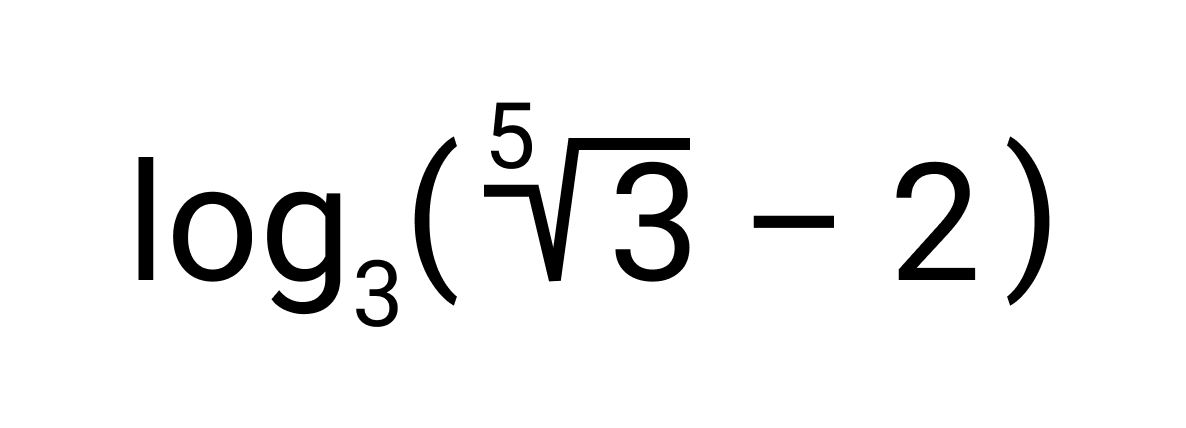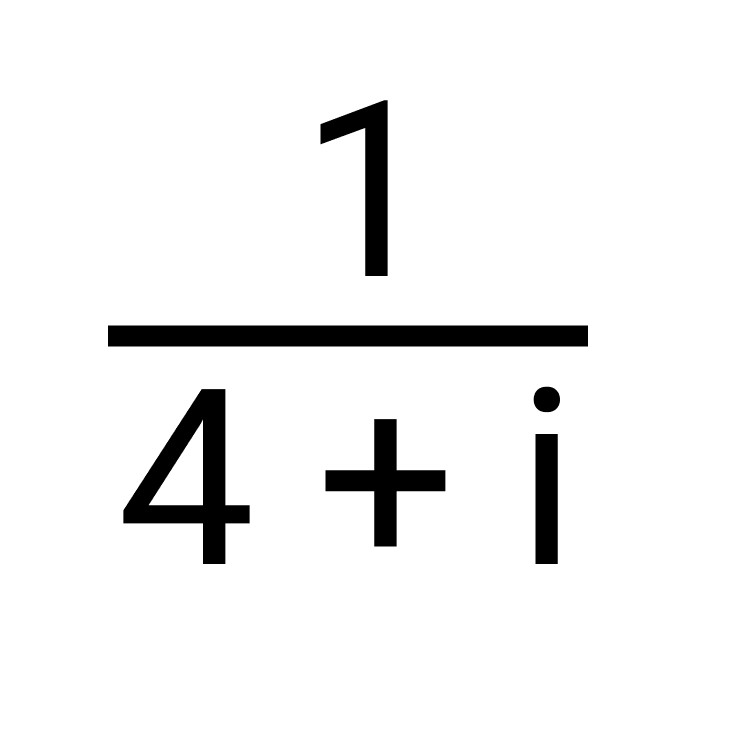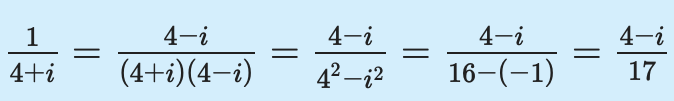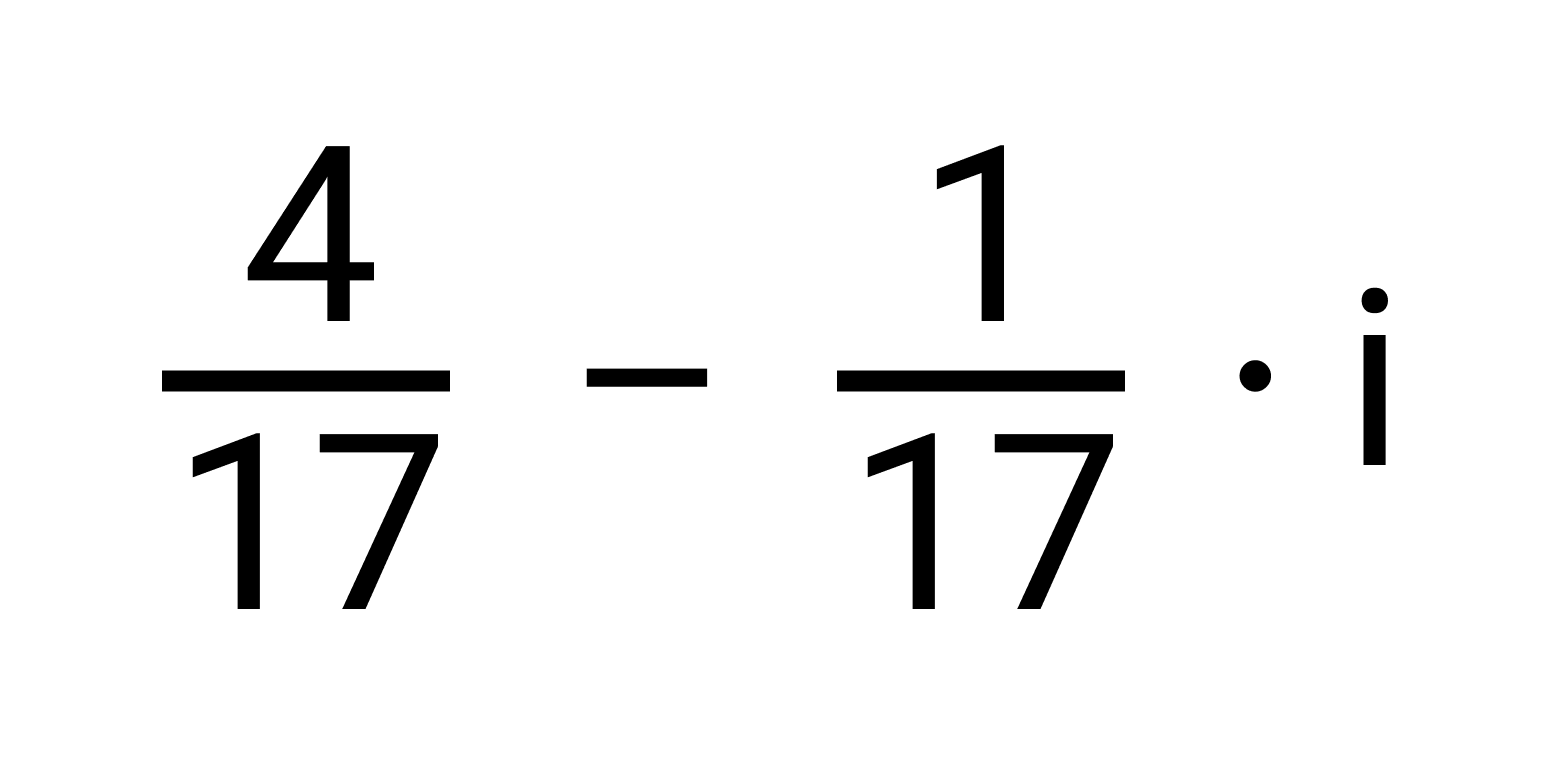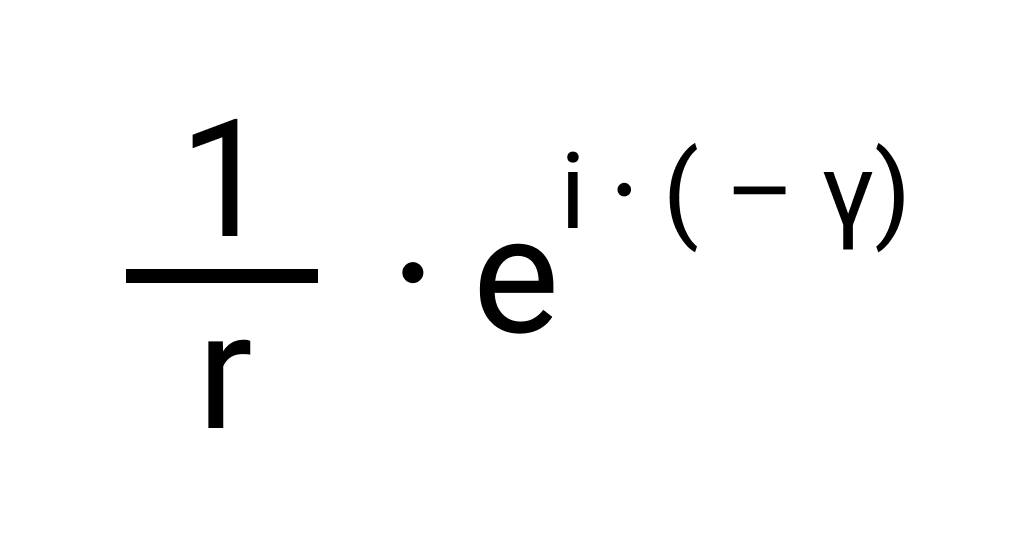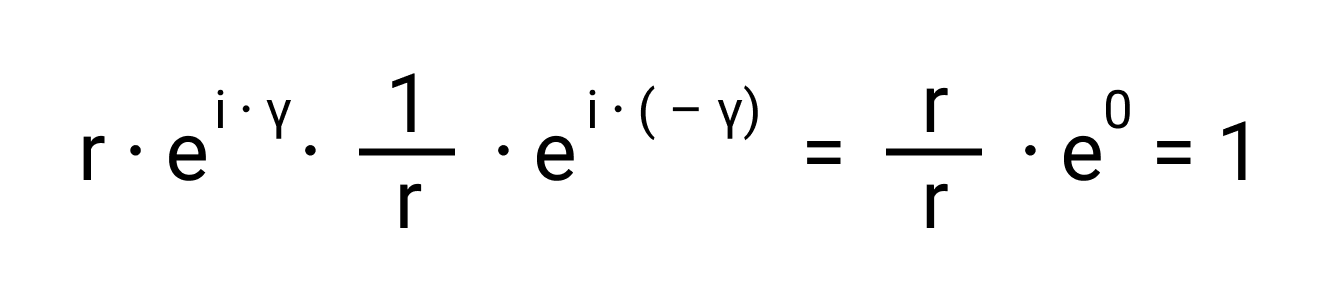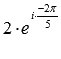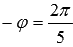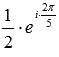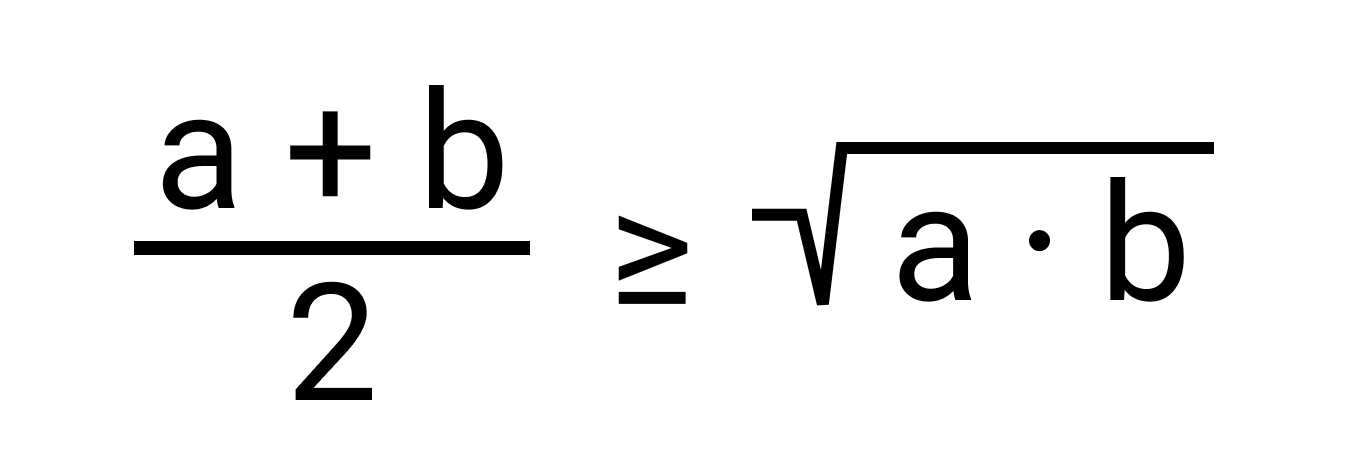Что значит обратное значение числа

Обратное число

Обра́тное число́ (обратное значение, обратная величина) — это число, на которое надо умножить данное число, чтобы получить единицу. Пара чисел, произведение которых равно единице, называются взаимно обратными.

Примеры: 5 и 1/5, −6/7 и −7/6, и

Для всякого числа а, не равного нулю, существует обратное 1/a.

Обратной величиной нуля является бесконечность.

Обратные дроби — это две дроби, произведение которых равно 1. Например, 3/7 и 7/3; 5/8 и 8/5 и т. д.

См. также

Полезное

Смотреть что такое «Обратное число» в других словарях:

ОБРАТНОЕ ЧИСЛО — число, произведение которого на данное число равно единице. Два таких числа называются взаимно обратными. Таковы, напр., 5 и 1/5, 2/3 и 3/2 и т. д … Большой Энциклопедический словарь

обратное число — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN inverse numberreciprocal number … Справочник технического переводчика

обратное число — число, произведение которого на данное число равно единице. Два таких числа называются взаимно обратными. Таковы, например, 5 и 1/5, 2/3 и 3/2 и т. д. * * * ОБРАТНОЕ ЧИСЛО ОБРАТНОЕ ЧИСЛО, число, произведение которого на данное число равно… … Энциклопедический словарь

Обратное число — число, произведение которого с данным числом равно единице. Два таких числа называются взаимно обратными. Таковы, например, 5 и а, не равного нулю, существует обратное … Большая советская энциклопедия

ОБРАТНОЕ ЧИСЛО — число, произведение к рого на данное число равно единице. Два таких числа наз. взаимно обратными. Таковы, напр., 5 и 1/5. 2/3 и 3/2 и т. д … Естествознание. Энциклопедический словарь

Число — У этого термина существуют и другие значения, см. Число (значения). Число основное понятие математики[1], используемое для количественной характеристики, сравнения и нумерации объектов. Возникнув ещё в первобытном обществе из потребностей… … Википедия

Число (матем.) — см. также: Число (лингвистика) Число абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое … Википедия

Обратное закручивание воды при стоке — Обратное закручивание воды при стоке околонаучный миф, основанный на неверном применении эффекта Кориолиса к движению воды в водовороте, возникающему при её стоке в сливное отверстие раковины или ванны. Суть мифа состоит в том, что вода… … Википедия

ЧИСЛО ИРРАЦИОНАЛЬНОЕ — ЧИСЛО, ИРРАЦИОНАЛЬНОЕ, число, которое не может быть выражено в виде дроби. Примеры включают Ц2 и число p. Следовательно, иррациональные числа это числа с бесконечным числом (непериодических) знаков после запятой. (Однако обратное не является… … Научно-технический энциклопедический словарь

Обратное преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия

Источник

Обратные Числа

и «перевернём» её, поменяв местами числитель и знаменатель.
Получим дробь.

называют обратной дроби.

опять «перевернуть», мы получим исходную дробь.

Поэтому такие дроби как

называют взаимно обратными.

Чтобы найти число обратное смешанному числу нужно:

записать его в виде неправильной дроби;

полученную дробь «перевернуть».

Пример. Найти число обратное смешанному числу:

Переворачиваем полученную дробь. Обратным числом для смешанного числа будет обыкновенная дробь:

Взаимно обратные числа обладают важным свойством.

Произведение взаимно обратных чисел равно единице.

Пример произведения обратных дробей.

Опираясь на свойство обратных дробей, можно дать определение взаимно обратных чисел.

Взаимно обратными числами называют два числа, произведение которых равно единице.

И так мы помним правило

Обратные числа (взаимно-обратные числа) — это два числа, произведение которых равно единице.

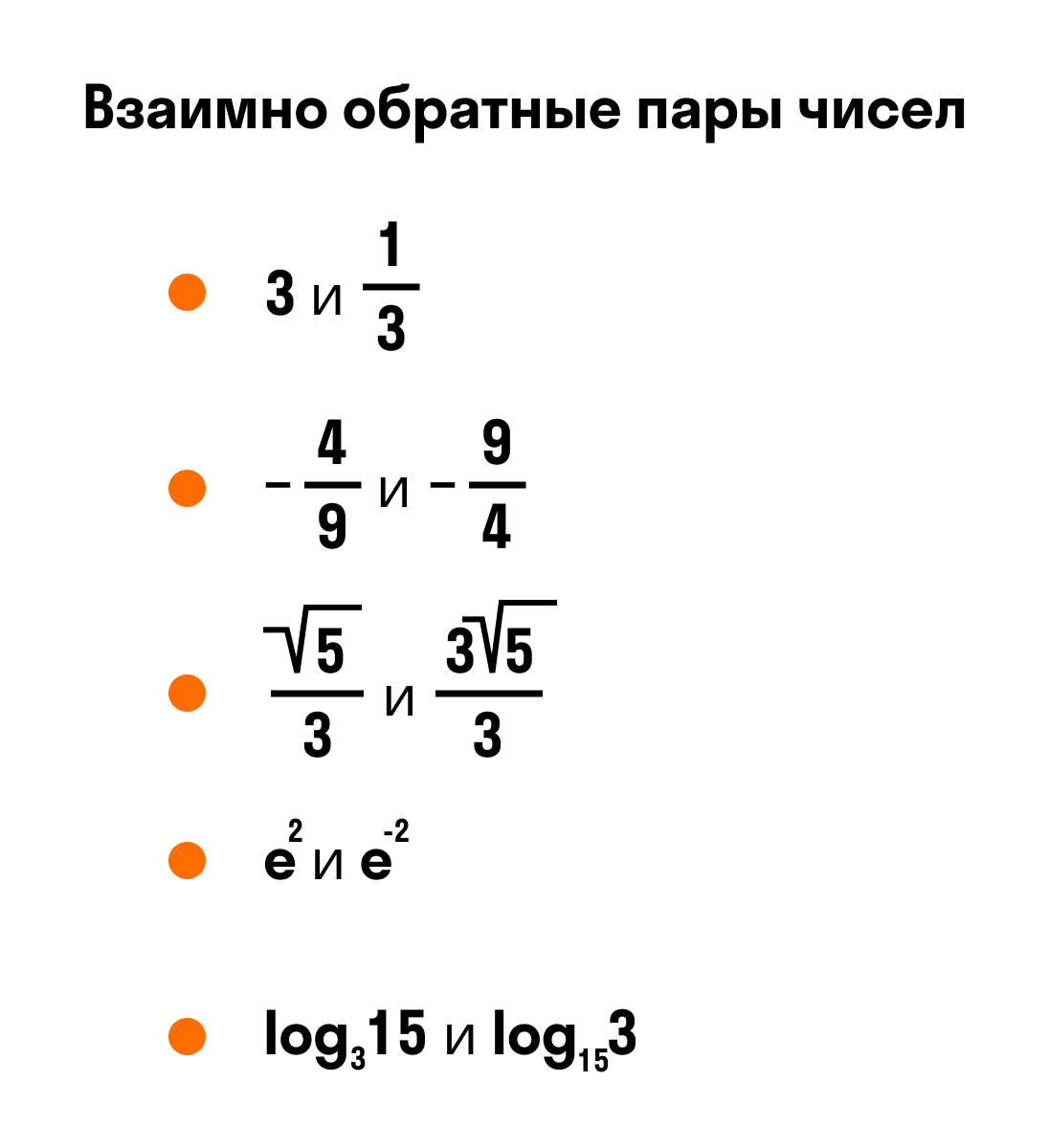
Примеры обратных чисел.

Обратное число существует для любого числа, кроме нуля.

Число, обратное 1 — это 1. Таким образом, единица — число, являющееся обратным самому себе.

В общем виде взаимно-обратные дроби можно представить как

натуральное число a и обратное ему число — как

Чтобы проверить, являются ли два числа обратными, надо найти их произведение. Если произведение равно единице, числа — взаимно-обратные, в противном случае числа обратными не являются.

Чтобы найти число, обратное данному, можно единицу разделить на данное число.

На практике обычно поступают проще.

Чтобы найти дробь, обратную обыкновенной дроби, числитель и знаменатель данной дроби меняют местами (дробь «переворачивают»).

Число, обратное натуральному, записывают как дробь с числителем 1 и знаменателем, равным данному натуральному числу.

Смешанные и десятичные дроби сначала переводят в обыкновенные дроби, а затем «переворачивают» и, если нужно, выделяют целую часть.

В алгебре по аналогии с взаимно-обратными числами вводится понятие взаимно-обратных выражений, в частности, обратных дробей.

Надеемся мы вам помогли, оставь отзыв и расскажи как ты понял( а) эту тему.

Источник

Взаимно обратные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение взаимно обратных чисел

С предыдущих уроков математики мы знаем: если прибавить или вычесть из числа нуль — оно не изменится. Точно также, если умножить или разделить число на единицу.

Ноль — нейтральный элемент для сложения и вычитания. При этом числа, которые в сумме дают ноль, называют противоположными.

Единица — нейтральный элемент для умножения и деления. Поэтому симметричными называют числа, чье произведение дает единицу.

Два числа называют взаимно обратными, если их произведение равно 1.

Обратное число к данному числу — это такое число, которое мы умножаем на данное число и получаем единицу.

Если числа a и b взаимно обратные, то можно сказать, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Также можно говорить, что числу a обратно число b, а числу b обратно число a.

Приведем примеры взаимно обратных чисел. Так как произведение двух единиц равно 1, то по определению числа 1 и 1 — взаимно обратные.

Определение взаимно обратных чисел относится к любым числам — натуральным, целым, действительным, комплексным.

Как найти число, обратное данному числу

Иногда число, обратное данному числу, очевидно. Так бывает с натуральными числами и обыкновенными дробями. В других случаях приходится проводить вычисления. Например, с иррациональными и комплексными числами.

Рассмотрим каждый отдельный случай нахождения числа, обратного данному числу.

Число, обратное обыкновенной дроби

Числом, обратным обыкновенной дроби a/b, является дробь b/a.

Чтобы это проверить, выполним умножение обыкновенных дробей a/b и b/a — получим 1. Значит дроби a/b и b/a — взаимно обратные числа.

Если числитель и знаменатель дроби a/b поменять местами, то получится дробь b/a, обратная дроби a/b.

Это правило значительно экономит время. Можно сразу записать число, обратное данной обыкновенной дроби без каких-либо вычислений.

Число, обратное натуральному числу

Нахождение числа, обратного данному натуральному числу, можно свести к нахождению числа, обратного дроби. Для этого нужно записать натуральное число как дробь со знаменателем 1.

Пусть нам дано натуральное число n, и нужно записать число, обратное числу n. Так как натуральное число n равно дроби n/1, то, поменяв местами числитель и знаменатель этой дроби, получим дробь 1/n, которая и является числом, обратным натуральному числу n.

Итак, натуральному числу n обратным числом является число 1/n, то есть, дробь с числителем 1 и знаменателем n. Значит n и 1/n — взаимно обратные числа.

Отдельно отметим число, обратное натуральному числу 1. Число, обратное единице, это единица. Пара взаимно обратных чисел 1 и 1 уникальна тем, что составляющие ее числа равны, других таких пар взаимно обратных чисел не существует.

Найти число, обратное смешанному числу

Напомним, что смешанное число выглядит так: A b/c. Чтобы найти число, обратное смешанному числу, нужно представить данное смешанное число в виде неправильной дроби, а уже после найти число, обратное этой дроби. Как это работает рассмотрим на примере.

Пример

Найти число, обратное смешанному числу

Сначала выполним перевод смешанного числа в неправильную дробь:

Число, обратное дроби 65/9, есть дробь 9/65. Поэтому, смешанному числу 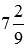обратно число 9/65.

Ответ: 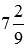и 9/65 взаимно обратные числа.

Найти число, обратное десятичной дроби

Конечную десятичную дробь или периодическую десятичную дробь можно заменить обыкновенной дробью. Поэтому найти число, обратное конечной или периодической десятичной дроби, можно через поиск числа, которое обратно обыкновенной дроби. Разберемся на примерах.

Пример 1

Найти число, которое обратно десятичной дроби 5,128.

Переведем конечную десятичную дробь в обыкновенную:

Числом, обратным полученной дроби, является обыкновенная дробь 125/641. Это и есть решение задачи.

Пример 2

Какое число является обратным для периодической десятичной дроби 2,(18)?

Переведем периодическую десятичную дробь в обыкновенную:

Обратная дробь для 24/11 — 11/24. Значит, числом, обратным исходной десятичной дроби 2,(18), является дробь 11/24.

Так как бесконечным непериодическим десятичным дробям отвечают иррациональные числа, то числа, которые обратны им, также записывают в виде дробных выражений.

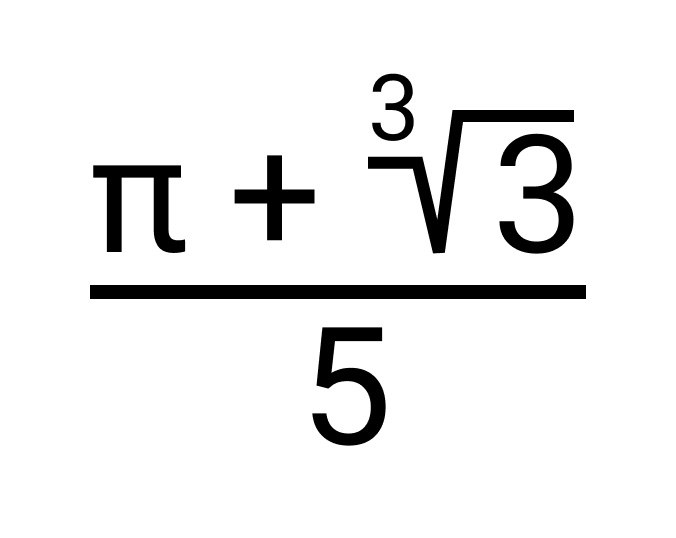
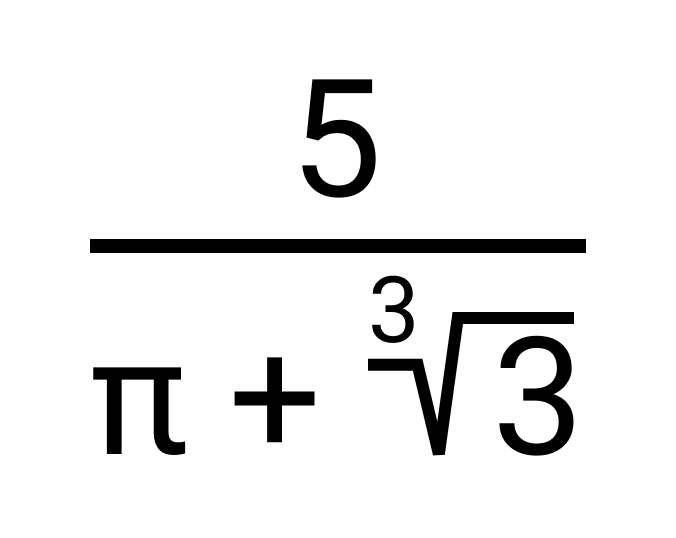
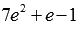
Например, иррациональному числу обратно число , а иррациональному числу обратно число

Взаимно обратные числа с корнями

Важно запомнить, что вид взаимно обратных чисел может отличаться от a и 1/a. Поэтому нужно быть внимательным. Особенно это касается чисел, записи которых содержат знак корня. Рассмотрим на примере, как это бывает.

Пример

Вычислим произведение этих чисел:

Так как в ответе мы получили единицу и мы знаем, что произведение взаимно обратных чисел равно 1, значит эти числа можно назвать взаимно обратными.

Ответ: да, число взаимно обратны.

Взаимно обратные числа со степенями

Допустим, есть число, которое равно какой-то степени числа a. То есть, число a возведено в степень b. Обратным числу ab будет число a-b. Проверим.

Пример

Взаимно обратные числа с логарифмами

У логарифма числа a по основанию b обратное число равно логарифму числа b по основанию a. То есть log _b a и log _a b — взаимно обратные числа.

Действительно, из свойств логарифма следует, что

, откуда log _b a * log _a b = 1.

Пример

Записать число, которое обратно логарифму числа 3 по основанию

Число, обратное числу 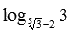, выглядит так:

Ответ:

Найти число, обратное комплексному числу

Сейчас узнаем, как находить число, обратное комплексному числу z.

Пример 1

Найти число, обратное комплексному числу 4 + i.

4 + i =

Умножим числитель и знаменатель полученного дробного выражения на число
4 + i.

Ответ:

или

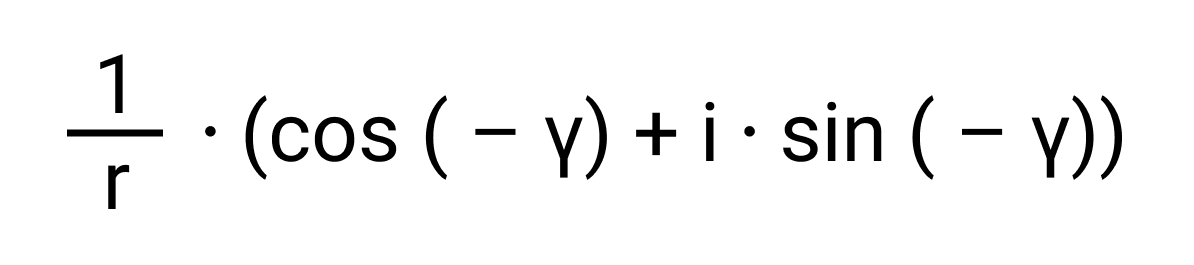
Действительно, и

Пример 2

Определить число, обратное комплексному числу

В этом примере r = 2 и 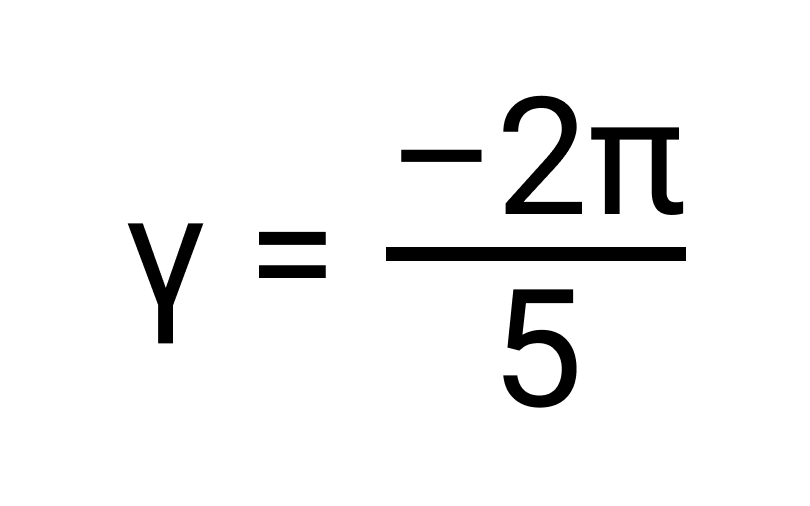, откуда 1/r = 1/2 и

Следовательно, нужное нам обратное число равно

Являются ли числа взаимно обратными? Да, мы только что это доказали.

Ответ:

Неравенство с суммой взаимно обратных чисел

В математике есть специальная теорема о сумме взаимно обратных чисел — давайте ее сформулируем и узнаем ключевое свойство.

Теорема

Сумма двух положительных взаимно обратных чисел больше или равна 2.

Доказательство теоремы:

Нам известно, что среднее арифметическое положительных чисел a и b всегда больше или равно среднему геометрическому этих чисел, то есть,

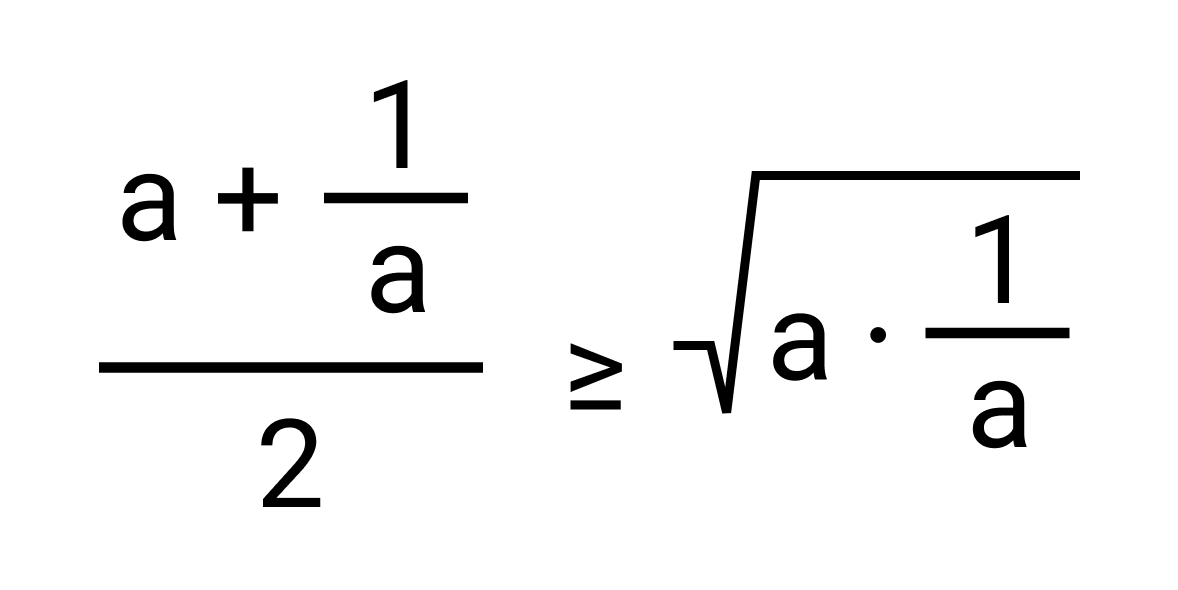
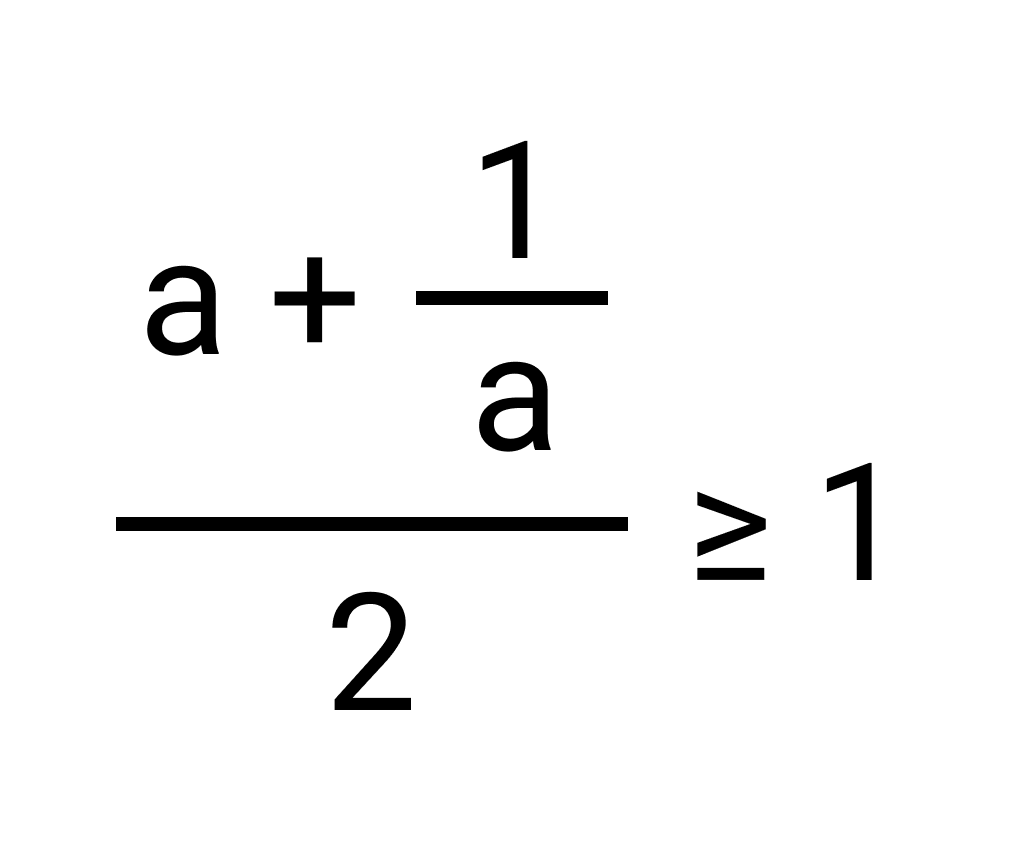
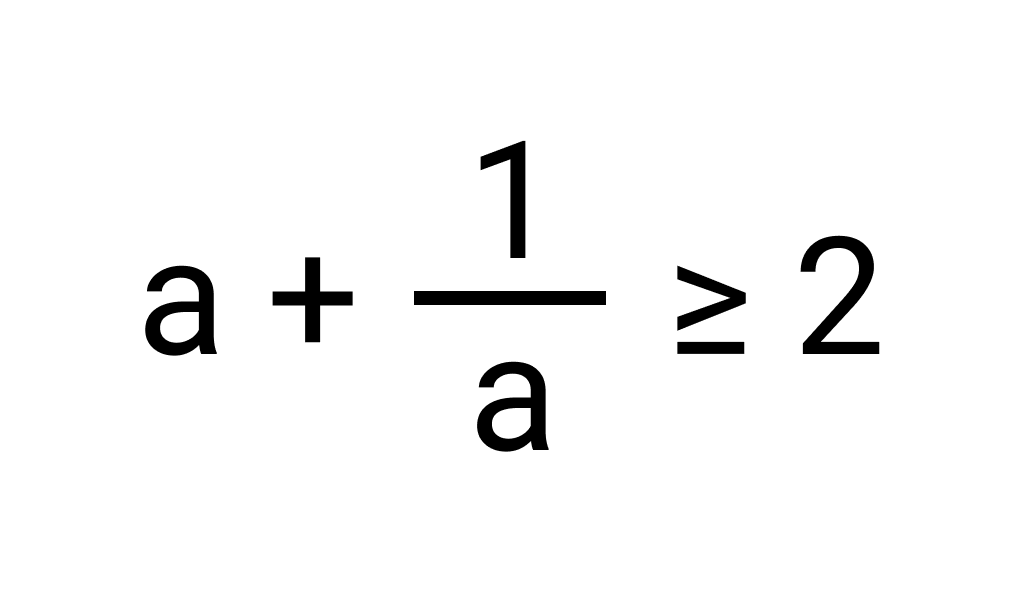
Если в качестве b мы возьмем число, обратное a, то полученное неравенство будет выглядеть так: откуда и , что и требовалось доказать.

Пример

Вычислить сумму взаимно обратных чисел 2/3 и 3/2,

Источник

Взаимно обратные числа, нахождение обратного числа.

Дадим определение и приведем примеры взаимно обратных чисел. Рассмотрим, как находить число, обратное натуральному числу и обратное обыкновенной дроби. Помимо этого, запишем и докажем неравенство, отражающее свойство суммы взаимно обратных чисел.

Взаимно обратные числа. Определение

Как найти число, обратное данному

Для натуральных чисел и обыкновенных дробей найти обратное число довольно просто. Можно сказать, даже очевидно. В случае нахождения числа, обратного иррациональному или комплексному числу, придется произвести ряд вычислений.

Рассмотрим наиболее часто встречающиеся на практике случаи нахождения обратного числа.

Число, обратное обыкновенной дроби

Число, обратное натуральному числу

Отдельное внимание стоит уделить единице, так как это единственное число, обратное число для которого равно ему самому.

Других пар взаимно обратных чисел, где обе составляющие равны, не существует.

Число, обратное смешанному числу

Число, обратное десятичной дроби

Десятичная дробь также можно представить в виде обыкновенной дроби. Нахождение обратного десятичной дроби числа сводится к представлению десятичной дроби в виде обыкновенной дроби и нахождению обратного числа для нее.

Рассмотрим еще один пример.

Пример. Нахождение числа, обратного десятичной дроби

Переводим десятичную дробь в обыкновенную:

Аналогично и для иррациональных чисел, отвечающим непериодическим бесконечным дробям, обратные числа записываются в виде дробных выражений.

Взаимно обратные числа с корнями

Обратимся к практике.

Пример. Взаимно обратные числа с корнями

Чтобы узнать, являются ли числа взаимно обратными, вычислим их произведение.

Произведение равно единице, значит, числа взаимно обратны.

Рассмотрим еще один пример.

Пример. Взаимно обратные числа с корнями

Взаимно обратные числа со степенями

Пример. Взаимно обратные числа со степенями

Взаимно обратные числа с логарифмами

Пример. Взаимно обратные числа с логарифмами

Число, обратное комплексному числу

Как уже отмечалось ранее, определение взаимно обратных чисел справедливо не только для действительных чисел, но и для комплексных.

Пример. Число, обратное комплексному числу

Помимо алгебраической формы, комплексное число может быть представлено в тригонометрической или показательной форме следующим образом:

z = r · cos φ + i · sin φ

Соответственно, обратное число будет иметь вид:

Рассмотрим примеры с представлением комплексных чисел в тригонометрической и показательной форме.

Пример. Найти число, обратное комплексному числу

Ответ: 1 2 · e i 2 π 5

Сумма взаимно обратных чисел. Неравенство

Существует теорема о сумме двух взаимно обратных чисел.

Сумма взаимно обратных чисел

Приведем доказательство теоремы. Как известно, для любых положительных чисел a и b среднее арифметическое больше или равно среднему геометрическому. Это можно записать в виде неравенства:

a + 1 a 2 ≥ a · 1 a a + 1 a ≥ 2

Что и требовалось доказать.

Приведем практический пример, иллюстрирующий данное свойство.

Пример. Найти сумму взаимно обратных чисел

Вычислим сумму чисел 2 3 и обратного ему числу.

2 3 + 3 2 = 4 + 9 6 = 13 6 = 2 1 6

Как и говорит теорема, полученное число больше двух.

Источник