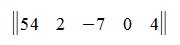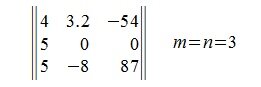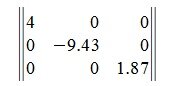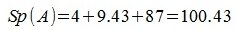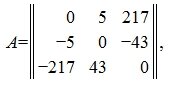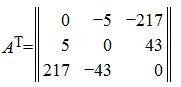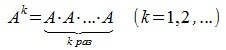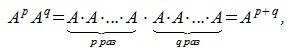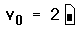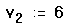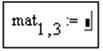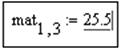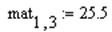Что значит нижний индекс у матрицы
Что значит нижний индекс у матрицы
Глава 3. Работа с векторами и матрицами
3.2 Нумерация элементов и определение параметров матрицы
Нумерация элементов матрицы
Элементы матрицы определяются двумя нижними индексами, элементы вектора – одним.
Для ввода нижнего индекса можно щелкнуть в математической панели на кнопке х n Subscript (Нижний индекс), но лучше использовать клавишу [ (открывающаяся квадратная скобка), так как во время работы с матрицами вводить нижний индекс приходится очень часто.
Чтобы из матрицы выделить вектор (один из столбцов матрицы), используется верхний индекс. Эта операция применяется не очень часто, поэтому для ее выполнения лучше использовать математическую панель инструментов:
– Введите имя матрицы и выделите его синим уголком курсора.
– В математическом меню щелкните на кнопке Matrix and Vector Toolbar (Панель векторов и матриц) и щелкните на кнопке M Matrix Column (Столбец матрицы).
– В появившемся месте ввода пишите номер столбца.
Встроенная переменная ORIGIN
По умолчанию ORIGIN =0, то есть первый элемент вектора, первая строка и первый столбец матрицы имеют индекс ноль.
Чтобы изменить нумерацию индексов в первой строке документа, наберите (прописными буквами) ORIGIN :=1. Можно переопределить встроенную переменную ORIGIN другим способом. Выберите в главном меню команду Tools → Worksheet Options (Инструменты→Параметры документа), в открывшемся окне перейдите на вкладку Built – In Variables → ORIGIN (Встроенные переменные) и в поле Array Origin ( ORIGIN ) введите индекс первого элемента массива (рис.4.2). Переменной ORIGIN можно присваивать разные значения, в том числе отрицательные.

Определение параметров матрицы
В MathCAD есть встроенные функции для определения параметров матрицы (рис. 3.4 ):
– rows ( M ) – число строк в массиве или векторе;
– cols ( M ) – число строк в массиве;
– last ( M ) – индекс последнего элемента в векторе;
– max ( M ) и min ( M ) – максимальное и минимальное значения элементов в массиве
– сумма элементов вектора вычисляется нажатием кнопки ∑ V на панели Matrix ;
– tr ( M ) – сумма диагональных элементов квадратной матрицы, называемая следом матрицы, где M – имя матрицы.


число строк в массиве 
число столбцов в массиве 
индекс последнего элемента в векторе
max и min элементы в массиве


Рис. 3. 4 Функции определения параметров массивов
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или 
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
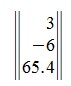
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Побочная диагональ матрицы
Диагональная матрица
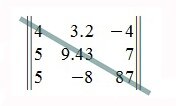
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
След матрицы
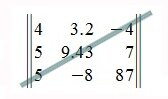
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
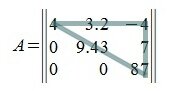
Верхняя треугольная матрица
Нижняя треугольная матрица
Квадратная матрица 
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
Для обозначения разности двух матриц используется запись:
Степень матрицы
Пусть 
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.
Для симметричных матриц 
Знакомство с матрицами
Понятие и базовые операции.
Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.
Что такое матрица
Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.
Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.
Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.
В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.


Простые операции с матрицами
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.
И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.


Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

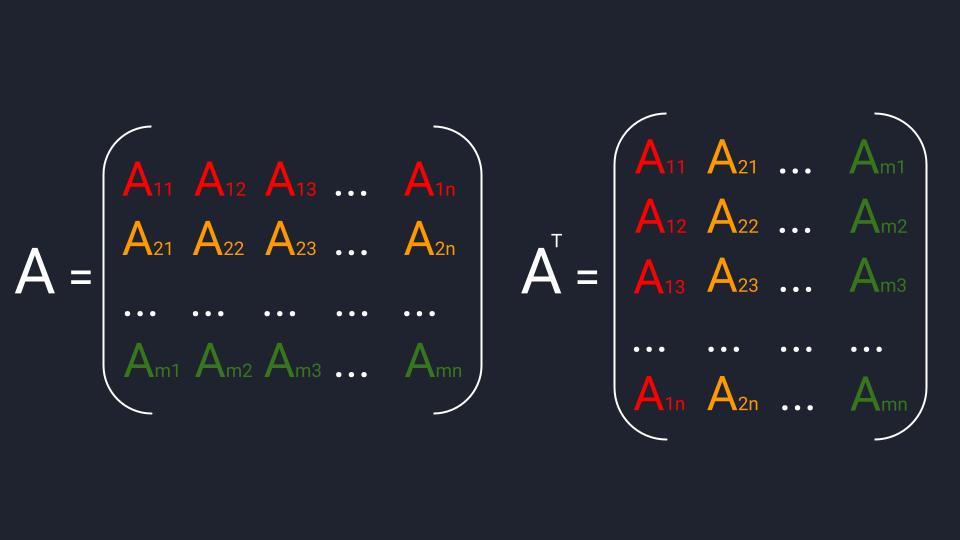
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.
⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

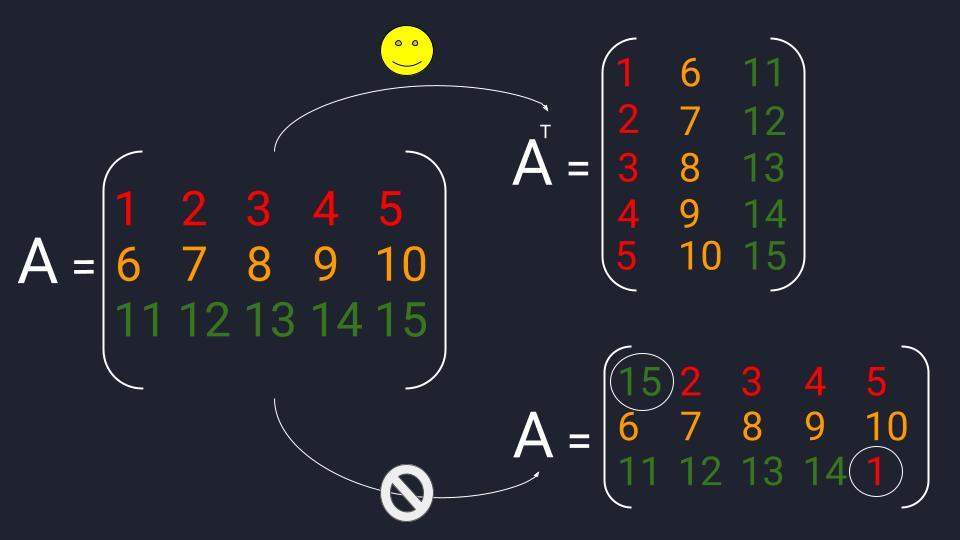
Сложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.


Умножение матриц
Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.
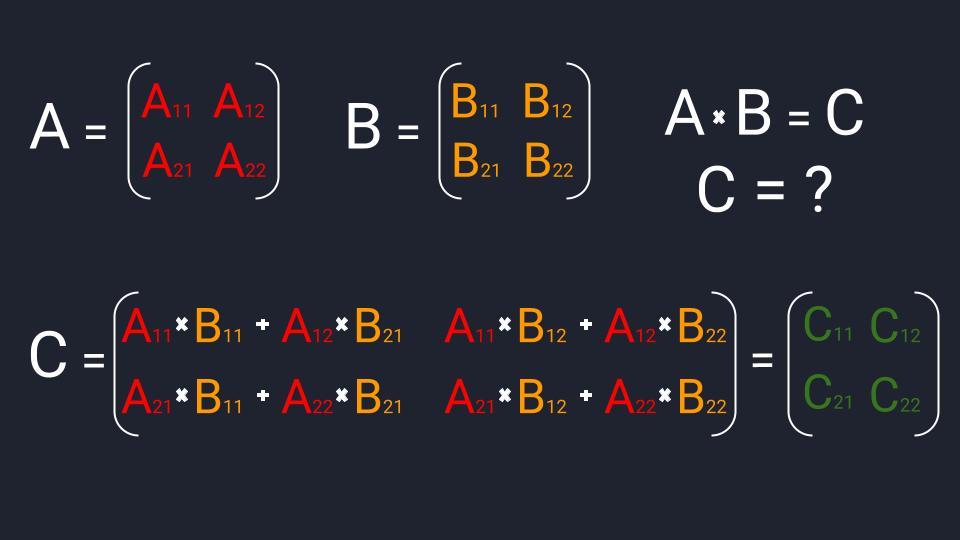

Что дальше
В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽
Что значит нижний индекс у матрицы
Можно обращаться к отдельным элементам массива, используя нижние индексы. Можно также обращаться к отдельному столбцу массива, используя верхний индекс. Чтобы напечатать нижний индекс, используйте клавишу левой скобки [ и поместите в поле целое число или пару целых чисел. Чтобы вставить оператор верхнего индекса, нажмите [Ctrl]6 и поместите в поле целое число.
Вектор и элементы матрицы обычно нумеруются, начиная с нулевой строки и нулевого столбца. Чтобы изменить этот порядок, замените значение встроенной переменной ORIGIN.
Нижние индексы и элементы вектора
Рисунок 2 показывает, как это выглядит.
Когда определяются элементы вектора, часть из них можно оставлять неопределенными. Например, если v не был определен, и определяется равным 10, то v0, v1, и v2 все окажутся неопределенными. Mathcad заполняет эти элементы нулями, пока в них не будут внесены необходимые значения. Иллюстрация этого приведена на Рисунке 3. Будьте внимательны: так можно нечаянно создать очень большие векторы и матрицы.
Рисунок 3: Mathcad заполняет нулями все элементы, которые явно не определены.
Нижние индексы и элементы матрицы
Обратите внимание, что нижние индексы, подобно делению и возведению в степень удерживают ввод. Что бы ни печаталось после [, всё остается в нижнем индексе, пока не будет нажат [Space], чтобы выйти оттуда.
Рисунок 4 показывает некоторые примеры того, как определить отдельные элементы матрицы и как просмотреть их. Обратите внимание, что, как и в случае с векторами, Mathcad заполняет неопределенные элементы матрицы нулями.
Можно также определять элементы вектора или матрицы формулой типа vi :=i, где i — дискретный аргумент. См. следующую главу “Дискретные аргументы”.
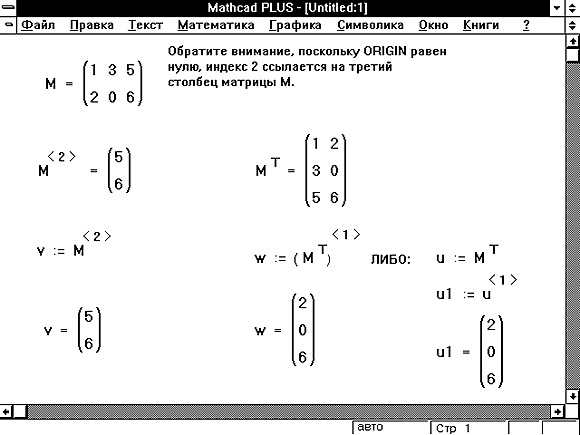
Рисунок 4: Определение и просмотр элементов матрицы.
Рисунок 5: Использование оператора верхнего индекса для извлечения столбца из матрицы.
Верхние индексы и столбцы матрицы
Чтобы обратиться ко всему столбцу массива, нажмите [Ctrl]6 и поместите номер столбца в появившееся поле. Рисунок 5 ниже показывает, как присвоить вектору v значение третьего столбца матрицы M.
Можно также извлекать отдельную строку из матрицы, извлекая столбец из транспонированной матрицы. Иллюстрация этого приведена на Рисунке 5.
Изменение значения ORIGIN
По умолчанию массивы Mathcad нумеруются с нулевого элемента. Чтобы изменить этот порядок, замените значение встроенной переменной ORIGIN. Когда используются нижние индексы, Mathcad учитывает, что массивы нумеруются начиная с принятого значения ORIGIN.
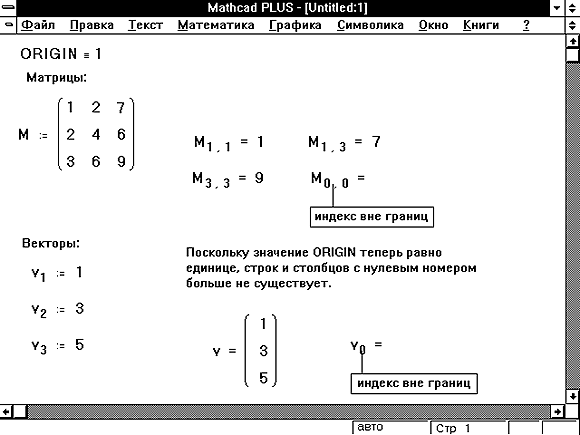
Рисунок 6: Массивы, нумерующиеся с первого элемента вместо нулевого.
Если изменить ORIGIN на 1, Mathcad больше не будет воспринимать нулевой элемент для векторов или нулевые строки и столбцы для матриц. Рисунок 6 показывает рабочий документ с ORIGIN, равным 1. Заметьте, что при попытке обращения к Mathcad теперь сообщает об ошибке “индекс вне границ”.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Нижние индексы и элементы матрицы и вектора
Нижний индекс используется для просмотра и определения элементов матрицы.
q Ввести имя матрицы, например, mat
q Ввести нижний индекс, 
Варианты ввода нижнего индекса.
| Пиктограмма | 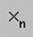 в панели инструментов Matrix (Матрица) в панели инструментов Matrix (Матрица) |
| Клавиатура | клавиша «[« |
Следует отметить, что не надо путать нижней индекс в имени переменной (длина курсора при переходе на нижней индекс в имени переменной при этом не меняется) и нижний индекс в определении элемента массива (длина курсора при переходе на нижней индекс в имени переменной при этом уменьшается)
q Ввести в черном прямоугольнике номер строки и через запятую номер столбца, например 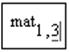
q Ввести знак присвоения, нажав клавиши Shift + «:»,
q Ввести присваиваемое значение, например
q Нажать клавишу «Enter» для завершения операции