Чем отличается непрерывный сигнал от дискретного

Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные (НС) и дискретные сигналы (ДС).

Особенности непрерывного сигнала

Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом

Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции. Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.

Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:

Что такое дискретный

Дискретность применяется в вычислительной технике для пакетной передачи данных

Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.

Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС. В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.

Достоинствами цифровых систем, работающих на ДС, являются:

Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно. Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.

Отличия двух видов сигналов

Все значения дискретного сигнала можно пронумеровать целыми числами

Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.

К недостаткам систем, использующих ДС, можно отнести:

Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее. Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.

Источник

INFOблог

Поиск по этому блогу

воскресенье, 8 сентября 2013 г.

Непрерывные и дискретные сигналы

Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации , а изменение какой-либо характеристики носителя мы будем называть сигналом .
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).

При этом сигналы могут быть двух видов: непрерывный (или аналоговый ) и дискретный .
В учебнике даны следующие определения.

Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.

Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.

Источник

Аналоговые, дискретные и цифровые сигналы

Любая физическая величина по характеру изменения ее значения может быть постоянной (если она имеет только одно фиксированное значение), дискретной (если она может иметь два или более фиксированных значений), или аналоговой (если она может иметь бесчисленное множество значений). Все эти величины могут быть преобразованы в цифровую форму.

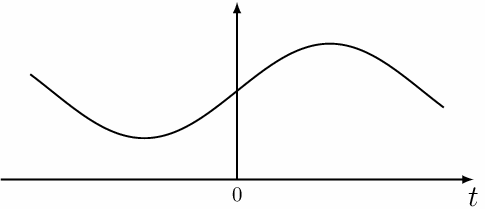
Аналоговым называется такой сигнал, который может быть представлен непрерывной линией из множества значений, определенных в каждый момент времени относительно временной оси.

Значения аналогового сигнала произвольны в каждый момент времени, поэтому он может быть в принципе представлен как некая непрерывная функция (зависящая от времени как от переменной) либо как кусочно-непрерывная функция времени.

Аналоговым сигналом можно назвать, например, звуковой сигнал, генерируемый обмоткой электромагнитного микрофона или ламповым акустическим усилителем, поскольку такой сигнал непрерывен и его значения (напряжение или ток) сильно отличаются друг от друга в каждый момент времени.

На приведенном ниже рисунке изображен пример подобного рода аналогового сигнала.

Аналоговые величины могу иметь бесконечное множество значений в определенных пределах. Они непрерывны и их значения не могут изменяться скачками.

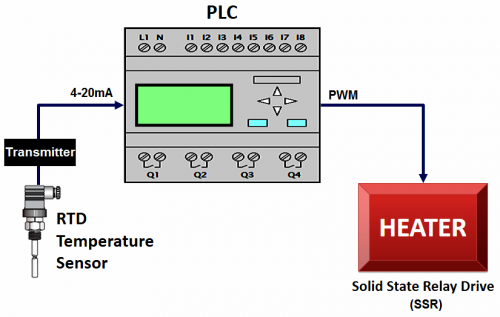
Пример аналогового сигнала: термопара передает в аналоговом виде значение температуры в программируемый логический контроллер, который управляет с помощью твердотельного реле температурой в электрической печи.

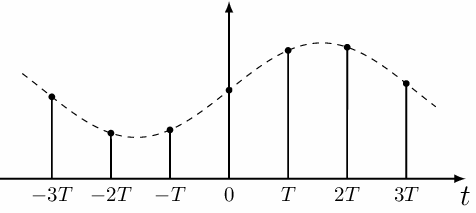
Если некий сигнал принимает произвольные значения лишь в отдельные моменты времени, то такой сигнал называют дискретным. Чаще всего на практике применяются дискретные сигналы, распределенные по равномерной временной решетке, шаг которой называется интервалом дискретизации.

Дискретный сигнал принимает определенные не нулевые значения лишь в моменты дискретизации, то есть он является не непрерывным в отличие от аналогового сигнала. Если из звукового сигнала вырезать небольшие кусочки определенного размера через равные интервалы, такой сигнал можно будет назвать дискретным.

Ниже приведен пример формирования подобного дискретного сигнала с интервалом дискретизации Т. Обратите внимание, что квантуется лишь интервал дискретизации, но не сами значения сигнала.

Дискретные сигналы имеют два и более фиксированных значений (количество их значений всегда выражается целыми числами).

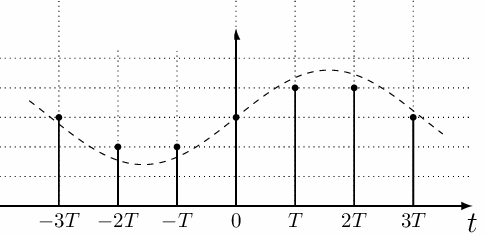
Когда дискретный сигнал принимает только какие-то фиксированные значения (которые могут быть расположены по сетке с определенным шагом), такие что они могут быть представлены как количество квантовых величин, такой дискретный сигнал называется цифровым. То есть цифровой сигнал — это такой дискретный сигнал, который квантован не только по промежуткам времени, но и по уровню.

Практически дискретные и цифровые сигналы в ряде задач отождествляются, и могут быть легко заданы в форме отсчетов с помощью вычислительного устройства.

На рисунке приведен пример формирования цифрового сигнала на базе аналогового. Обратите внимание, что значения цифрового сигнала не могут принимать промежуточных значений, а только определенные — целое количество вертикальных шагов сетки.

Цифровой сигнал легко записывается и перезаписывается в память вычислительных устройств, просто считывается и копируется без потери точности, тогда как перезапись аналогового сигнала всегда сопряжена с утратой некоторой, пусть и незначительной, части информации.

Обработка цифровых сигналов позволяет получать устройства с очень высокими характеристиками благодаря выполнению вычислительных операций совершенно без потерь качества, либо с пренебрежимо малыми потерями.

В силу этих достоинств, именно цифровые сигналы повсеместно распространены сегодня в системах хранения и обработки данных. Вся современная память — цифровая. Аналоговые носители информации (такие как пленочные кассеты и т.д.) давно ушли в прошлое.

Аналоговый и цифровой приборы для измерения напряжения:

Но даже у цифровых сигналов есть свои недостатки. Их невозможно передать напрямую как есть, ибо передача обычно реализуется посредством непрерывных электромагнитных волн. Поэтому при передаче и приеме цифровых сигналов необходимо прибегать к дополнительной модуляции и аналого-цифровому преобразованию. Меньший динамический диапазон цифровых сигналов (отношение наибольшего значения к наименьшему), обусловленный квантованностью значений по сетке, является еще одним их недостатком.

Существуют и такие области, где аналоговые сигналы незаменимы. Например аналоговый звук никогда не сравнится с цифровым, поэтому ламповые усилители и пластинки до сих пор не выходят из моды, несмотря на обилие цифровых форматов записи звука с самой высокой частотой дискретизации.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Основы цифровой обработки сигналов

Сигнал это изменение физической величины во времени или пространстве. К примеру, это может быть изменение одномерного сигнала в зависимости от времени. Если мы рассматриваем цифровое изображение это может быть изменение яркости пикселей в зависимости от его положения в пространстве.

Но с точки зрения математики сигнал это функция одной или нескольких независимых переменных. В нашем случае независимыми переменными являются время и положение в пространстве, а зависимыми переменными могут быть значения нашего сигнала x от t или яркости пикселей на цифровом изображении.

Непрерывные и дискретные сигналы:

Непрерывный аналоговый сигнал определен на всем промежутке времени, то есть мы в любой момент времени t можем узнать значение сигнала x. Если мы возьмем эти значения с периодом дискретизации T, то мы получаем дискретный сигнал, значение которого определены только в конкретные моменты времени.

Дискретный сигнал теперь записываем как x[n], и n это номера отчетов дискретной последовательности. Если взглянуть на процесс дискретизации с точки зрения математики, то выходная дискретная последовательность с x[n] формируется, когда мы подставляем в нашу функцию x(t) значение времени t равный nT, где n — это номер дискретного отчета, а T — это период дискретизации.

Периодические сигналы

Периодический сигнал это сигнал, форма которого повторяется во времени. Повторяться во времени может, как форма непрерывных сигналов, так и форма дискретных сигналов. Периодом сигнала называем интервал повторения.

К примеру, у дискретного сигнала y[n] форма повторяется каждые 4, 8, 12 и так далее отчетов, для непрерывного сигнала z[t] форма повторяется каждые 2, 4, 6 и так далее секунд.

Фундаментальным или основным периодом сигналом называется наименьший интервал повторения, то есть для нашего дискретного сигнала y[n] это 4 отчета, а для нашего непрерывно сигнала это две секунды.

Фундаментальная частота

От понятие фундаментального периода мы можем перейти к понятию фундаментальной частоты. Фундаментальная или основная частота также именуемая первая гармоника, это количество основных периода сигнала, приходящихся на единицу времени. Частота измеряется в Герцах, то есть в количестве периодов приходящейся на одну секунду, и фактически является обратной величиной основного периода.

Если мы рассмотрим наш непрерывный сигнал z[t] его основной период равен двум секундам, а это значит, что на одну секунду приходится ровно половина его периода.

Основная частота дискретного сигнала

Но если с непрерывным сигналом все более менее понятно, то есть можем взглянуть на него на временной оси, оценить величины основного периода и подсчитать значение основной частоты, то с дискретным сигналом все не так просто.

Нам доступны значение отчетов, мы знаем их номера в последовательности, но мы не знаем, как они соотносятся с его фундаментальной частотой, и как они соотносятся с частотой дискретизации. Давайте в этом попробуем разобраться на примере.

Возьмем дискретный сигнал, который мы используем для описания в предыдущих статьях. Он имеет период в 4 отчета, где два первых отчета в периоде имеют большую амплитуду, а два последних отчета имеют малую амплитуду.

Нашей задачи в данном примере будет при помощи такого сигнала услышать ноту ля первой октавы, то есть частоту 440 Гц. Для того чтобы это сделать нам обязательно надо понять, как основная частота соотносится с частотой дискретизации сигнала.

Для этого давайте перенесем наш сигнал на временную ось. Основной период данного сигнала высчитывается также, как для непрерывного сигнала, то есть это обратная величина его фундаментальной частоты, в нашем случае единицы делить на 440. Но мы также видим то, что период дискретизации нашего сигнала, обозначим здесь его как ∆t в 4 раза меньше, чем основной период, так как на основной период приходится ровно 4 отсчета.

Выразим частоту дискретизации через период дискретизации, частоту дискретизации можно записать, как единицу делить на ∆t, что получить равно 4 делить на T₀, то есть в нашем случае частота дискретизации должна быть в 4 раза больше, чем наша фундаментальная частота ноты ля первой октавы.

Изменение частоты дискретизации

Если мы рассмотрим наши манипуляции над дискретным сигналом, как манипуляции на аналоговом сигнале, а после этого дискретизацию аналогового сигнала, то вот к чему мы приходим. Когда мы увеличиваем частоту дискретизации, то мы фактически берем дискретные отчеты более быстрого аналогового сигнала, или кладем отчеты того же дискретного сигнала на другую временную сетку.

К примеру, наш дискретный сигнал с периодом дискретизации ∆t можно представить как оцифрованные значения аналогового сигнала с периодом Т₀,

Если теперь те же самые отчеты сигнала, мы положим на более плотную временную сетку с меньшим периодом ∆t, это фактически то же самое как если мы оцифровали более быстрый аналоговый сигнал с меньшим периодом Т₀.

В качестве эталонного, аналогового сигнала мы представили синусоиду, а почему мы так часто используем синусоиду, когда говорим о цифровой обработки сигналов об этом в следующей статье.

Источник

Чем отличается непрерывный сигнал от дискретного

Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные (НС) и дискретные сигналы (ДС).

Особенности непрерывного сигнала

Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом

Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции. Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.

Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:

Что такое дискретный

Дискретность применяется в вычислительной технике для пакетной передачи данных

Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.

Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС. В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.

Достоинствами цифровых систем, работающих на ДС, являются:

Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно. Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.

Отличия двух видов сигналов

Все значения дискретного сигнала можно пронумеровать целыми числами

Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.

К недостаткам систем, использующих ДС, можно отнести:

Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее. Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.

Источник