Что значит неположительное число и неотрицательное
Целые числа
Вы будете перенаправлены на Автор24
Что значит целое число
Итак, рассмотрим, какие числа называют целыми.
Если вспомнить курс математики, то целыми числами являются натуральные числа, нуль и числа, противоположные натуральным.
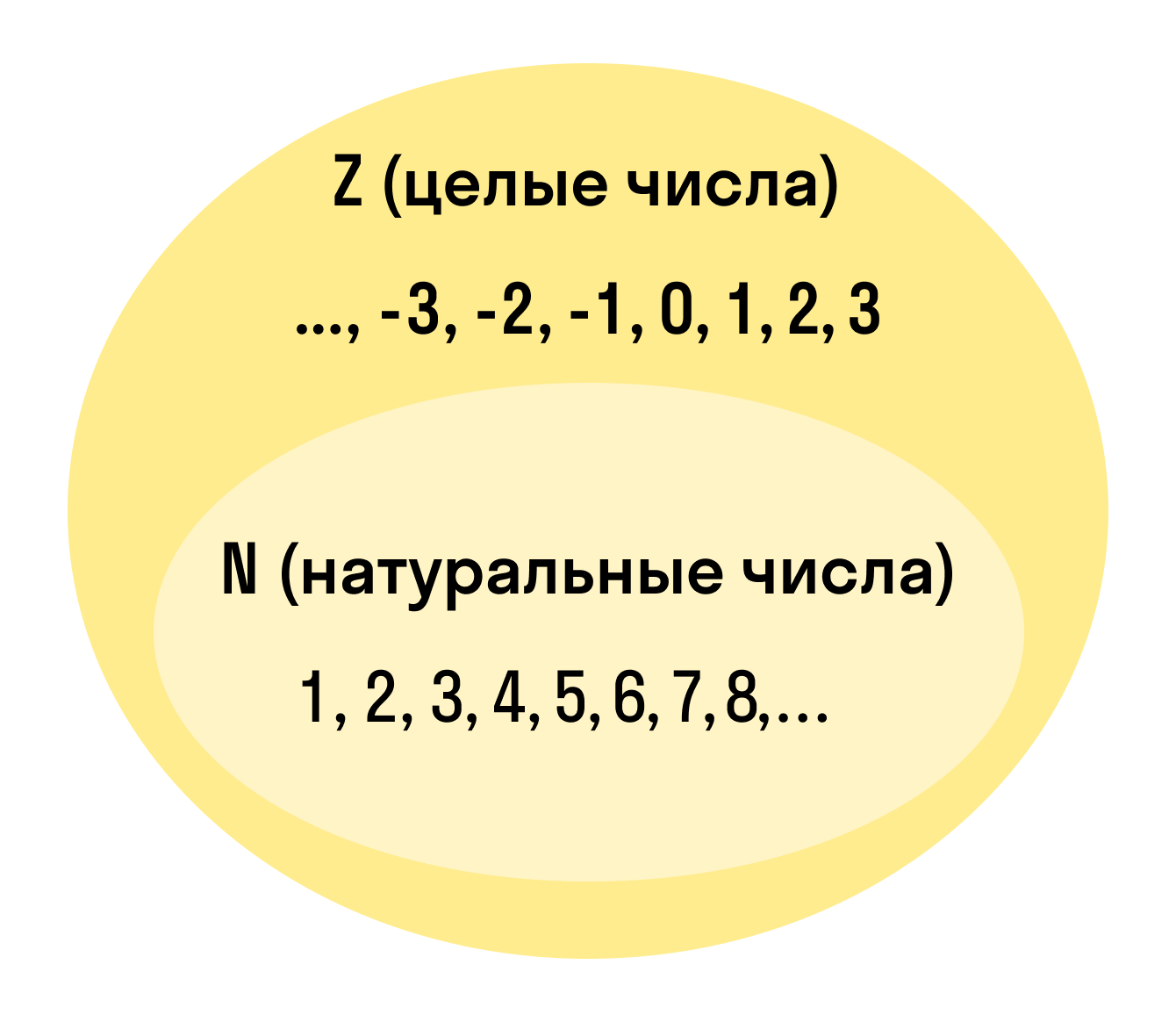
Множество натуральных чисел есть подмножеством множества целых чисел, т.е. любое натуральное будет являться целым числом, но не любое целое является натуральным числом.
Целые положительные и целые отрицательные числа
Целыми положительными числами являются целые числа со знаком плюс.
Целыми отрицательными числами являются целые числа со знаком минус.
Число ноль не относится ни к целым положительным, ни к целым отрицательным числам.
Целыми положительными числами являются целые числа, большие нуля.
Целыми отрицательными числами являются целые числа, меньшие нуля.
Множество натуральных целых чисел являет собой множество всех целых положительных чисел, а множество всех противоположных натуральным числам являет собой множество всех целых отрицательных чисел.
Целые неположительные и целые неотрицательные числа
Все целые положительные числа и число нуль называются целыми неотрицательными числами.
Готовые работы на аналогичную тему
Таким образом, целым неотрицательным числом являются целые числа, большие нуля или равные нулю, а целым неположительным числом – целые числа, меньшие нуля или равные нулю.
Описание изменения величин при помощи целых чисел
Целые числа применяются для описания изменения числа каких-либо предметов.
Целые числа удобно использовать, т.к. не нужно явное указание на увеличение числа или уменьшение, – знак целого числа указывает на направление изменения, а значение – на количественное изменение.
С помощью целых чисел можно выразить не только изменение количества, но и изменение любой величины.
Рассмотрим пример изменения стоимости товара.
Отдельно рассмотрим значение отрицательных целых чисел как размера долга.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 08 06 2021
Какие числа называются целыми
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение целых чисел
Что важно знать о целых числах:
Целые числа на числовой оси выглядят так:
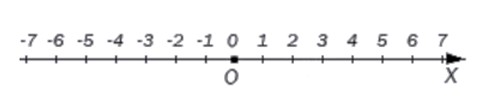
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Целые числа: общее представление
В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.
Целые числа. Определение, примеры
Определение 1. Целые числа
Целые числа и координатная прямая
Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.
В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.
Положительные и отрицательные целые числа
Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.
Определение 2. Положительные целые числа
Определение 3. Отрицательные целые числа
Число 0 разделяет положительные и отрицательные целые числа и само не является ни положительным, ни отрицательным.
Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число.
Можно дать другие формулировки определений отрицательных и положительных целых чисел, используя их сравнение с нулем.
Определение 4. Положительные целые числа
Соответственно, положительные числа лежат правее начала отсчета на координатной прямой, а отрицательные целые числа находятся левее от нуля.
Неположительные и неотрицательные целые числа
Определение 6. Неотрицательные целые числа
Как видим, число нуль не является ни положительным, ни отрицательным.
Использование целых чисел при описании изменения величин
Для чего используются целые числа? В первую очередь, с их помощью удобно описывать и определять изменение количества каких-либо предметов. Приведем пример.
Пусть на складе хранится какое-то количество коленвалов. Если на склад привезут еще 500 коленвалов, то их количество увеличится. Число 500 как раз и выражает изменение (увеличение) количества деталей. Если потом со склада увезут 200 деталей, то это число также будет характеризовать изменение количества коленвалов. На этот раз, в сторону уменьшения.
Если же со склада ничего не будут забирать, и ничего не будут привозить, то число 0 укажет на неизменность количества деталей.
Очевидное удобство использования целых чисел в отличие от натуральных в том, что их знак явно указывает на направление изменения величины (увеличение или убывание).
Неотрицательное число
Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Содержание
Свойства отрицательных чисел
Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.
Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).
Общее представление о целых числах.
Информация этой статьи формирует общее представление о целых числах. Сначала дано определение целых чисел и приведены примеры. Далее рассмотрены целые числа на числовой прямой, откуда становится видно, какие числа называются целыми положительными числами, а какие – целыми отрицательными. После этого показано, как при помощи целых чисел описываются изменения величин, и рассмотрены целые отрицательные числа в смысле задолженности.
Навигация по странице.
Целые числа – определение и примеры
Дадим определение целых чисел. Чтобы его понять, нужно знать про натуральные числа, а также иметь представление о противоположных числах.
Целые числа – это натуральные числа, число нуль, а также числа, противоположные натуральным.
Все целые числа удобно представлять как последовательность целых чисел, которая имеет следующий вид: 0, ±1, ±2, ±3, … Последовательность целых чисел можно записать и так: …, −3, −2, −1, 0, 1, 2, 3, …
Из определения целых чисел следует, что множество натуральных чисел является подмножеством множества целых чисел. Поэтому, любое натуральное число является целым, но не любое целое число является натуральным.
Целые числа на координатной прямой
Давайте взглянем на координатную прямую, чтобы увидеть точки, соответствующие целым числам. Будем считать, что координатная прямая проведена горизонтально и направлена вправо.
Из построения координатной прямой следует, что началу отсчета и точкам, отмеченным штрихами, взаимно однозначно соответствуют целые числа. То есть, каждой из указанных точек соответствует единственное целое число, следовательно, несовпадающим точкам отвечают разные целые числа. Началу отсчета (точке O ) соответствует целое число нуль, а точкам, которые отмечены штрихами, соответствуют другие целые числа. Никаким другим точкам координатной прямой целые числа не соответствуют, и никакому целому числу не отвечает точка координатной прямой, отличная от указанных выше.
В любую точку, отмеченную штрихом (координатами этих точек являются целые числа), мы можем попасть, если от начала отсчета последовательно отложим некоторое количество единичных отрезков.
Целые положительные и целые отрицательные числа
Изучив материал статьи положительные и отрицательные числа, мы из всех целых чисел можем выделить целые положительные и целые отрицательные числа.
Целые отрицательные числа – это целые числа со знаком минус.
Число нуль (число 0 ) не является ни целым положительным, ни целым отрицательным числом. Нуль как бы отделяет целые отрицательные числа от целых положительных.
Вообще, в силу определения противоположных чисел, любое число, противоположное целому положительному числу, есть целое отрицательное число. И наоборот, любое число, противоположное целому отрицательному числу, есть целое положительное. Это утверждение позволяет дать определения целых положительных и целых отрицательных чисел на основе их сравнения с нулем (здесь нужно владеть материалом статьи сравнение целых чисел).
Целые положительные числа – это целые числа, которые больше нуля.
Целые отрицательные числа – это целые числа, которые меньше нуля.
Понятно, что множество всех целых положительных чисел представляет собой множество натуральных чисел. В свою очередь множество всех целых отрицательных чисел – это множество всех чисел, противоположных натуральным числам.
Отдельно обратим Ваше внимание на то, что любое натуральное число мы можем смело назвать целым, а любое целое число мы НЕ можем назвать натуральным. Натуральным мы можем назвать лишь любое целое положительное число, так как целые отрицательные числа и нуль не являются натуральными.
Целые неположительные и целые неотрицательные числа
Дадим определения целых неположительных чисел и целых неотрицательных чисел.
Все целые положительные числа вместе с числом нуль называют целыми неотрицательными числами.
Другими словами, целое неотрицательное число – это целое число, которое больше нуля, либо равно нулю, а целое неположительное число – это целое число, которое меньше нуля, либо равно нулю.
Наиболее часто термины «целые неположительные числа» и «целые неотрицательные числа» используют для краткости изложения. Например, вместо фразы «число a целое, причем a больше нуля или равно нулю» можно сказать « a – целое неотрицательное число».
Описание изменения величин при помощи целых чисел
Пришло время поговорить о том, для чего вообще нужны целые числа.
Основное предназначение целых чисел заключается в том, что с их помощью удобно описывать изменение количества каких-либо предметов. Разберемся с этим на примерах.
Пусть на складе находится некоторое количество деталей. Если на склад привезут еще, к примеру, 400 деталей, то количество деталей на складе увеличится, а число 400 выражает это изменение количества в положительную сторону (в сторону увеличения). Если же со склада заберут, например, 100 деталей, то количество деталей на складе уменьшится, а число 100 будет выражать изменение количества в отрицательную сторону (в сторону уменьшения). На склад не будут привозить детали, и не будут увозить детали со склада, то можно говорить о неизменности количестве деталей (то есть можно будет говорить о нулевом изменении количества).
Целые числа также могут выражать не только изменение количества, но и изменение какой-либо величины. Разберемся с этим на примере изменения температуры.