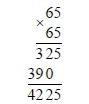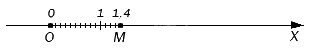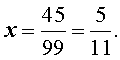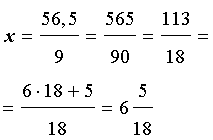Что значит непериодическая десятичная дробь
Бесконечные дроби и иррациональные числа
теория по математике 📈 числа и вычисления
При переводе обыкновенной дроби в десятичную можно получить конечную периодическую или бесконечную десятичные дроби (кроме простой десятичной, разумеется).
Конечная десятичная дробь
Конечная десятичная дробь – десятичная дробь с конечным числом знаков после запятой, то есть когда у аналога обыкновенной дроби числитель без остатка делится на знаменатель.
Пример №1. ¾ — делим 3 на 4 и получаем 0,75.
Пример №2. 31 /50 делим 31 на 50 и получаем 0,62.
Пример №3. 3 /25 делим 3 на 25 и получаем 0,12.
Периодическая десятичная дробь
Периодическая десятичная дробь – дробь, у которой после запятой (в дробной части) присутствует бесконечный повтор одной цифры или сочетания нескольких одинаковых цифр.
Пример №4. 7 /12 При делении 7 на 12 получается 0,5833333…, где постоянно повторяется цифра 3, запись делают следующим образом: 0,58(3); читается эта дробь следующим образом: нуль целых пятьдесят восемь сотых и три в периоде.
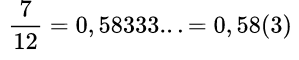
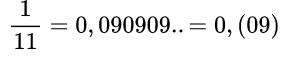
Иррациональные числа — числа, которые не могут быть представлены в виде обыкновенной дроби.
Значение какого из выражений является рациональным числом?
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
Данный вариант ответа нам подходит.
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных чисел является рациональным?
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
Рассмотри каждое из них:
Следовательно, число √0,81 является рациональным, остальные же числа
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
pазбирался: Даниил Романович | обсудить разбор | оценить
Значение какого из данных ниже выражений является наибольшим?
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
Переносим 3 под корень:
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
Возводим 6,5 в квадрат:
Посмотрим на все получившиеся варианты:
Следовательно, правильный ответ первый.
pазбирался: Даниил Романович | обсудить разбор | оценить
Для решения этого задания достаточно представлять себе значения чисел меньше и больше заданного, корни которых подлежат вычислению.
Значит, нам подходит третий вариант ответа — √38.
pазбирался: Даниил Романович | обсудить разбор | оценить
Математика. 6 класс
Конспект урока
Непериодические десятичные дроби
Перечень рассматриваемых вопросов:
Рациональное число, можно записать в виде конечной или бесконечной периодической десятичной дроби.
Существуют бесконечные непериодические десятичные дроби. Например, дроби 0,010010001…; 17,12345678910…
Бесконечные десятичные дроби называют числами.
Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.
Рациональные и иррациональные числа называются действительными числами.
Теоретический материал для самостоятельного изучения
Рассмотрим положительную бесконечную десятичную дробь 0,1011011101111…
У этой дроби нет группы цифр, являющейся периодом. Эта дробь непериодическая.
Примеры бесконечных непериодических дробей
Поставив перед положительной дробью знак «–», получим отрицательную дробь.
является отрицательной бесконечной непериодической дробью.
Обнаружены новые числа, которые раньше не встречались. Эти новые для вас числа называют иррациональными.
Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.
Рациональные и иррациональные числа называются действительными числами.
Любое действительное число представляется в виде бесконечной десятичной дроби.
Если число – рациональное, то дробь – периодическая, а если иррациональное, то дробь – непериодическая.
Считается, что иррациональные числа были открыты в Древней Греции приблизительно за 400 лет до нашей эры. Самое знаменитое иррациональное число пи обозначается греческой буквой – π и приближенно равно 3,141592653589793238462643.
Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют «День числа пи». В этот день даже проводятся соревнования по запоминанию десятичных знаков этого числа.
Что мы знаем о числах?
Рассмотрим, как выполняются действия с действительными числами. На практике бесконечные десятичные дроби складывают, вычитают, умножают и делят приближенно.
Пример 1. Сравните: 0,(23) и 0,1234…
Чтобы сравнить дроби надо уравнять количество десятичных знаков и затем сравнить.
Пример 2. Найдем приближенную сумму и разность чисел а и b, округлив их с точностью до одной десятой, если а = 23,(18), b = – 4,23(75).
Решение: округляя эти числа с точностью до одной десятой, находим, что а ≈ 23,2 и b = – 4,2. Тогда а + b ≈ 19,0; а – b ≈ 27,4.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте
Тип 2. Единичный выбор
Укажите соседей числа.
Между какими числами расположено иррациональное число 0,1011011…
Математика. 6 класс
Конспект урока
Непериодические десятичные дроби
Перечень рассматриваемых вопросов:
Рациональное число, можно записать в виде конечной или бесконечной периодической десятичной дроби.
Существуют бесконечные непериодические десятичные дроби. Например, дроби 0,010010001…; 17,12345678910…
Бесконечные десятичные дроби называют числами.
Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.
Рациональные и иррациональные числа называются действительными числами.
Теоретический материал для самостоятельного изучения
Рассмотрим положительную бесконечную десятичную дробь 0,1011011101111…
У этой дроби нет группы цифр, являющейся периодом. Эта дробь непериодическая.
Примеры бесконечных непериодических дробей
Поставив перед положительной дробью знак «–», получим отрицательную дробь.
является отрицательной бесконечной непериодической дробью.
Обнаружены новые числа, которые раньше не встречались. Эти новые для вас числа называют иррациональными.
Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.
Рациональные и иррациональные числа называются действительными числами.
Любое действительное число представляется в виде бесконечной десятичной дроби.
Если число – рациональное, то дробь – периодическая, а если иррациональное, то дробь – непериодическая.
Считается, что иррациональные числа были открыты в Древней Греции приблизительно за 400 лет до нашей эры. Самое знаменитое иррациональное число пи обозначается греческой буквой – π и приближенно равно 3,141592653589793238462643.
Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют «День числа пи». В этот день даже проводятся соревнования по запоминанию десятичных знаков этого числа.
Что мы знаем о числах?
Рассмотрим, как выполняются действия с действительными числами. На практике бесконечные десятичные дроби складывают, вычитают, умножают и делят приближенно.
Пример 1. Сравните: 0,(23) и 0,1234…
Чтобы сравнить дроби надо уравнять количество десятичных знаков и затем сравнить.
Пример 2. Найдем приближенную сумму и разность чисел а и b, округлив их с точностью до одной десятой, если а = 23,(18), b = – 4,23(75).
Решение: округляя эти числа с точностью до одной десятой, находим, что а ≈ 23,2 и b = – 4,2. Тогда а + b ≈ 19,0; а – b ≈ 27,4.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте
Тип 2. Единичный выбор
Укажите соседей числа.
Между какими числами расположено иррациональное число 0,1011011…
Десятичные дроби: определения, запись, примеры, действия с десятичными дробями
Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Десятичные дроби представляют собой дробные числа в десятичной записи.
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
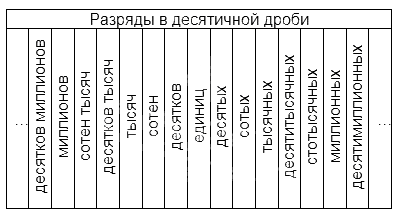
Что такое разряды в десятичных дробях
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:
Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.
Что такое конечные десятичные дроби
Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:
Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Основные действия с десятичными дробями
С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.
Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.
Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.
Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.
Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.
Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.
Положение десятичных дробей на оси координат
Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.
Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.
Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.
Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.
Бесконечные периодические и непериодические десятичные дроби
Содержание
Бесконечные периодические и непериодические десятичные дроби
В десятичной записи конечной десятичной дроби после запятой стоит конечное число десятичных знаков.
В десятичной записи бесконечной десятичной дроби после запятой стоит бесконечное число десятичных знаков.
Бесконечные десятичные дроби бывают периодическими и непериодическими.
Повторяющаяся группа цифр называется периодом бесконечной периодической десятичной дроби.
Для обозначения периода десятичной дроби используют круглые скобки.
Бесконечная десятичная дробь, не являющаяся периодической, называется непериодической.
Алгоритм обращения бесконечной периодической десятичной дроби в простую дробь
Разберем алгоритм обращения бесконечной периодической десятичной дроби в простую дробь на примере решений следующих задач.
ОТВЕТ : 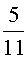
ОТВЕТ : 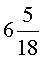
Демонстрационные варианты ЕГЭ и ОГЭ
С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Наши учебные пособия для школьников
При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.