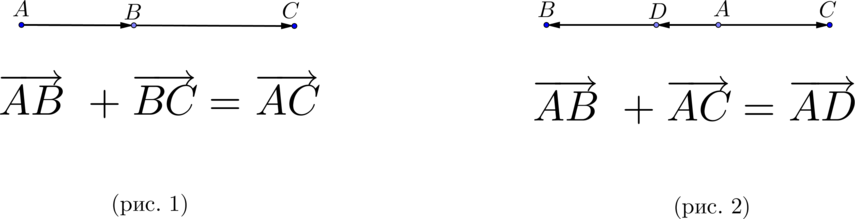Что значит ненулевой коллинеарный вектор

Коллинеарные вектора

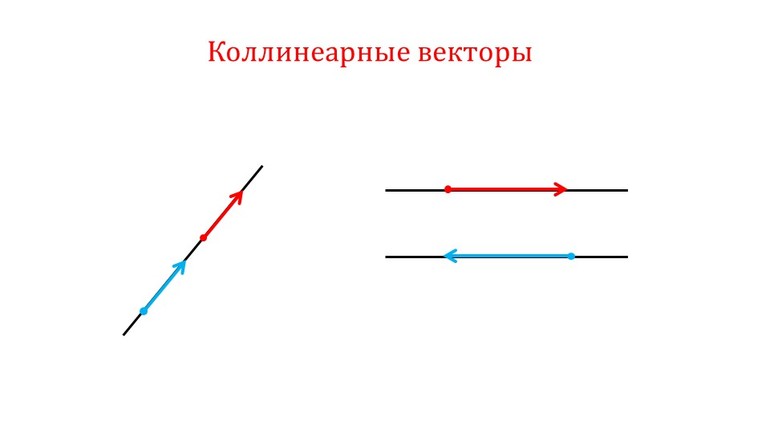
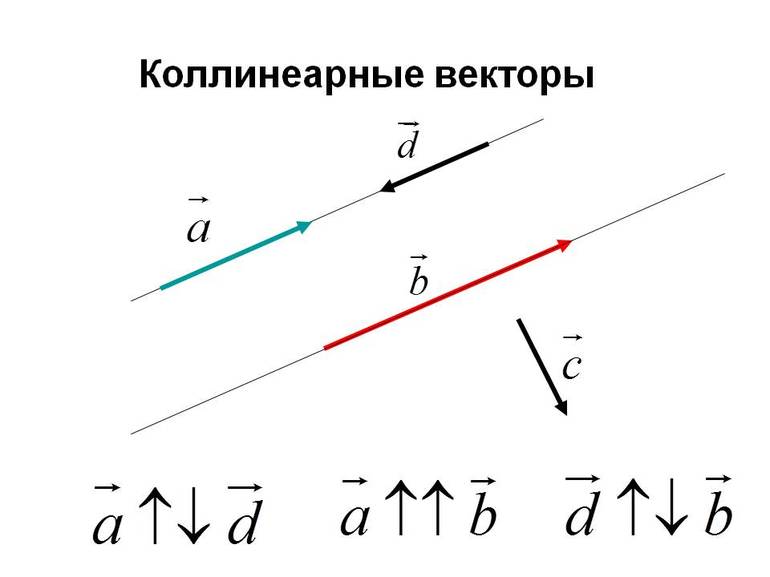
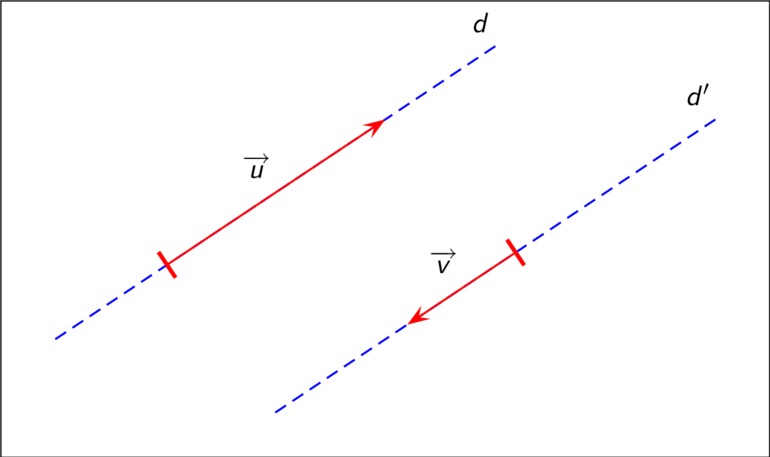
Два вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется, синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Содержание

Обозначения

Свойства коллинеарности

Пусть 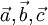— векторы пространства . Тогда верны следующие утверждения:

Другие объекты

Выше описанные критерии коллинеарности позволяют определить это понятие для векторов, понимаемых не в геометрическом смысле (а, например, как элементы произвольного линейного пространства).

Иногда коллинеарными называют те точки (или другие объекты), которые лежат на (принадлежат) одной прямой.

См. также

Полезное

Смотреть что такое «Коллинеарные вектора» в других словарях:

Коллинеарные векторы — Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Допустим, но не рекомендуется, синоним «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или… … Википедия

КОЛЛИНЕАРНЫЕ ВЕКТОРЫ — векторы, лежащие на одной прямой или на параллельных прямых. Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны. Нулевой вектор коллинеарен всякому вектору. Аналогично,… … Математическая энциклопедия

Коллинеарность — Два коллинеарных противоположно направленных вектора Два ненулевых (не равных 0) вектора называются … Википедия

Вектор — направленный отрезок прямой, или отрезок, один из концов которого называется началом вектора, а другой его концом. Различают: 1) коллинеарные векторы, лежащие на одной прямой или на параллельных прямых; 2) компланарные векторы, лежащие в одной… … Начала современного естествознания

Источник

Коллинеарные векторы

В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.

Условия коллинеарности векторов

Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.

Два вектора коллинеарны, если выполняется одно из условий ниже:

2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.

3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).

Примеры задач

Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.

Задание 2
Выясним, при каком значении n векторы и коллинеарны.

Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.

Источник

Общие сведения

Вектором называют направленный отрезок, который имеет начало и конец. Обозначают его либо большими буквами, либо маленькими, например, АБ или a. Над буквой ставится знак вектора — стрелка. Любой отрезок характеризуется длиной, которую называют модулем. Если начало и конец прямой совпадают, то такой вектор носит название нулевой и обозначается в виде точки. При этом его модуль будет равняться нулю.

Для равенства векторов необходимо выполнение двух условий:

Равные вектора могут быть совмещены параллельным переносом, при этом начало и конец отрезков должны совпадать. Если ограниченные линии не являются равными, но лежат на параллельных прямых, то их называют коллинеарными, то есть, по определению коллинеарных векторов, их направление для определения признака не является важным.

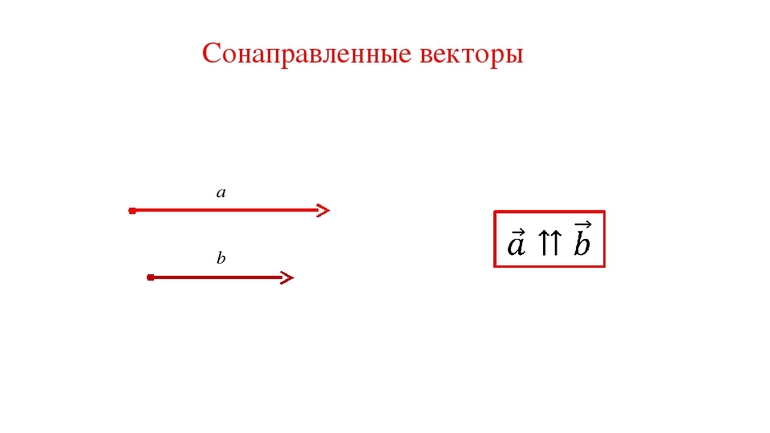
Коллинеарность является одним из признаков сонаправленности, но для выполнения последнего они должны ещё и совпадать по направлению. Наглядным понятием, объясняющим сонаправленность, является прямое движение транспорта или пешехода. Например, если рассматривать две траектории движения как векторы АБ и СД, лежащие на плоскости, при этом их лучи лежат в одной полуплоскости и перпендикулярны её границам, то их можно назвать сонаправленными.

Поэтому параллельные отрезки будут направлены в одну сторону лишь тогда, когда их лучи находятся по одну сторону от прямой, соединяющей их начала. При этом если векторы коллинеарны, но не сонаправлены, то они будут являться противоположными.

С векторами можно выполнять любые простейшие арифметические операции. При сложении используют правила параллелограмма и треугольника. Пусть есть два отрезка, имеющие общее начало. Для того чтобы найти их сумму, необходимо фигуру достроить до параллелограмма. Диагональ этой фигуры и будет искомой величиной. Когда же конец одного отрезка является началом другого, то, соединив свободные точки, можно получить треугольник. Новая прямая и будет являться вектором суммы. Следует отметить, что эти правила равнозначны друг другу. Вычитание отрезков находится аналогично.

Вектор можно и умножить на число, то есть длина отрезка увеличивается на значение множителя. Если в произведении стоит отрицательное число, то характеристика меняет направление.

Критерии коллинеарности

Теорема критерия коллинеарности представляет собой утверждение, которое сообщает, что если есть два не ортогональных отрезка, одинаковых по длине, a и b, то вектор a может быть выражен через формулу a || b = a = y * b. При этом y обозначает любое произвольное число. Есть и обратное утверждение: если вектор b умножить на число и получится отрезок a, то тогда a и b будут коллинеарными.

Эти два правила тождественны и называются критериями коллинеарности. Для их доказательства нужно знать правило арифметических действий с параллельными и перпендикулярными векторами, а также понимать основной базис. Заключается он в том, что если имеются три отрезка a, b и c, при этом верной является следующая комбинация a || b и a || c, то справедливо утверждать, что b || c.

Для того чтобы доказать свойство a || b = a = y * b, нужно воспользоваться определением коллинеарности. Из него следует, что если a || b, то отрезки могут быть сонаправлены или противоположно направлены. Таким образом, необходимо проверить утверждение для двух случаев:

Если предположения окажутся верными, то можно будет сделать вывод о справедливости записи для других случаев. То есть к любым параллельным отрезкам можно применить равенство a = u * b. Этот критерий занимает важное место в геометрии наряду со свойствами перпендикулярности (ортогональности) прямых.

Сонаправленные вектора

Пусть a и b однонаправленные. Введём число y, равное отношению a на b. Так как длина вектора может быть только положительной, то и y = a /b > 0. Состояние вектора, когда он нулевой, является частным случаем и его можно не рассматривать, так как при этом получится равенство 0 = 0. Если длину b умножить на число, то получится новый вектор. Пусть это будет отрезок c, то есть с = y * b. Учитывая свойство коллинеарности, можно утверждать, что между c и b останется параллельность.

По условию известно, что a || b. Исходя из транзитивности отрезков, можно заключить, что и c || b. Теперь необходимо установить их направление. Изначально a и b направлены в одну сторону. Ведённый множитель больше нуля. Это значит, что после умножения направление вектора не изменится, то есть c будет иметь то же направление что и b. Тогда получается, что a || b и c || b. Отсюда следует, что a || с.

Длина вектора c равняется |c| = |u| * |b|. Вместо u можно подставить a / b. В итоге получится |a| * |b| / |b| = |a|. Таким образом, два условия выполняются, и можно утверждать, что с = a. Получается, что для двух любых однонаправленных векторов будет выполняться правило a = u * b.

Противоположные отрезки

Использование онлайн-калькулятора

Решение простых заданий из школьного курса обычно не вызывает сложностей. Но на практике приходится сталкиваться со сложными выражениями. Для их вычисления нужно проявить усидчивость и при этом быть предельно внимательным. Кроме этого, расчёт занимает довольно много времени, а любая, казалось бы, незначительная оплошность, приведёт к неправильному решению.

Поэтому условие коллинеарности векторов удобно проверять на так называемых онлайн-калькуляторах. Это обычно мощные сервисы, основная деятельность которых заключается в предоставлении услуг по автоматизации вычислений. Среди них попадаются и сайты, умеющие вычислять и вектора.

Для того чтобы выполнить на них математические операции, необходимо иметь доступ к интернету и установленный веб-обозреватель. Всё, что требуется от пользователя, это просто зайти на сайт и выбрать раздел, связанный с операциями над векторами. Затем в предложенную форму вести условие задания и запустить расчёт нажатием одной кнопки.

Из множества онлайн-расчётчиков, доступных в секторе рунета, можно выделить следующие:

Все указанные сервисы предоставляют доступ к услугам бесплатно и без регистрации. Воспользовавшись онлайн-калькуляторами, даже слабо подготовленный пользователь научится самостоятельно определять коллинеарность. Такие расчётчики будут полезны и учащимся, и инженерам.

Источник

Линейная зависимость системы векторов. Коллинеарные векторы

В данной статье мы расскажем:

Коллинеарные векторы

Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Примеры задач на исследование коллинеарности векторов

Исследуем векторы а = ( 1 ; 3 ) и b = ( 2 ; 1 ) на коллинеарность.

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.

Ответ: a | | b

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

Критерии линейной зависимости и линейной независимости систем векторов

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Делим обе части равенства на ненулевой коэффициент:

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

Переносим вектор e k в правую часть этого равенства:

Свойства линейно зависимых векторов

Примеры решения задач на линейную зависимость или линейную независимость векторов

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записываем векторное уравнение в виде линейного:

Решаем эту систему при помощи метода Гаусса:

Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

Источник

Векторы. Начальные сведения

Определения

Если длина вектора равна нулю (совпадают начало и конец), то такой вектор называют нулевым.

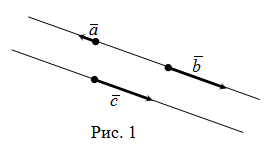
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( \(\overrightarrow a, \overrightarrow b\) и \(\overrightarrow c\) ).

В противном случае векторы называются неколлинеарными (например, \(\overrightarrow a\) и \(\overrightarrow d\) ).

Векторы называются равными, если они сонаправлены и их длины равны.

Правила сложения коллинеарных векторов:

\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

Правила сложения неколлинеарных векторов \(\overrightarrow \) и \(\overrightarrow\) :

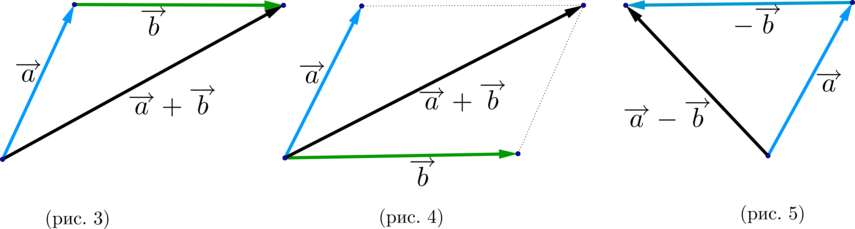
\(\blacktriangleright\) Правило треугольника (рис. 3).

\(\blacktriangleright\) Правило параллелограмма (рис. 4).

Определение

Вектор \(\overrightarrow <-b>\) – это вектор, противоположно направленный с вектором \(\overrightarrow \) и совпадающий с ним по длине.

Свойства сложения векторов

Замечание

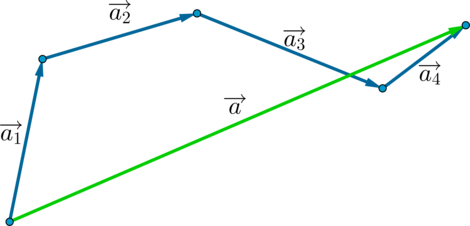
Для того, чтобы сложить несколько вектором, можно отложить их последовательно: каждый следующий от конца предыдущего. Тогда суммой этих векторов будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего: \[\overrightarrow +\overrightarrow +\overrightarrow + \overrightarrow =\overrightarrow \]

Определение

Свойства произведения вектора на число

1. Сочетательный закон: \(k(\lambda\overrightarrow )=(k\lambda)\overrightarrow \) ;

Теорема

Источник