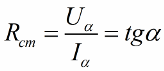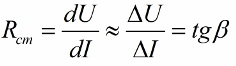Что значит нелинейный контейнер
Линейные и нелинейные элементы электрической цепи
Те элементы электрической цепи, для которых зависимость тока от напряжения I(U) или напряжения от тока U(I), а также сопротивление R, постоянны, называются линейными элементами электрической цепи. Соответственно и цепь, состоящая из таких элементов, именуется линейной электрической цепью.
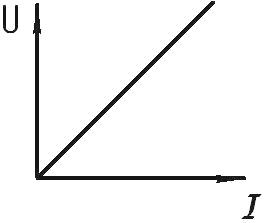
Для линейных элементов характерна линейная симметричная вольт-амперная характеристика (ВАХ), выглядящая как прямая линия, проходящая через начало координат под определенным углом к координатным осям. Это свидетельствует о том, что для линейных элементов и для линейных электрических цепей закон Ома строго выполняется.
Яркий пример линейного элемента — проволочный резистор. Ток через такой резистор в определенном диапазоне рабочих напряжений линейно зависит от величины сопротивления и от приложенного к резистору напряжения.
Характеристика проводника (вольтамперная характеристика) — зависимость между напряжением, подводимым к проводнику, и силой тока в нем (обычно выраженная в виде графика).
Для металлического проводника, например, сила тока в нем пропорциональна приложенному напряжению, и поэтому характеристика представляет собой прямую линию. Чем круче идет прямая, тем меньше сопротивление проводника. Однако некоторые проводники, в которых ток не пропорционален приложенному напряжению (например, газоразрядные лампы), имеют более сложную, не прямолинейную вольтамперную характеристику.
Если же для элемента электрической цепи зависимость тока от напряжения или напряжения от тока, а также сопротивление R, непостоянны, то есть изменяются в зависимости от тока или от приложенного напряжения, то такие элементы называются нелинейными, и соответственно электрическая цепь, содержащая минимум один нелинейный элемент, окажется нелинейной электрической цепью.
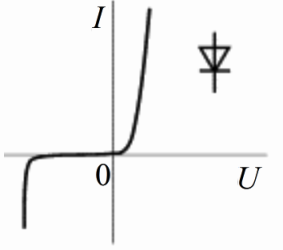
Вольт-амперная характеристика нелинейного элемента уже не является прямой линией на графике, она непрямолинейна и часто несимметрична, как например у полупроводникового диода. Для нелинейных элементов электрической цепи закон Ома не выполняется.
В данном контексте речь может идти не только о лампе накаливания или о полупроводниковом приборе, но и о нелинейных индуктивностях и емкостях, у которых магнитный поток Ф и заряд q нелинейно связаны с током катушки или с напряжением между обкладками конденсатора. Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.
Пример нелинейного элемента — лампа накаливания. С ростом тока через нить накаливания лампы, ее температура увеличивается и сопротивление возрастает, а значит оно непостоянно, и следовательно данный элемент электрической цепи нелинеен.
Такой подход делает возможным простейший анализ и расчет простых нелинейных цепей.
На рисунке выше показана ВАХ типичного диода. Она располагается в первом и в третьем квадрантах координатной плоскости, это говорит нам о том, что при положительном или отрицательном приложенном к p-n-переходу диода напряжении (в том или ином направлении) будет иметь место прямое либо обратное смещение p-n-перехода диода. С ростом напряжения на диоде в любом из направлений ток сначала слабо увеличивается, а после резко возрастает. По этой причине диод относится к неуправляемым нелинейным двухполюсникам.
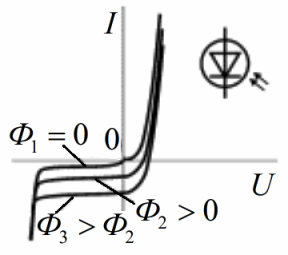
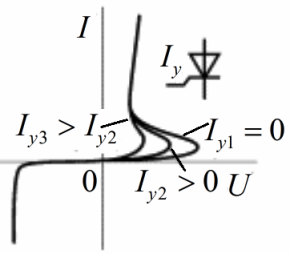
Это ВАХ тиристора, здесь видна ее явная зависимость от величины тока управляющего электрода. В первом квадранте — рабочий участок тиристора. В третьем квадранте начало ВАХ — малый ток и большое приложенное напряжение (в запертом состоянии сопротивление тиристора очень велико). В первом квадранте ток велик, падение напряжения мало — тиристор в данный момент открыт.
Момент перехода из закрытого — в открытое состояние наступает тогда, когда на управляющий электрод подан определенный ток. Переключение из открытого состояния — в закрытое происходит при снижении тока через тиристор. Таким образом, тиристор — это управляемый нелинейный трехполюсник (как и транзистор, у которого ток коллектора зависит от тока базы).
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Линейные и нелинейные электрические цепи
Электрической цепью является совокупность элементов и устройств, соединенных проводами и предназначенных для производства, передачи и распределения электрической энергии.
Происходящие в ней электромагнитные процессы рассчитываются при помощи таких параметров, как сила тока, электродвижущая сила, напряжение, сопротивление, емкость и индуктивность.
Различают линейные и нелинейные электрические цепи.
Линейные электрические цепи
При независимом от напряжения и силы тока сопротивлении, линейную зависимость между этими параметрами показывает закон Ома:
Вольтамперная характеристика в данном случае будет представлена прямой линией.
В том случае, когда индуктивность соленоида не зависима от силы тока, что проходит через нее, потокосцепление ψ будет прямо пропорционально данной силе тока:
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Но линейность вышеуказанных величин – это понятие условное, так как в реальных электрических цепях перечисленные элементы будут нелинейные. К примеру, при протекании электрического тока по резистору, он греется, вследствие чего увеличивается его сопротивление.
Так как в обычном рабочем режиме такие изменения незначительны, ими попросту пренебрегают, считая данные элементы линейными.
Транзисторы, которые функционируют в режиме, когда их вольтамперные характеристики представлены прямыми линиями, условно тоже приравниваются к линейным.
Значит, линейные электрические цепи – это цепи, что включают только линейные элементы. Для их описания используют линейные уравнения.
Нелинейные электрические цепи
Расчет нелинейных цепей
Рассчитать нелинейные элементы цепи не так просто, поэтому обычно стремятся выбрать часть цепи, приравниваемую к линейной. В таком случае с допускаемой точностью элемент рассматривают как линейный. Если нет возможности считать элемент линейным, то используют специальные методы расчета нелинейных цепей:
Не нашли что искали?
Просто напиши и мы поможем
Суть графического метода заключается в построении параметрических характеристик элементов (вольтамперной, кулонамперной или веберамперной) с их дальнейшим графическим преобразованием для того, чтобы получить искомую характеристику всей цепи или отдельной ее части. Данный метод достаточно точный, простой и удобный для наглядности. Чаще всего им пользуются при небольшом числе нелинейных элементов в цепи, так как построение графиков требует особой аккуратности и точности.
Суть метода аппроксимации заключается в том, что полученные экспериментальным путем характеристики нелинейных элементов замещаются на математические выражения. При этом используют аналитическую или кусочно-линейную аппроксимацию. При методе аналитической аппроксимации характеристика нелинейного элемента замещается математической функцией, а при кусочно-линейной – набором прямолинейных отрезков.
Точность аналитической аппроксимации зависит от верности выбора функции аппроксимации и подбора нужных коэффициентов. Преимущество кусочно-линейной аппроксимации заключается в простоте использования и наличии возможности приравнивать элемент к линейному.
Кроме того, при небольшом диапазоне вариации сигнала, когда из-за его трансформаций он приравнивается к линейному (режим незначительного сигнала), нелинейный элемент с допустимой точностью заменяют эквивалентно на линейный активный двухполюсник:
где \(R_д\) – дифференциальное значение сопротивления нелинейного элемента на приравненном к линейному участке.
Digitrode
цифровая электроника вычислительная техника встраиваемые системы
В чем разница между линейными и нелинейными цепями
Чем отличаются линейные цепи от нелинейных
В электротехнике по одной из классификаций электрические цепи делятся на два вида – линейные и нелинейные. Для новичков эти понятия немного запутанны и не совсем ясно с первого взгляда, какую цепь относить к линейной, а какую к нелинейной.
Линейные цепи
Если говорить простыми словами, линейная схема представляет собой электрическую цепь, в которой параметры схемы (сопротивление, индуктивность, емкость, сигналы, частота и т. д.) являются постоянными. Другими словами, схема, параметры которой не изменяются относительно тока и напряжения, называется линейной цепью.
По сути, слово «линейный» буквально означает «по прямой линиии». Как следует из названия, линейная схема предусматривает линейные зависимости между током и напряжением, что означает, что ток, протекающий через цепь, прямо пропорционален приложенному напряжению. Если мы увеличим приложенное напряжение, то ток, протекающий по цепи, также увеличится, и наоборот. Если мы проведем характеристическую кривую выходного сигнала зависимости тока от напряжения, она будет выглядеть как прямая линия, как показано на приведенном далее рисунке.
Если обратиться к Закону Ома, то можно сказать, что если приложенное напряжение повышается, то ток повышается таким же образом в случае, если сопротивление постоянно. Другими словами в линейной цепи выходной сигнал схемы прямо пропорционален входу. Например, в схеме, в которой применяемое синусоидальное напряжение, имеющее частоту «f», выход (ток через компонент или напряжение между двумя точками) этой схемы также является синусоидальным с частотой «f». К классическим линейным цепям относят резистивные цепи, индуктивные цепи и емкостные цепи.
Нелинейные цепи
Нелинейная цепь представляет собой электрическую схему, параметры которой изменяются относительно тока и напряжения. Другими словами, электрическая цепь, в которой параметры схемы (сопротивление, индуктивность, емкость, сигналы, частота и т. д.) не являются постоянными, называется нелинейной цепью.
В нелинейных цепях могут присутствовать такие активные компоненты как диод, транзистор, тиристор, трансформатор и т.п. Ниже показана вольт-амперная характеристика нелинейной цепи с использованием диода.
Расчет нелинейной цепи немного сложнее, чем линейных схем. Линейная цепь может быть рассчитана с помощью простых методов и научного калькулятора. При решении нелинейных схем требуется много данных и информации. Но в наши дни благодаря технологическим изменениям и прогрессу мы можем легко имитировать и анализировать линейные и нелинейные схемы с помощью инструментов моделирования схем, таких как PSpice, MATLAB, Multisim и т. д.
Нелинейные электрические цепи
Назначение нелинейных элементов в электрических цепях
Вольт-амперные характеристики нелинейных элементов
Электрические свойства нелинейных элементов представляют вольт-амперными характеристиками I(U) экспериментально полученными графиками, отображающими зависимость тока от напряжения, для которых иногда составляют приближенную, удобную для расчетов эмпирическую формулу.
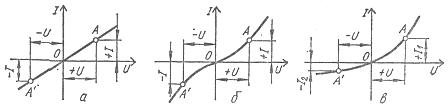
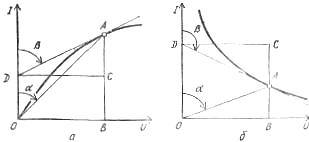
У линейных элементов электрическое сопротивление постоянно, поэтому вольт-амперная характеристика их является прямой линией, проходящей через начало координат (рис. 1, а).
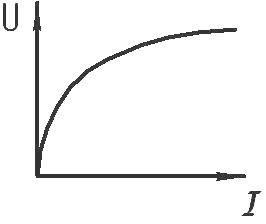
Вольт-амперные характеристики нелинейных имеют различную форму и разделяются на симметричные и несимметричные относительно осей координат (рис. 1, б, в).
У нелинейных элементов с симметричной вольт-амперной характеристикой, или у симметричных, элементов, перемена направления напряжения не вызывает изменения значения тока (рис. 1, б), а у нелинейных элементов с несимметричной вольт-амперной характеристикой, или у несимметричных элементов, при одном и том же абсолютном значении напряжения, направленного в противоположные стороны, токи разные (рис. 1, в). Поэтому нелинейные симметричные элементы применяют в цепях постоянного и переменного тока, а нелинейные несимметричные элементы, как правило, в цепях переменного тока для преобразования переменного тока в ток постоянного направления.
Характеристики нелинейных элементов
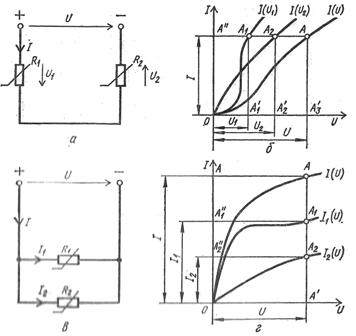
Для каждого нелинейного элемента различают статическое сопротивление, соответствующее данной точке вольт-амперной характеристики, например, точке А:
R ст = U/I = muOB / miBA = mr tgα
и дифференциальное сопротивление, которое для. той же точки А определяется по формуле:
или относительной проводимостью:
У линейных элементов параметры Kr и Kg равны единице, а у нелинейных элементов отличаются от нее, причем чем больше они отличаются от единицы, тем больше проявляется нелинейность электрической цепи.
Аналитический метод расчета нелинейных электрических цепей основан на представлении вольт-амперных характеристик нелинейных элементов уравнениями соответствующих математических функций, позволяющих составить необходимые уравнения состояния электрических цепей. Поскольку решение таких нелинейных уравнений часто вызывает значительные трудности, аналитический метод расчета нелинейных цепей удобен, когда рабочие участки вольт-амперных характеристик нелинейных элементов могут быть спрямлены. Это позволяет описать электрическое состояние цепи линейными уравнениями, не вызывающими затруднения при их решении.
Просто о нелинейном анализе методом конечных элементов. На примере кронштейна
Привет, Хабр! Цель написания этой статьи – как можно более понятно представить приемы конечно-элементного моделирования на примере такой непростой темы, как нелинейный анализ. Я более семи лет проработал в отделе динамической прочности АО «ВПК «НПО машиностроения», где занимался расчетно-экспериментальным сопровождением изделий ракетно-космической отрасли. Также около трех лет помогал строительным и нефтяным компаниям закрывать их самые сложные расчетные проблемы. Пришло время поделиться опытом.
Продакт-менеджер по направлению Femap АО «Нанософт» Филипп Титаренко
Введение, или Зачем и про что эта статья
Далеко не все инженеры умеют решать задачи нелинейного анализа. А многих, даже из числа тех, кто специализируется на расчетах в программах конечно-элементного анализа, словосочетание «нелинейный анализ» вводит в заблуждение или же вовсе пугает. Тем, кто мимоходом пробовал решать такие задачи, вспоминаются окна с большим количеством настроек и какие-то графики, которые куда-то движутся и при этом что-то «не сходится» (рис. 1). Однако не только научные задачи, но и современные инженерные нормы и стандарты зачастую требуют учитывать нелинейность в расчетных моделях. Причем эти требования существуют не только в космической, авиационной, машиностроительной отраслях. Так, например, свод правил СП 385.1325800.2018 «Защита зданий и сооружений от прогрессирующего обрушения» при проведении расчетов требует учитывать геометрическую и физическую (пластичность, ползучесть и др.) нелинейности.

Рисунок 1
Статистика на сегодняшний день такова, что около 90% расчетов приходится на линейный анализ. С точки зрения экономики, линейный анализ – это быстро, просто и дешево. Но если вам необходимо рассчитать отклик на воздействие ударов, учесть инерционные эффекты, проследить изменение температурных или других параметров во времени, учесть наличие поверхностей контакта, геометрические нелинейности или сложные механизмы поведения материалов, без нелинейного анализа и без умения правильно настроить решатель вам не обойтись. Основные виды нелинейности – физическая геометрическая и обусловленная наличием поверхностей контакта.
В Рунете (да и в глобальной сети) на тему нелинейного анализа методом конечных элементов есть два условных типа образовательных материалов: 1) не слишком длинные инструкции, куда и в какой последовательности нажать в вашей САПР, чтобы рассчитать ваши «балку, нагрев, кронштейн, течение…», либо 2) толстые институтские учебники/научные работы или многостраничные руководства пользователя, которые можно и нужно долго изучать… но в ближайшие дни и недели вряд ли получится что-то посчитать самостоятельно.
Данная статья – это попытка автора на конкретном примере в конкретной САПР проиллюстрировать алгоритм проведения нелинейного статического анализа «с нуля» и до анализа решения, при этом предложив некоторые объяснения теоретическим основам, связанным с настройками решателя.
Задачу мы будем решать в пре-постпроцессоре Femap с решателем NX Nastran, еще с середины 70-х годов прошлого века многократно доказавшим свои надежность, точность и скорость. Я пользуюсь Femap 2020.2, но в целом алгоритм решения такого рода задач идентичен не только в предыдущих версиях Femap, но и в других КЭ расчетных комплексах.
На чем будем тренироваться? Нелинейный статический анализ
Нет, тренироваться, в отличие от героя старой кинокомедии (рис. 2), будем не на кошках.

Рисунок 2
Нам предстоит рассчитать Г-образный кронштейн за пределом текучести стали. Реальным прототипом кронштейна может быть альпинистский шлямбур, кронштейн на МКС или элемент навесного вентилируемого фасада. Я выбрал его потому что, с одной стороны, не хотел брать готовую модель, а с другой – хорошо было бы не тратить много времени читателя на процесс создания геометрии. С точки зрения модели все будет максимально просто, больше внимания я уделю теории и настройкам решателя. При таком подходе у читателя будет возможность самостоятельно повторить весь процесс – от создания модели до ее численного анализа. И даже провести натурный эксперимент.
В процессе подготовки статьи я обнаружил у себя дома подобный, но перфорированный кронштейн (рис. 3), ранее выведенный мною плоскогубцами за пределы текучести – правда, при других граничных условиях закрепления. И в других целях – не научно-экспериментальных, а в бытовых…

Рисунок 3
Но при желании вы всегда сможете верифицировать свой численный эксперимент: такие кронштейны есть во всех строительных магазинах.
Немного теории: отличия линейного и нелинейного анализа
Для практики решения инженерных задач с точки зрения внутренних расчетных алгоритмов важно осознавать, что в нелинейном анализе нагрузки прикладываются постепенно и фактически решатель последовательно решает множество задач. При линейном статическом анализе всегда делается лишь один шаг: от начального состояния к конечному. При решении нелинейной задачи все заданные нагрузки будут приложены к телу не сразу.
Исходными данными для каждого последующего шага в нелинейном анализе является состояние модели на предыдущем шаге. Причем на каждом шаге внутренние и внешние силы (энергетические параметры) должны быть уравновешены с учетом некоторой погрешности (рис. 4). Величину допустимой погрешности определяет критерий сходимости (Convergence Tolerances). Обычно этот критерий задается в процентах от приложенной нагрузки, где под нагрузкой понимаются все приложенные к модели внешние силы или, в случае нагружения перемещением, – силы реакции. Обилие настроек объясняется сложностью расчетных алгоритмов, сопутствующих нелинейному анализу. Типовое значение критерия сходимости по силам находится в диапазоне от 0,1 до 1% приложенной нагрузки. В поиске сходимости на шаге решения программа может выполнить множество итераций. По этим причинам решение нелинейных задач занимает намного больше машинного времени, чем решение линейных статических задач. Важно осознавать, что многошагового подхода могут по разным причинам (типам нелинейностей) требовать задачи, результат решения которых не зависит от времени.

Рисунок 4
Самый простой пример, на котором можно понять это утверждение, – нагружение упруго-пластичной конструкции нагрузкой, при которой напряжение превысит предел текучести. Решатель заранее «не знает», при какой нагрузке напряжение в отдельных узлах модели превысит этот предел и, следовательно, принципиально изменятся параметры уравнений, описывающих напряженно-деформированное состояние тела. При этом на каждом шаге приращения силы нужно учитывать изменение зоны пластической деформации. Поэтому решение проходит множество шагов приращения нагрузки, а шаги в свою очередь при необходимости выполняются за определенное количество итераций. Вычисления матрицы жесткости могут повторно осуществляться на каждом шаге решения. Частота пересчета матрицы жесткости задается пользователем. Пластичность – это физическая нелинейность.
В связи с «многошаговостью» и «итерационностью» процесса решения рекомендую освоить вкладку Nonlinear History (Нелинейная хронология решения), на которую можно перейти, запустив решатель. В ней вы сможете по графику в режиме реального времени отслеживать количество выполненных итераций и уровень достигнутой нагрузки (Load Factor). По этому графику можно анализировать скорость сходимости решения. Если что-то пошло не так, то решатель прервет процесс решения и выдаст сообщение, что решение не сходится.
Линейный анализ может использоваться только для анализа моделей с линейными материалами при условии, что нелинейностей других видов нет. Линейные материалы могут быть изотропными, ортотропными или анизотропными. Если материал в модели имеет нелинейные характеристики «напряжение – деформации» под заданной нагрузкой, должен использоваться нелинейный анализ. В нелинейном анализе могут быть использованы различные типы моделей материалов.
При нелинейном статическом анализе динамические явления, подобные инерционным силам и силам демпфирования, не учитываются. Обработка нелинейного статического решения отличается от обработки линейного статического решения несколькими основными позициями, представленными в табл. 1.
Общей теории на этом достаточно, а о том, как настроить алгоритмы решения глобальной нелинейной системы алгебраических уравнений, порождаемой методом конечных элементов, я напишу ниже, когда мы дойдем до соответствующего места при разборе нашего практического примера с кронштейном. В Femap большая часть этих настроек находится в диалоговом окне Nastran Nonlinear Analysis, куда можно попасть из диалогового окна Analysis Set, установив 10..Nonlinear Static в поле Analysis Type и несколько раз нажав кнопку Next. Но всему свое время.
Приступим к практике: моделирование кронштейна и линейный анализ в Femap с NX Nastran
В командном меню открываем File → Preferences → вкладка Geometry/Model. В настройках Solid Geometry Scale Factor устанавливаем Meters, что соответствует системе СИ измерений физических величин.
Наш Г-образный кронштейн будет состоять из двух квадратных пластин со сторонами длиной 0,1 метра, расположенных в перпендикулярных плоскостях. В командном меню перейдем в Geometry → Surface → Corners и последовательно создадим две квадратные пластины.
1) Координаты вершин для первой пластины: 1) X = 0; Y = 0; Z = 0; 2) X = 0,1; Y = 0; Z = 0; 3) X = 0,1; Y = 0; Z = 0,1; 4) X = 0; Y = 0; Z = 0,1.
2) Для второй: 1) X = 0; Y = 0; Z = 0; 2) X = 0; Y = 0,1; Z = 0; 3) X = 0; Y = 0,1; Z = 0,1; 4) X = 0; Y = 0; Z = 0,1.
Последовательно забив эти точки в диалоговое окно Locate → Enter № Corner of Surface, получим нужную геометрию. Нажатием клавиш Ctrl+A мы можем отобразить нашу геометрию в центре видового экрана в удобном масштабе.
Далее создадим материал наших пластин (Сталь 3) и определим его свойства. Для этого в панели Model Info, расположенной в левой части экрана, раскроем вкладку Model, затем щелкнем правой кнопкой мыши на строке Materials и нажмем New. Откроется диалоговое окно Define Material – ISOTROPIC. В поле Title введем наименование St3. В поле General зададим модуль Юнга (Young’s Modulus), E = 2e11, коэффициент Пуассона (Poisson’s Ratio), nu = 0,3, плотность (Mass Density) = 7850. На вкладку Nonlinear пока переходить не будем. Нажимаем ОК, а затем Cancel.
Создадим тип конечного элемента и укажем его свойства. Для этого во вкладке Model щелкнем правой кнопкой мыши на строке Properties и нажмем New. Откроется диалоговое окно Define Property – Plate Element Type. В поле Title введем наименование Pl0005. Во вкладке Material выберем 1..St3. Затем нажмем кнопку Elem/Property Type и убедимся, что флажок стоит в нужном месте: Plane Elements – Plate. То есть выбран плоский конечный элемент – пластина. Зададим толщину пластины, для этого в поле Thicknesses установим TavgorT1 = 0,005. Нажимаем ОК, а затем Cancel.
Сохраним нашу модель, для чего нажмем File → Save As, выберем путь для сохранения файла и имя файла. Я назову его KronNonlin.
Зададим свойства сетки конечно-элементной модели. Для этого в командном меню нажмем Mesh → Mesh Control → Size On Surface. В диалоговом окне Entity Selection → Select Surface(s) to Set Mesh Size нажмем Select All, чтобы выбрать все поверхности. Нажав ОК, мы попадаем в диалоговое окно Automatic Mesh Sizing. В поле Element Size выставляем значение 0,005 и нажимаем ОК. Теперь характерный размер наших конечных элементов будет равен 5 мм. На линиях модели появились точки, дающие нам информацию о том, какого размера будут элементы после создания конечных элементов.
Теперь создадим конечно-элементную модель. В командном меню нажмем Mesh → Geometry → Surface. В диалоговом окне Entity Selection → Select Surfaces to Mesh нажимаем Select All и ОК. В поле Property установим созданный нами тип КЭ 1..Pl0005, а в поле Mesher – флажок Quad. Нажимаем OK. Конечно-элементная модель создана. Теперь закрепим кронштейн и нагрузим его внешними силами.
Крепить кронштейн мы будем за четыре узла (такое закрепление более всего соответствует креплению заклепками или точечной сварке) по шести степеням свободы, и по линии стыка двух пластин – по трем степеням свободы (оставив возможность вращения вокруг линии).

Рисунок 5
Задаем граничные условия закрепления. Для этого щелкаем правой кнопкой мыши на Constraints, нажимаем New и вводим название Constr. Далее нажимаем правой кнопкой на Constraints Definitions и выбираем закрепление по узлам (Nodes). Выбрав четыре узла, как показано на рис. 5, закрепляем их по шести степеням свободы; нажимаем ОК. В поле Title диалогового окна Create Nodal Constraints/DOF пишем 4nodes и нажимаем на кнопку Fixed, чтобы ограничить перемещение-вращение. Нажимаем ОК. Вновь щелкаем правой кнопкой на Constraint Definitions и выбираем закрепление по линии (Curves). В поле Title диалогового окна Create Constraints on Geometry указываем Line и нажимаем кнопку Pinned – No Translation, чтобы ограничить перемещение, оставив возможность вращения.
Зададим условия нагружения, для чего правой кнопкой мыши щелкнем на Loads – New. Новый Set назовем Vert. Нажимаем правой кнопкой на Load Definitions – Nodal и выбираем четыре узла, к которым будут приложены данные нагрузки. В диалоговом окне Create Loadson Nodal назовем нашу нагрузку Force600. Узловые силы направлены по оси Y в отрицательном направлении. Величина узловой нагрузки FY – минус 600 Ньютон. Таким образом, к каждому из четырех узлов будет приложена нагрузка по 600 Ньютон (то есть 240 кг на все четыре узла).
Далее переходим к настройкам анализа. В командном меню выбираем Model → Analyses. Нажимаем кнопку New, чтобы выбрать тип анализа и решатель. В поле Title вводим Linear. Выбираем Analysis Program – 36..Simcenter Nastran и Analysis Type 1..Static. Затем нажатием на кнопку Analyze запускаем расчет. Решение занимает у меня меньше одной секунды (!). Femap показывает нам окно наблюдений за результатами анализа: Simcenter Nastran Analysis Monitor. Строка Analysis complete 0 означает, что анализ успешно завершен.
В Model Info щелкаем правой кнопкой мыши на Results → All Results → Deform. Теперь мы видим деформированное состояние нашего кронштейна в гиперболизированном виде. На мой взгляд, деформированное состояние визуально чрезмерно преувеличено, поэтому нажмем F6: откроется диалоговое окно View options. Перейдем во вкладку PostProcessing, Deformed Style в поле Scale установим 4%. Теперь визуализация деформированного состояния модели преувеличена меньше. Максимальные перемещения можно посмотреть в левом нижнем углу модели – они составляют 0,0026 м.
Нажмем клавишу F5 и отобразим распределение напряжений по модели. В поле Contour Style установим флажок на Contour, затем нажмем кнопку Deformed and Contour Data. Во вкладке Contour выберем 7033 Plate Top Von Mises Stress, чтобы Femap отобразил напряжения в узлах. Наша модель стала разноцветной, цвета отображают уровень напряженности (рис. 6). В правой части экрана мы видим шкалу, отображающую, какому цвету какой уровень напряжений соответствует. Чтобы скрыть геометрическую исходную модель, нажмем на иконку View Surfaces Toggle. Максимальные напряжения достигают 332,4 МПа, что значительно выше предела текучести 210 МПа для стали Ст3.

Рисунок 6
Итак, напряжения в точках кронштейна значительно выше предела текучести. Линейный анализ не учитывает текучесть-пластичность материалов и связанный с этим явлением эффект перераспределения напряжений, поэтому данное распределение напряжений не соответствует реальности. Переходим к нелинейному анализу.
Практика: нелинейный статический анализ в Femap с NX Nastran
Чтобы перейти от линейной к нелинейной модели, нам нужно выполнить всего пару действий (разбиение, условия закрепления и нагрузки мы не меняем).
Изменим свойства материала, добавив пластические деформации; для этого во вкладке Materials щелкнем правой кнопкой мыши на нашем материале 1… St3 и нажмем Edit. Перейдем на вкладку Nonlinear и в поле Nonlinearity Type выберем Plastic. В поле Yield Criterion выберем 0..von Mises, в поле Initial Yield Stress вводим значение 210 000 000 (то есть 210 МПа). Жмем ОК.
NX Nastran поддерживает следующие критерии пластичности:

Рисунок 7
При необходимости учета эффекта ползучести нужно установить галочку в поле Creep.
В поле Basic устанавливаем количество шагов приращения нагрузки (Increments or Time Steps) и максимальное количество итераций на каждом шаге (Max Iterations / Steps). В случае нелинейного статического анализа Increments or Time Steps отражают уровень нагрузки. На графике Nonlinear History (Нелинейная хронология), иллюстрирующем в реальном времени количество выполненных итераций, уровень нагрузки отложен на вертикальной оси и называется Load Factor. Его величина лежит в диапазоне от 0 до 1. За заданное количество шагов нагрузка меняется от 0 до полной; при этом, если того требуют условия сходимости, в рамках одного шага выполняется несколько итераций. Эти два параметра очень важны, в каждой задаче нужно постараться выбрать «золотую середину» между слишком большим количеством «шагов» и «итераций» и слишком маленьким. Если их слишком мало, то решение не сойдется или будет оказано негативное влияние на точность. Если же их количество окажется чрезмерным, решение будет затрачивать очень много машинных мощностей, времени, и может быть оказано негативное влияние на сходимость. Чтобы исследовать влияние этих параметров, мы прорешаем нашу задачку с кронштейном несколько раз при различных сочетаниях количества «шагов» и «итераций», наблюдая при этом за графиком нелинейной хронологии.
Для нелинейной статической задачи в поле Stiffness Updates можно выбрать один из трех методов (AUTO, ITER, SEMI) обновления матрицы жесткости тела, а также количество итераций (Iteration Before Update), через которое матрица будет обновляться. Если метод выбран неверно, то автоматически будет использоваться 0..Default (по умолчанию). В методе AUTO матрица жесткости обновляется исходя из оценок сходимости разных численных методов (квазиньютоновского, с линейной итерацией, половинного деления) и с выбором того из них, что даст минимальное количество обновлений матрицы жесткости. Метод SEMI подобен методу AUTO, но обновление матрицы жесткости обязательно проводится и на первой итерации после изменения нагрузки, что бывает эффективно для сильно нелинейных процессов. Метод ITER (в нелинейном анализе во времени ему подобен метод TSTEP) проводит обновление матрицы жесткости после указанного в поле Iteration Before Update количества итераций. Метод ITER эффективен для сильно нелинейных процессов, при которых геометрия тела в процессе деформирования резко изменяется (например, при потере устойчивости).
В поле Output Control задаются настройки вывода результатов на промежуточных шагах нагружения (временных шагах, если речь идет об анализе во времени). При проведении статического нелинейного анализа во вкладке Intermediate можно выбрать один из следующих вариантов: 0..Default (по умолчанию), YES (выводить), NO (не выводить), All (выводить на всех шагах). При нелинейном анализе во времени можно задать, через какое количество шагов следует выводить результат.
В поле Convergence Tolerance задаются допуски на удовлетворение условий сходимости для нагрузок (Load), перемещений (Displacement) и внутренней работы (Work). Влияние допуска по сходимости (Convergence Tolerances) на точность и время решения задачи рассмотрим на примере модели, изученной разработчиками Femap с NX Nastran из компании Siemens.
Очень большая нелинейная модель (950 000 DOFs) была тщательно исследована, чтобы определить влияние различных допусков критерия сходимости на время выполнения и точность расчета. В этой модели не было теплопередачи, зазоров или контактов. Результаты исследования показали, что приемлемая точность решения (в сравнении с решением, полученным при очень высоком уровне допуска по сходимости) может быть достигнута как для уровня допуска по сходимости «высокий», так и для уровня «инженерный». Уровень допуска по сходимости «предварительная оценка» дает результат с теми же общими тенденциями, что и более высокие уровни допуска, но ответы недостаточно точны для рабочего проекта. При уменьшении уровня допуска по сходимости расчет происходит значительно быстрее. В табл. 2 можно количественно оценить представленные тенденции.
В поле Solution Strategy Overrides устанавливаются настройки процесса решения глобальной нелинейной системы алгебраических уравнений, порождаемой методом конечных элементов. Для осознанного изменения этих настроек нужно обладать знаниями и опытом – если их недостаточно, лучше оставить установки по умолчанию. Приведу некоторые разъяснения.
Arc-Length Method устанавливает величину временного шага (догрузки) с учетом информации о перемещении узлов тела – его следует использовать, если задача связана с резкой деформацией (потерей устойчивости).
Полный метод Ньютона-Рафсона (Full Newton-Raphson) очень быстро сходится, но нуждается в дополнительном времени на создание дополнительной матрицы для полной матрицы системы алгебраических уравнений на каждой итерации.
Модифицированный метод Ньютона-Рафсона (Modified Newton-Raphson) не нуждается в таком действии, но сходится значительно медленнее, поэтому для его ускорения могут применяться дополнительные процедуры: Line Search (линейного поиска), Quasi-Newton (квазиньютоновского ускорения) и/или Bisection (половинного деления).
Таким образом, мы разобрали основные настройки для нелинейного статического анализа (настройки нелинейного анализа во времени им во многом подобны). Для расчета нашего кронштейна в окне Nastran Nonlinear Analysis установим следующие параметры: в поле Increments or Time Steps – 50, Max Iterations / Step – 5, Stiffness Updates Method – 1..AUTO, Iterations Before Update – 5, Intermediate – 1..YES. Остальные настройки оставим без изменений. Нажимаем ОК и переходим в окно Analysis Set Manager. Чтобы запустить расчет, нажмем кнопку Analyze. Femap автоматически откроет окно Simcenter Nastran Analysis Monitor. Перейдем во вкладку Нелинейная хронология, переставив флажок с log на Nonlinear History (рис. 8).

Рисунок 8
Здесь отображается график, иллюстрирующий в реальном времени количество выполненных итераций и (в случае нашего нелинейного статического анализа) Load Factor, то есть фактор нагрузки от 0 до 1. В правом верхнем углу мы видим информацию о номере текущей итерации. Обращаю внимание, что это не номер шага приращения нагрузки, а именно номер текущей итерации. Каждый шаг приращения нагрузки может содержать в себе несколько итераций – это необходимо для выполнения алгоритмов, реализующих сходимость решения. Если приращение не сходится, это означает, что изменение в нагрузке слишком велико, чтобы перейти к следующему шагу; нагрузка снижается – выполняются дополнительные итерации внутри одного шага.
В окне Model Info откроем вкладку Results → All Results. Двойной щелчок мыши на строчке решений открывает результаты при различных уровнях нагрузки от 0 до 100%. Проанализируем совместно график нелинейной хронологии и напряженно-деформированное состояние кронштейна при различных уровнях нагрузки.
При уровне нагрузки от 0 до 0,62 (Load Factor) напряжения меньше предела текучести 210 МПа, после – начинается пластическая деформация стали кронштейна. Единице 1 соответствует полная приложенная нагрузка – 240 кг на четыре узла. Максимальные напряжения выделены красным цветом – они сконцентрированы возле линии пересечения поверхностей. При уровне нагрузки от 0,62 до 1 зона пластических деформаций растет – максимальные напряжения (в отличие от линейного анализа) не увеличиваются. При факторе нагрузки 0,82 скорость роста кривой уменьшается – это значит, что для удовлетворения условий сходимости на каждый шаг требуется большее количество итераций. Мы смогли достигнуть полной нагрузки 1 – максимальные перемещения составили 0,00283 м. В некоторых случаях (например, если бы мы значительно увеличили нагрузку) геометрия деформированного тела искажается настолько, что при данной стратегии (настройках решателя) сходимости достичь не удастся. Как видим, результаты нелинейного анализа качественно и количественно отличаются от результатов линейного анализа.
Проведем еще три расчета, выставив разные настройки по количеству шагов приращений и итераций (рис. 9). В первом случае были выставлены Increments or Time Steps – 50, Max Iterations / Step – 5.

Рисунок 9
Условия сходимости были соблюдены в 1-м, 2-м и 4-м расчетных случаях. В 3-м расчетном случае фатальная ошибка с пояснением, что решение не сходится, появилась при уровне нагрузки 0,8. Обратим внимание, что во 2-м и 4-м расчетах решение было выполнено успешно (полная нагрузка 1) при значительно меньшем количестве шагов и итераций. Наша модель достаточно проста, и все расчеты были проведены менее чем за 5 секунд. На больших моделях благодаря правильному выбору числа шагов приращения нагрузки и итераций может быть сэкономлено много машинного времени.
Заключение
За рамками этой статьи осталось множество вопросов: многоступенчатое нагружение (применение Case и Subcase), применение нелинейных контактов, нелинейный анализ во времени, действия в случаях, когда решение «разваливается». Но я надеюсь, что основная цель статьи достигнута – у тех читателей, кто не имеет обширного опыта в решении нелинейных задач, теперь есть минимальный набор теоретических знаний и практических образов, чтобы начать работу с нелинейным анализом методом конечных элементов.
Литература
Филипп Титаренко,
продакт-менеджер по направлению Femap
АО «Нанософт»
E-mail: titarenko@nanocad.ru
Уважаемые читатели, приглашаю вас на три интересные и полезные мероприятия, которые состоятся в ближайшее время:
Бесплатную пробную версию Femap с NX Nastran можно скачать здесь.