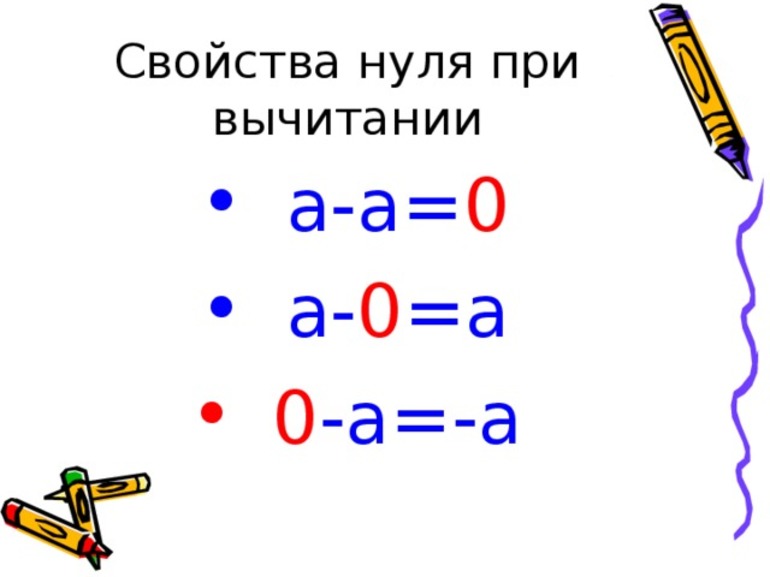
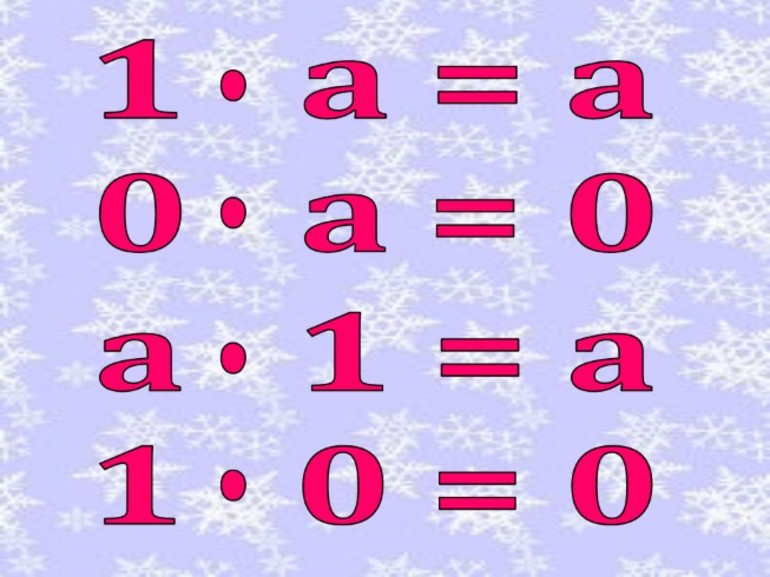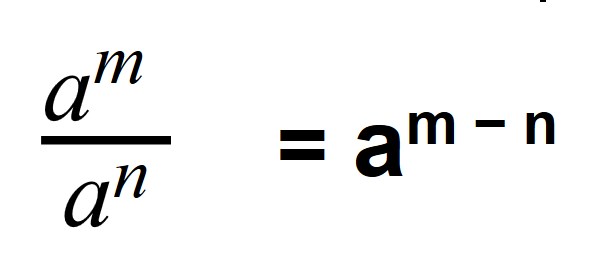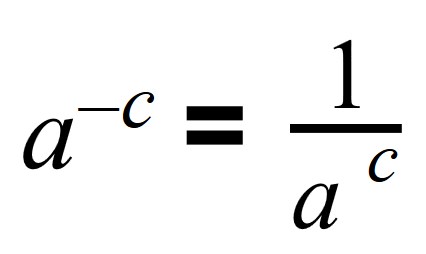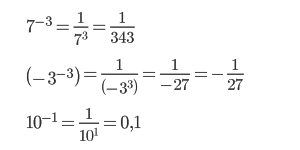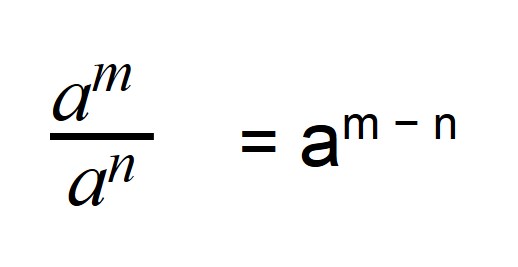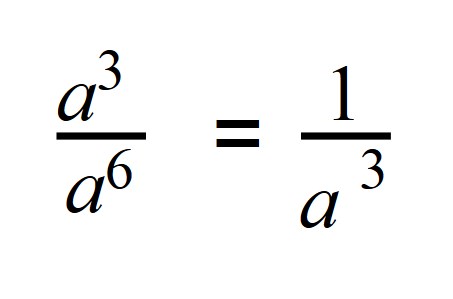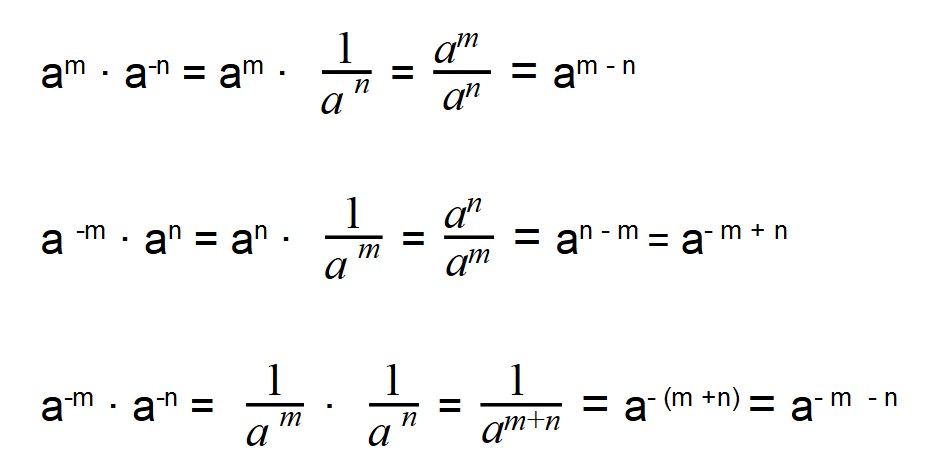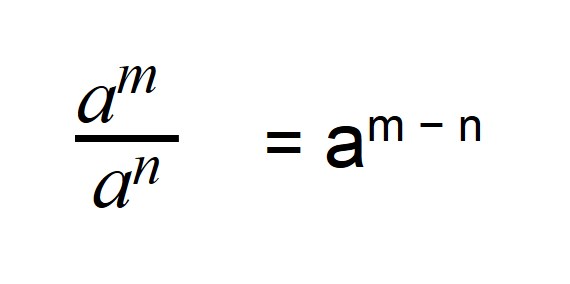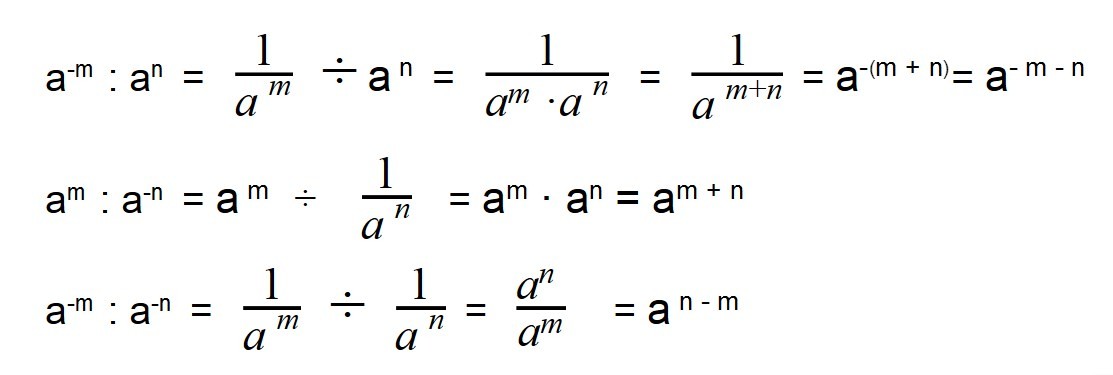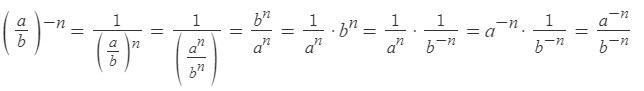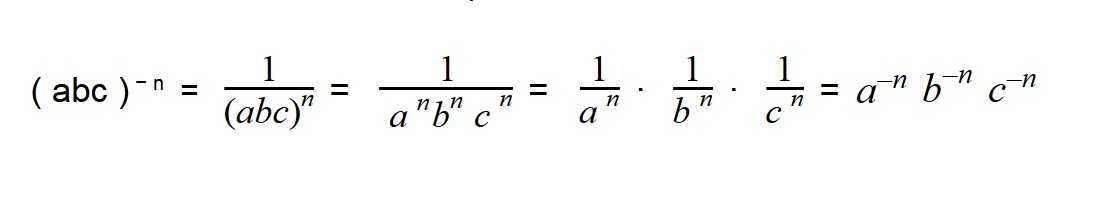Что значит не равное нулю число
Все знают, что на 0 делить нельзя. Но хоть кто-то задавался вопросом «почему?» (не моё)
«Делить на ноль нельзя!» — большинство школьников заучивает это правило наизусть, не задаваясь вопросами. Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему?» А ведь на самом деле очень интересно и важно знать, почему же нельзя.
Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух.
Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись 5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания. Есть только задача — найти подходящее число.
Точно так же обстоит дело с умножением и делением. Запись 8 : 4 можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8.
Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения.
Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение.) А значит, записи 5 : 0 не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя.
Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0=0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д.
Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности», но в арифметике таких случаев не встречается.)
Решение линейных неравенств
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.
Линейные неравенства — это неравенства вида:
где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.
Типы неравенств
Линейные неравенства: свойства и правила
Вспомним свойства числовых неравенств:
Если же а b и c > d, то а + c > b + d.
Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а d, то а – c b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа
Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>
Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.
Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.
Свойства выше помогут нам использовать следующие правила.
Правила линейных неравенств
Решение линейных неравенств
Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.
Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.
Определение 3. Линейные неравенства с одной переменной x выглядят так:
где a и b — действительные числа. А на месте x может быть обычное число.
Равносильные преобразования
Рассмотрим пример: 0 * x + 5 > 0.
Как решаем:
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов это:
Если a ≠ 0, тогда решением будет единственный корень — х₀;
Для этого найдем значения функции в точках на промежутке;
Как решаем:
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
Рассмотрим пример: −5 * x − √3 > 0.
Как решаем
Ответ: (−∞, −√3 : 5) или x
Нулевое число (0)
Определение нулевого числа
Когда на столе 2 яблока и мы берем 2 яблока, мы можем сказать, что на столе нет яблок.
Нулевое число не является положительным и отрицательным числом.
Ноль также является цифрой-заполнителем в других числах (например: 40,103, 170).
Нулевая цифра
При написании чисел нулевая цифра используется в качестве заполнителя.
204 = 2 × 100 + 0 × 10 + 4 × 1
История нулевых номеров
Кто придумал нулевое число?
Современный символ 0 был изобретен в Индии в VI веке, позже использовался персами и арабами, а затем и в Европе.
Символ нуля
В арабской системе счисления используется символ ٠.
Свойства с нулевым числом
x представляет любое число.
| Операция | Правило | пример |
|---|---|---|
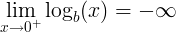 | ||
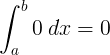 |
Нулевое дополнение
Сложение числа плюс ноль равно числу:
Нулевое вычитание
Вычитание числа минус ноль равно числу:
Умножение на ноль
Умножение числа на ноль равно нулю:
Число деленное на ноль
Деление числа на ноль не определено:
x ÷ 0 не определено
5 ÷ 0 не определено
Ноль делится на число
Деление нуля на число равно нулю:
Число в нулевой степени
Степень числа, возведенного в ноль, равна единице:
Логарифм нуля
Логарифм нуля по основанию b не определен:
Нет числа, с которым мы могли бы поднять основание b до нуля.
Только предел логарифма x по основанию b, когда x сходится к нулю, равен минус бесконечности:
Наборы, содержащие ноль
| Установить | Установить обозначение членства |
|---|---|
| Натуральные числа (неотрицательные) | 0 ∈ ℕ 0 |
| Целые числа | 0 ∈ ℤ |
| Вещественные числа | 0 ∈ ℝ |
| Сложные числа | 0 ∈ ℂ |
| Рациональное число | 0 ∈ ℚ |
Набор четных чисел:
Набор нечетных чисел:
Ноль является членом набора четных чисел:
Есть два определения набора натуральных чисел.
Набор неотрицательных целых чисел:
Набор натуральных чисел:
Ноль является членом набора неотрицательных целых чисел:
Ноль не входит в набор натуральных чисел:
У целых чисел есть три определения:
Набор неотрицательных целых чисел:
Набор натуральных чисел:
Ноль является членом набора целых чисел и набора неотрицательных целых чисел:
Ноль не входит в набор натуральных чисел:
Ноль входит в набор целых чисел:
Является ли ноль рациональным числом?
Ноль можно записать как частное двух целых чисел.
Положительное число определяется как число больше нуля:
Поскольку ноль не больше нуля, это не положительное число.
Число 0 не является простым числом.
Ноль не является положительным числом и имеет бесконечное количество делителей.
История возникновения
Ноль означает ничто, пустоту. Он используется для обозначения пустых разрядов чисел в позиционной системе счисления, а также в десятичных дробях до и после запятой. Вокруг этой цифры всегда велось много споров. Использовать ноль начали еще в древности, о чем свидетельствуют трактаты вавилонян и надписи майя.
Но повсеместно применять в вычислениях его начали лишь спустя несколько тысячелетий. Это произошло в Индии. Нулю там придавали не только математический, но и философский смысл. Он означает отсутствие всего, а его форма соответствовала кругу жизни.
Индусы использовали 0 как любое другое число. Его складывали, вычитали, на него умножали. С делением на 0 возникла проблема, но благодаря ей в дальнейшем возникла другая область математики — математический анализ. Идею использования нуля подхватили исламские ученые на Ближнем Востоке и внесли его в арабскую систему счисления.
В Европе до Крестовых походов применялась Римская система счисления. Это непозиционная система, и ноль в ней отсутствует. Делать расчеты в ней очень тяжело. Для вычислений использовали специальные разграфленные таблицы — абаки. Расчеты с их применением производились часами, в то время как сегодня любой школьник сможет легко получить результат, например, перемножая или складывая числа в столбик.
Во времена первых Крестовых походов арабские цифры вместе с нолем и позиционной системой счисления пришли в Европу. К этим новшествам сначала отнеслись с большим недоверием. Во Флоренции даже был издан закон о запрещении использования арабских цифр вместе с нулем.
Считалось, что они поощряют мошенничество: 0 легко переделать на цифру 9 или приписать в конце счета, чтобы величина долга возросла многократно. Лишь в XV веке, когда началось развитие в сфере математики и механики, люди оценили преимущество нуля и арабских цифр и стали использовать их повсеместно.
Сложение, умножение, степень
В математике используется несколько действий. Они следующие:
Сложение с нулем обычно вопросов не вызывает. Если к любому числу добавить 0, это значит, что к нему не прибавилось ничего. Слагаемое каким было, таким и осталось, сколько раз ноль ни прибавляй. То же самое будет, если отнять ноль.
Операция умножения гораздо менее очевидна. Не все понимают, почему при умножении на ноль получается ноль. Это объясняется особенностями операции умножения. Изначально ее определяли как число, прибавленное к самому себе определенное количество раз, что справедливо для натуральных чисел. Так, 5 х 3 = 15. Этот пример можно заменить следующим выражением: 5 + 5 + 5 = 15. То есть число 5 было взято 3 раза. Согласно этому правилу, умножение на 0 числа 5 дает нулевой результат, и 5 х 0 = 0.
Чтобы было нагляднее, можно привести следующий пример:
Иногда юные скептики выдвигают следующее возражение: допустим, у мальчика в руке 2 яблока. Если он не съел их, то яблоки не пропадут, они так и останутся в него в руке. Почему же тогда результат равен нулю? Действительно, яблоки из руки никуда не денутся. Но в примере учитываются лишь те из них, которые были съедены, проще говоря, оказались в желудке у мальчика. В последнем случае они туда не попали.
Правило умножения на ноль в математике действительно для любых чисел:
В любом случае произведение будет нулевым. С нулем можно производить следующие действия:
Деление на ноль
Математики говорят, что четыре арифметических действия: сложение, вычитание, умножение и деление неравноправны. Базовыми считаются первое и третье из них (сложение и умножение), а деление и вычитание — производными.
Например, разность между 5 и 2 равна 3. Это действие также можно записать в виде следующего выражения: Х + 2 = 5. Решением уравнения будет число 3. Аналогичное правило действует и для умножения. Деление 6 на 3 можно записать так: Х * 2 = 3.
Для действий с нулем можно использовать следующий прием. Выражение записывают так: Х * 0 = 0. Здесь X может быть равен любому числу. Из этого следует, что невозможно найти число, умножение которого на 0 давало бы произведение, отличное от 0.
Если попытаться найти результат от деления ненулевого числа (например, 5) на ноль, то это действие можно записать так: Х * 0 = 5. Так, при умножении любого числа на ноль получается ноль, у этого уравнения в арифметике нет решения.
Раскрытие неопределенностей
Действиями, связанными с делением на 0, занимается один из разделов высшей математики — математический анализ. В нем используется такое понятие, как бесконечность (бесконечно большая величина). Одно из ее определений — это предел, к которому стремится выражение а/Х при Х, стремящемся к нулю. Здесь а — любое ненулевое действительное число. Если в этом выражении уменьшать значение X, то результат будет увеличиваться, пока, в конце концов, не подойдет к бесконечности. С этой величиной можно делать различные математические действия:
В результате получится бесконечность. Следующие выражения дают в результате полную неопределенность:
Задачи с неопределенностями возникают при вычислении пределов функций, которые заданы формулами, дающими подобные выражения при подстановке предельных значений аргумента. Математики говорят, что результатом таких уравнений будет бесконечное множество чисел. Обычно для их решения используют различные схемы и алгоритмы. Это называется раскрытием неопределенности.
Над нулем можно проделывать все арифметические операции. Единственное ограничение — он не может быть делителем для любого действительного числа. Результатом деления ненулевого числа на ноль в высшей математике считается бесконечность, а деление нуля на ноль дает неопределенность. В арифметике подобные действия считаются невозможными и бессмысленными.
Отрицательная степень
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Свойства степеней
Степень с натуральным показателем в математике имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
Свойство 4: степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень сначала делимое, потом делитель, и первый результат разделить на второй.
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0; 0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно: