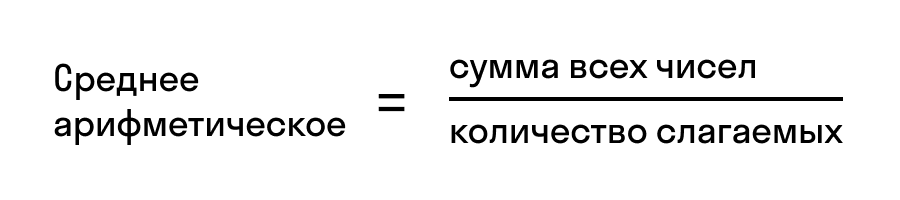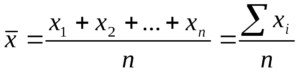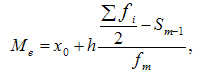Что значит найти среднее арифметическое ряда
Среднее арифметическое
Среднее арифметическое – это частное от деления суммы чисел на их количество.
Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.
Решение: Сначала найдём сумму данных чисел:
Затем разделим полученный результат на количество слагаемых, то есть на 2:
Значит среднее арифметическое двух чисел (4 и 6) равно 5.
Пример 2. Найти среднее арифметическое чисел 15, 8, 20 и 13.
Решение: Сначала найдём сумму данных чисел:
Затем разделим полученный результат на количество слагаемых:
Из данных примеров можно сделать вывод, что для нахождения среднего арифметического, нужно сложить все числа и поделить их сумму на их количество.
Рассмотрим задачи, в которых требуется найти средне арифметическое нескольких чисел, относящихся к одной величине.
Задача 1. Утром температура была 15 градусов, днём она поднялась до 27 градусов, а вечером опустилась до 19, ночью температура достигла отметки в 11 градусов. Найти среднюю температуру за сутки.
Решение: Сначала найдём общую сумму температур за сутки:
15 + 27 + 19 + 11 = 72,
затем разделим полученную сумму на 4:
Ответ: средняя температура за сутки равна 18 градусам.
Задача 2. В магазине продали 6 килограммов яблок по цене 55 рублей за килограмм и 4 килограмма груш по цене 75 рублей за килограмм. Какая средняя цена 1 килограмма фруктов?
Решение: Сначала посчитаем сколько всего денег получил магазин за фрукты:
55 · 6 = 330 (р) — выручка за яблоки;
75 · 4 = 300 (р) — выручка за груши;
330 + 300 = 630 (р) — общая выручка за фрукты.
Затем найдём общий вес фруктов:
теперь разделим общую выручку на общий вес проданных фруктов и получим среднюю цену за 1 кг:
Ответ: средняя цена 1 килограмма проданных фруктов — 63 рубля.
Среднее арифметическое чисел. Мода. Медиана. Размах ряда чисел
Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
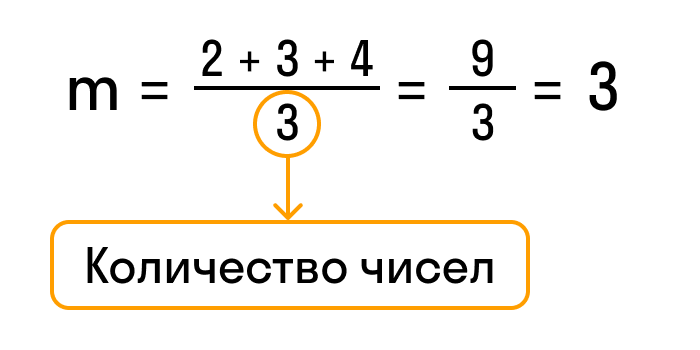
Например: найдем среднее арифметическое чисел 2; 6; 9; 15.
У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Например: найдем размах чисел 2; 5; 8; 12; 33.
Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.
Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.
Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.
Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.
В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.
Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите медиану и размах ряда.
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите моду ряда и среднее арифметическое ряда.
Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.
Найдите среднюю заработную плату.
Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.
Найдите разность среднего арифметического и медианы этого набора.
Найдите объем и медиану числового ряда.
Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:
| I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|
| 37 | 34 | 35 | 32 | 36 | 33 | 38 |
Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.
Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.
Найдите среднее арифметическое этого набора чисел.
Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.
Найдите медиану этого набора чисел.
Провели несколько измерений случайной величины:
800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.
Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.
Найдите разность среднего арифметического и медианы этого набора.
Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.
Найдите среднее арифметическое, размах и моду.
Что значит найти среднее арифметическое ряда
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Для ряда a1,a1. an среднее арифметическое вычисляется по формуле:
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.
Среднее арифметическое: физический смысл и визуализация
Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.
Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.
Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.
Среднее арифметическое двух чисел
Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:
Их среднее арифметическое:
Физический смысл среднего арифметического
Изобразим два исходных числа и их среднее арифметическое на числовой оси:
Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.
В механике момент силы – это произведение силы F на расстояние l:
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l1 и l2, получим:
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:
Обозначив m координату точки опоры весов, получим:
Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:
Координата опоры весов m:
Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.
Визуальное восприятие равновесия
Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.
Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.
Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.
Математическое ожидание случайной величины
Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:
Теперь точка опоры весов в равновесии это μ:
Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:
Это и есть формула математического ожидания.
Гистограмма
Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.
На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.
Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:
Дайте мне точку опоры, и я переверну Землю. Архимед
3 простых формулы, чтобы посчитать среднее арифметическое
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Вот так:
Например, найдем среднее арифметическое чисел 5, 6 и 7. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на три.
Так получилась формула среднего арифметического:
Способы вычисления среднего арифметического
Стандартная формула. Чтобы найти среднее арифметическое, нужно сложить все числа и поделить эту сумму на их количество. Формула выглядит так:
Вычисление моды или наиболее часто встречающегося значения. Формула такая:
Вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. Если такого значения нет, за медиану принимают среднее число между границами половин выборки. Формула выглядит так:
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: в магазине, на работе, в диалоге с другом или во время презентации перед инвесторами. Еще пригодятся, чтобы рассчитать среднюю скорость движения.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Посчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
В 5 классе можно искать среднее арифметическое с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников: