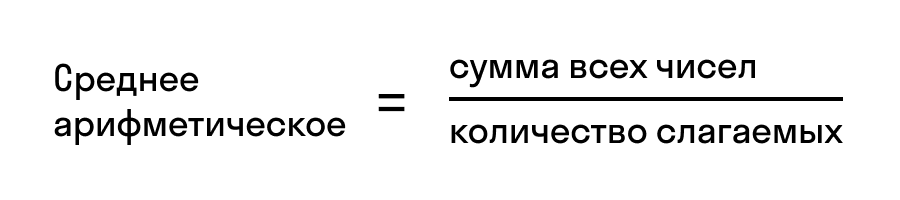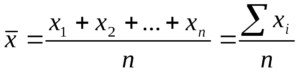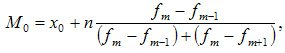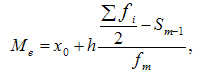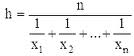Что значит найти среднеарифметическое число

Среднее арифметическое: физический смысл и визуализация

Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:

Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.

Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.

Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.

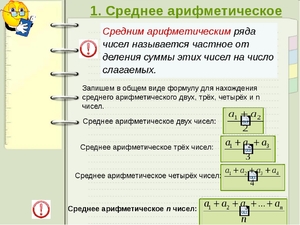
Среднее арифметическое двух чисел

Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:

Их среднее арифметическое:

Физический смысл среднего арифметического

Изобразим два исходных числа и их среднее арифметическое на числовой оси:

Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.

В механике момент силы – это произведение силы F на расстояние l:

На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l₁ и l₂, получим:

Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:

Обозначив m координату точки опоры весов, получим:

Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:

Координата опоры весов m:

Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.

Визуальное восприятие равновесия

Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.

Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:

На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.

Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:

Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.

Математическое ожидание случайной величины

Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:

Теперь точка опоры весов в равновесии это μ:

Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:

Это и есть формула математического ожидания.

Гистограмма

Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.

На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.

Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:

Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:

Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:

Дайте мне точку опоры, и я переверну Землю. Архимед

Источник

Как находить и вычислять для двух среднее арифметическое значение

Под понятием среднего арифметического чисел подразумевается результат несложной последовательности расчётов средней величины для ряда чисел, определённых заранее. Необходимо отметить, что такое значение в данное время широко применяется специалистами ряда отраслей. Например, известны формулы при проведении расчётов экономистами или работниками статистической отрасли, где требуется иметь значение данного типа. Кроме этого, этот показатель активно используют и в ряде других отраслей, которые являются смежными с вышеуказанными.

Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сможет любой желающий. Для этого не надо иметь специальное образование. Часто нет необходимости применять и вычислительную технику.

В качестве ответа на вопрос как найти среднее арифметическое рассмотрим ряд ситуаций.

Подсчёт среднего арифметического пары

Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:

Формула

Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:

В этой формуле применяется следующее обозначение:

А и В – это заранее выбранные числа, для которых необходимо находить значение.

Нахождение значения для трёх

Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:

Формула

Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:

В данной формуле принято следующее обозначение:

А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.

Вычисление среднего арифметического четырёх

Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:

Формула

Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:

В данной формуле переменные имеют следующее значение:

А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.

Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.

Подсчёт среднего арифметического пяти

Выполнение данной операции потребует проведения определённого алгоритма действий.

Формула

Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:

В данной формуле переменные имеют такое обозначение:

А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.

Универсальная формула вычисления

Проводя рассмотрение различных вариантов формул для вычисления среднего арифметического, можно обратить внимание на то, что у них есть общая закономерность.

Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.

Главным при определении формулы является принцип расчёта среднего арифметического.

Данный принцип как было видно из приведённых примеров, выглядит таким образом:

Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:

(А+В+…+N)/N

Данная формула содержит следующие переменные:

А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.

N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.

Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.

Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.

Видео

Из видео вы узнаете, как находить среднее арифметическое.

Источник

Как вычислить среднее арифметическое

Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.

Смысл коэффициента

Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:

Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.

Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.

Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.

Подсчет среднего арифметического

Формула для вычислений предельно проста:

где an – значение величины, n – общее количество значений.

Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.

К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.

Как считать средние для разнородных данных

В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.

Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.

Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.

Рассмотрим пару примеров

Расчет средней оценки

Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:

(3 + 3 + 5 + 4) / 4 = 3,75

Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.

Расчет съеденных конфет

Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.

Заключение

Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.

Источник

3 простых формулы, чтобы посчитать среднее арифметическое

Понятие среднего арифметического

Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Вот так:

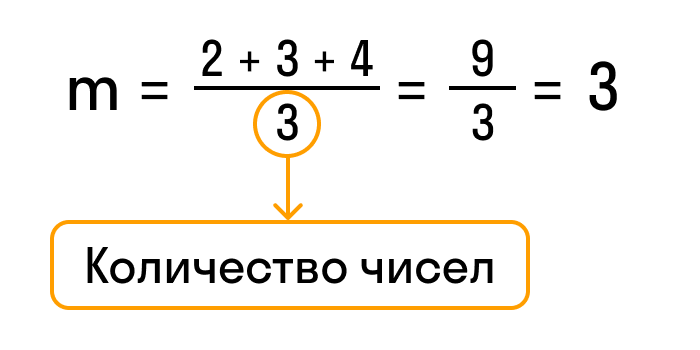
Например, найдем среднее арифметическое чисел 5, 6 и 7. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.

Разделим результат на количество чисел в задании, то есть на три.

Так получилась формула среднего арифметического:

Способы вычисления среднего арифметического

Стандартная формула. Чтобы найти среднее арифметическое, нужно сложить все числа и поделить эту сумму на их количество. Формула выглядит так:

Вычисление моды или наиболее часто встречающегося значения. Формула такая:

Вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. Если такого значения нет, за медиану принимают среднее число между границами половин выборки. Формула выглядит так:

Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: в магазине, на работе, в диалоге с другом или во время презентации перед инвесторами. Еще пригодятся, чтобы рассчитать среднюю скорость движения.

Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:

Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.

Примеры расчета среднего арифметического

Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.

Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.

Пример 2. Посчитать среднее арифметическое 7,5 и 8 и 0,5.

Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.

Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.

Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.

Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.

Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.

Ответ: школьник в неделю тратит в среднем 81 рубль.

В 5 классе можно искать среднее арифметическое с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Источник

Правильное среднее

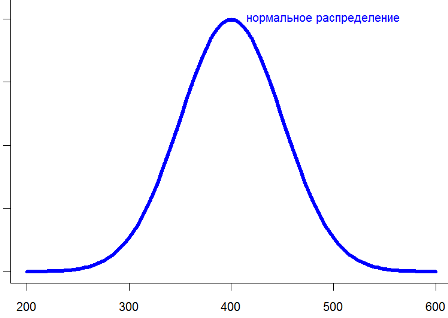
Существует много видов средних, но в каждой ситуации только одно из них правильное. Только один вид среднего следует использовать в каждом конкретном случае, и ошибка может вам стоить очень дорого.

Дело в том, что в основе такого усреднения лежит закон больших чисел и допущение, что исходная величина распределена нормально. А это подразумевает, что возможные значения сконцентрированы вокруг некоторого наиболее частого значения, а отклонения и в большую, и в меньшую сторону относительно невелики и равновероятны.

В следующих записях я приведу интересные примеры неправильного усреднения, а сейчас перейдем к другим видам среднего.

Сначала, наверное, может показаться, что правильное значение 65 км/ч, потому что (50+80)/2 = 65.
Однако быстро становится понятно, что если бы другой автомобиль двигался со средней скоростью, то он провел бы в пути столько же времени, что и первый. Именно в этом смысл усреднения в данном случае.

И вот тут на помощь приходит среднее гармоническое:

Для нашей задачи искомое среднее равно 2/(1/50+1/80)=61.54 км/ч. И действительно в первом случае автомобиль затратил 2 часа на преодоление 100 км со скоростью 50 км/ч и еще 1.25 часа ему потребовалось на следующие 100 км, потому что скорость возросла до 80 км/ч. Таким образом, всего ушло 3.25 часа.
Если бы автомобиль все 200 км двигался со скоростью 61.54 км/ч, то у него также ушло бы на дорогу 3.25 часа.

Можно предположить, что есть несколько вариантов усреднения. Во-первых, среднее арифметическое: (12+42)/2 = 27%. Во-вторых, сложный процент: 1.12*1.42=1.5904, т.е. 59.04% за 2 года или 28.02% за год.

Но «в среднем» означает, что применив это значение к каждому году, мы получим тот же самый результат, что и при использовании множества исходных значений.

Проверяем. Среднее арифметическое: 1.27*1.27=1.6129 (на 61.29%). Сложный процент: 1.2802*1.2802=1.6389 (на 63.89%). Результаты мало того, что разные, так и оба неправильные, потому что выручка за 2 года выросла на 59.04%.

Среднее геометрическое часто встречается в реальных бизнес-задачах вместе с процентами и долями. Если в вашей задаче что-то растет или падает и вы хотите усреднить динамику показателя, то вам следует применять среднее геометрическое.

Вместо заключения
Повторю главные моменты:
— среднее арифметическое далеко не всегда соответствует смыслу и физической сущности усредняемого показателя;
— существует много видов средних значений, но в каждом конкретном случае есть только один правильный вид среднего, и именно его следует использовать в расчетах.

Источник