Что значит найти координаты

Прямоугольная система координат. Ось абсцисс и ординат

Прямоугольная декартова система координат

Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Прямоугольная система координат в трехмерном пространстве

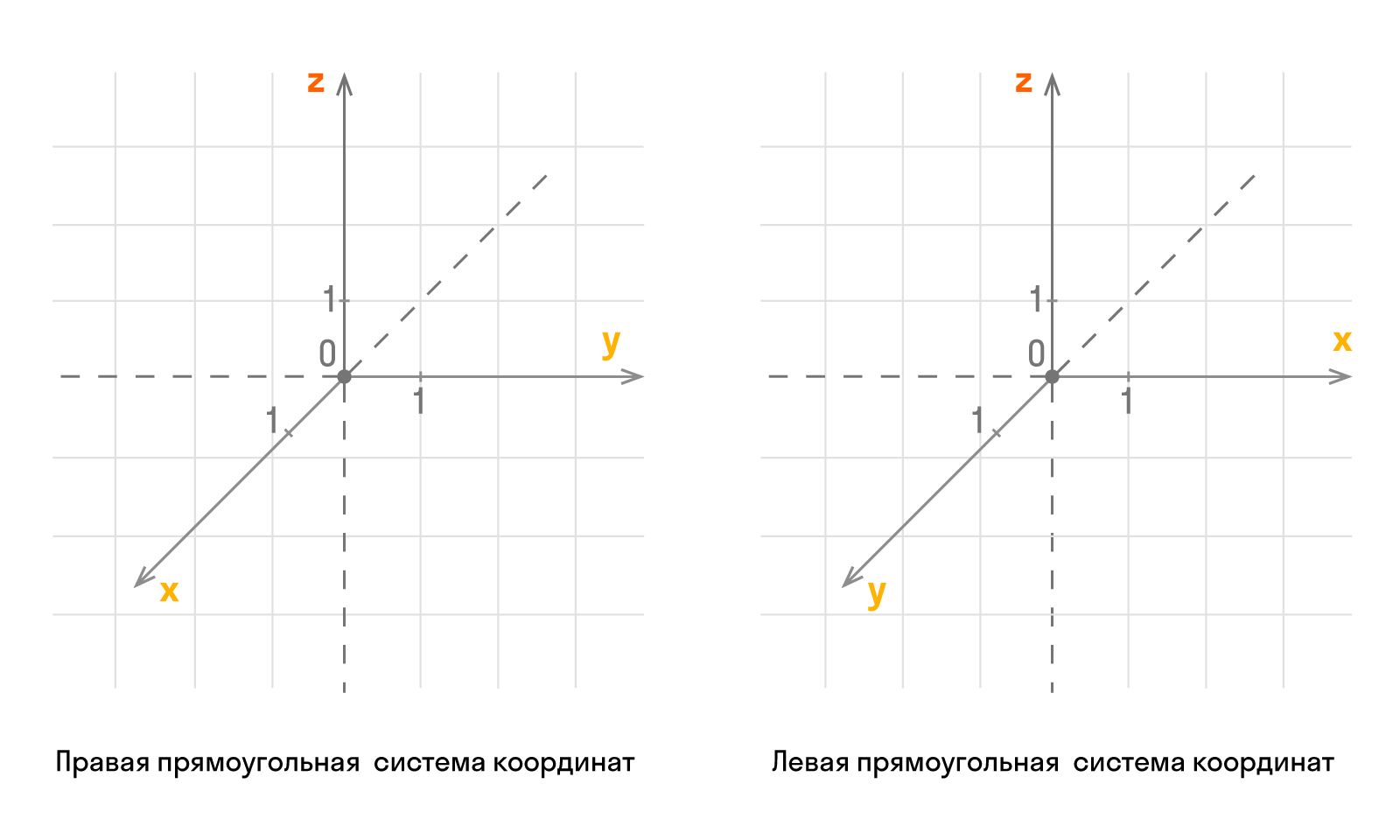
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Координаты точки в трехмерном пространстве

Сформулируем определение точки М в трехмерном пространстве.

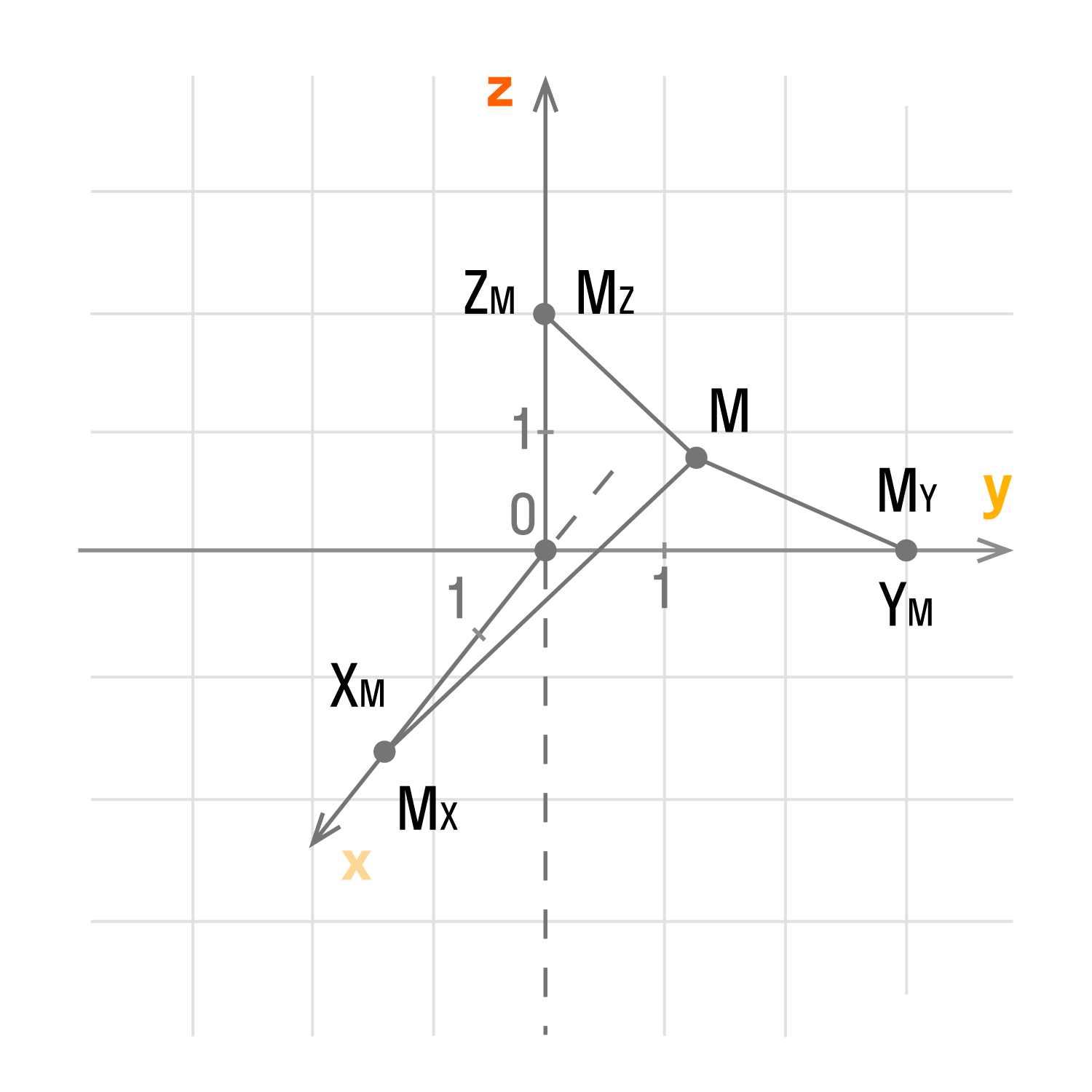
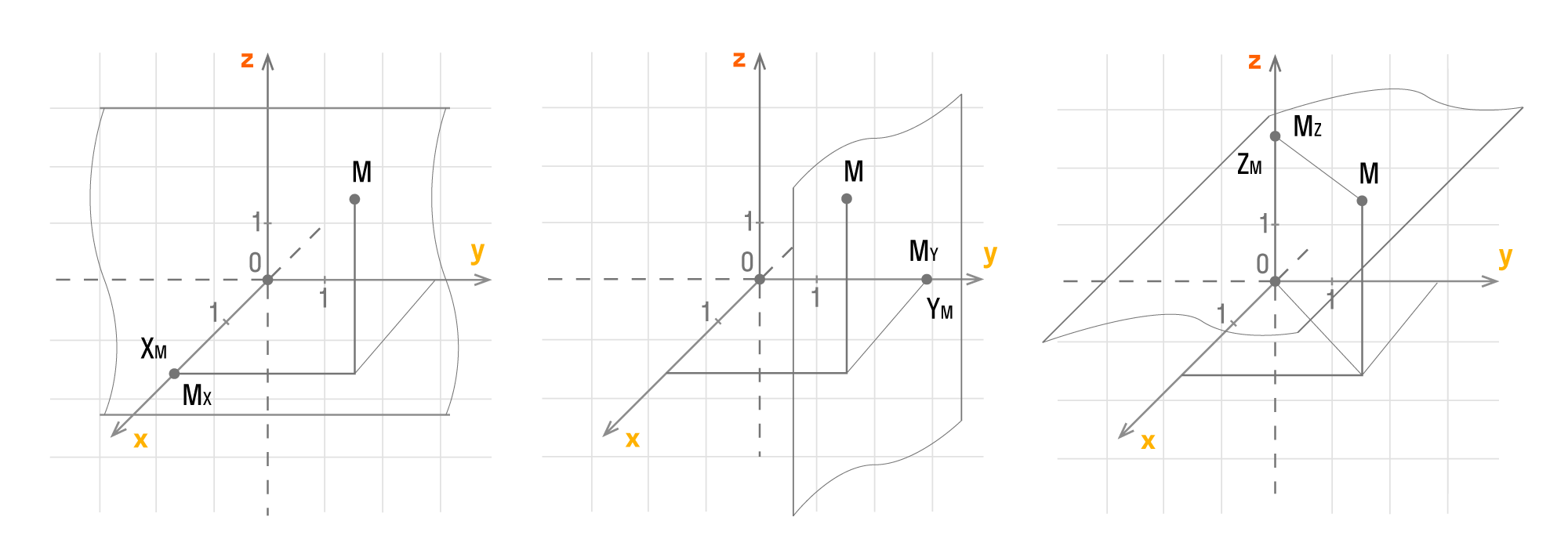
Пусть M_x, M_y, M_z — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения x_M, y_M, z_M. Как это выглядит на координатных прямых:

Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в M_x, M_y, M_z.

У каждой точки трехмерного пространства есть свои данные (x_M, y_M, z_M), которые являются координатами точки М.

x_M, y_M, z_M — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (x_M, y_M, z_M) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.

Источник

Каждая точка поверхности планеты имеет определенное положение, которому соответствует собственная координата по широте и долготе. Она находится на пересечении сферических дуг меридиана, отвечающего за долготу, с параллелью, что соответствует широте. Обозначается парой угловых величин, выраженных в градусах, минутах, секундах, что имеет определение системы координат.

Широта и долгота — это географический аспект плоскости или сферы, перенесенный на топографические изображения. Для более точного нахождения какого-либо пункта берется во внимание также его высота над уровнем моря, что позволяет найти его в трехмерном пространстве.

Необходимость найти точку по координатам широты и долготы возникает по долгу службы и по роду занятий у спасателей, геологов, военных, моряков, археологов, летчиков и водителей, но может понадобиться и туристам, путешественникам, искателям, исследователям.

Что такое широта и как ее найти

Широтой называют расстояние от объекта до линии экватора. Измеряется в угловых единицах (таких как градус, град, минута, секунда и т.д.). Широта на карте либо глобусе обозначается горизонтальными параллелями — линиями, описывающими окружность параллельно экватору и сходящимися в виде ряда сужающихся колец к полюсам.

Поэтому различают широту северную — это вся часть земной поверхности севернее экватора, а также южную — это вся часть поверхности планеты южнее экватора. Экватор — нулевая, самая длинная параллель.

Запомните! Чем ближе к экватору располагается заданная местность, тем меньшей будет ее широта.

Что такое долгота и как ее найти

Долгота — это величина, на которую удалено положение заданной местности относительно Гринвича, то есть нулевого меридиана.

Долготе аналогично присуще измерение в угловых единицах, только с 0° до 180° и с приставкой — восточная либо западная.

Запомните! Чем далее от Гринвича удаляется искомый пункт, тем большей будет его долгота, чем ближе — тем меньшей будет его долгота.

Как найти координаты заданной точки по карте

Зачастую приходится узнавать координаты пункта, который расположен на карте в квадрате между двумя ближайшими параллелями и меридианами. Приблизительные данные можно получить на глазок, оценив последовательно шаг в градусах между нанесенными на карту линиями в интересующем районе, а затем сопоставив удаленность от них искомой местности. Для точных вычислений понадобятся карандаш с линейкой, или же циркуль.

Пример! Расстояние между параллелями 40° и 50°, среди которых находится наша местность, составляет 2 см либо 20 мм, а шаг между ними — 10°. Соответственно, 1° равен 2 мм. Наша точка удалена от сороковой параллели на 0,5 см либо 5 мм. Находим градусы до нашей местности 5/2 = 2,5°, которые нужно прибавить к значению ближайшей параллели: 40° + 2,5° = 42,5° — это наша северная широта заданной точки. В южном полушарии вычисления аналогичны, но результат имеет отрицательный знак.

Аналогично находим долготу — если ближайший меридиан находится дальше от Гринвича, а заданный пункт ближе — то разницу вычитаем, если меридиан к Гринвичу ближе, а пункт дальше — то прибавляем.

Если под рукой нашелся только циркуль, то его его кончиками фиксируется каждый из отрезков, а распор переносится на масштаб.

Похожим образом производятся вычисления координат на поверхности глобуса.

Лучшие сервисы для поиска места по координатам

Проще всего узнать своё местоположение можно, зайдя в ПК-версию сервиса, работающего непосредственно с Google Maps. Многие утилиты упрощают процесс ввода широты и долготы в браузере. Рассмотрим лучшие из них.

Map & Directions

На официальном сайте Maps & Directions можно найти точные GPS-координаты любого пункта, или же выбрать нужное место и посмотреть его ширину и долготу. Пользоваться сервисом очень легко, в него включена опция увеличения масштаба на карте и возможность поделиться своим местоположением.

Кроме того, Maps & Directions позволяет бесплатно определить координаты своего положения на карте, нажав всего на одну кнопку. Щелкните на «Найти мои координаты», и сервис тут же поставит маркер и определит широту, долготу до многих тысячных, а также высоту.

На этом же сайте можно измерить расстояние между населенными пунктами или площадь любой заданной территории, нарисовать маршрут или рассчитать время передвижения. Сервис пригодится как путешественникам, так и просто любопытным пользователям.

Mapcoordinates.net

Полезная утилита Mapcoordinates.net позволяет узнать координату точки в любом регионе мира. Сервис также интегрирован с Google Картами, но обладает упрощенным интерфейсом, благодаря которому его сможет использовать даже неподготовленный пользователь.

В адресной строке утилиты, где написано «Искать», введите адрес места, широту и долготу которого Вы хотите получить. Карта с координатами появится вместе с маркером на нужном месте. Над маркером будет отображена широта, долгота, а также высота выбранной точки.

К сожалению, Mapcoordinates.net не подходит для того, чтобы искать пункты, зная их координаты. Однако для обратной процедуры это очень удобная утилита. Сервис поддерживает множество языков, в том числе и русский.

Поиск по координатам на карте через браузер с помощью сервиса Google Maps

Если по каким-либо причинам Вы предпочитаете работать не с упрощенными сервисами, а непосредственно с Google Maps, то эта инструкция будет полезной для Вас. Процесс поиска по координатам через Google Карты чуть более сложен, чем в описанных ранее способах, но им можно овладеть быстро и без особого труда.

Чтобы узнать точные координаты места, придерживайтесь следующей простой инструкции:

Откройте сервис на ПК. Важно, что должен быть включен полный, а не облегченный (отмечается специальным значком молнии) режим, иначе получить информацию не получится;

Щелкните на участок карты, где расположен нужный Вам пункт или точка, правой кнопкой мыши;

Отметьте в появившемся меню вариант «Что здесь?»;

Посмотрите на вкладку, которая отобразится внизу экрана. На ней будут отображены широта, долгота и высота.

Чтобы определить место по известным географическим координатам, потребуется другой порядок действий:

Откройте Google Карты в полном режиме на компьютере;

В строке поиска в верхней части экрана Вы можете ввести координаты. Сделать это допускается в следующих форматах: градусы, минуты и секунды; градусы и десятичные минуты; десятичные градусы;

Нажмите клавишу «Enter», и на карте на требуемом месте появится специальный маркер.

Важнее всего при использовании сервиса Google Maps правильно указывать географические координаты. Карты распознают только несколько форматов данных, поэтому обязательно учитывайте следующие правила ввода:

При вводе градусов используйте специальный символ, обозначающий его «°», а не «d»;

В качестве разделителя между целой и дробной частями необходимо использовать точку, а не запятую, иначе строка поиска не сможет выдать место;

Найти специальный символ на клавиатуре ПК затруднительно, да и чтобы придерживаться необходимого списка правил, нужно прикладывать достаточно много усилий. Гораздо проще пользоваться специальными утилитами — лучшие из них мы привели в разделе выше.

Нахождение места по широте и долготе на ОС Андроид

Нередко требуется найти место по координатам вдали от ноутбука или персонального компьютера. Выручит мобильное приложение Google Maps, работающее на платформе Андроид. Обычно оно используется для того, чтобы проложить маршрут или узнать график движения транспортных средств, однако программа подойдет и для нахождения местоположения пункта или точки.

Скачать приложение на на Андроид можно на официальной странице в Google Play. Оно доступно как на русском, так и на английском языках. После установки программы придерживайтесь следующей инструкции:

Откройте Google Maps на устройстве и дождитесь появления карты;

Найдите интересующее Вас место. Нажмите на него и держите до тех пор, пока не отобразится специальный маркер;

Вверху экрана появится вкладка с окном поиска и полными координатами места;

Если Вам нужно найти место по координатам, а не наоборот, то способ на мобильном устройстве ничем не отличается от своего аналога на ПК.

Мобильная версия сервиса, как и работающая на ПК, позволит детально изучить нужное место, узнать его точные координаты, или наоборот, распознать адрес по известным данным. Это — удобный способ как для дома, так и для дороги.

Источник

Шкалы, координаты

Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.

Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.

Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).

Рисунок 1. Измерительная линейка.

Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.

Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).

Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.

Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.

Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.

Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.

Рисунок 2 Цена деления шкалы

Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?

Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:

Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.

Координатный луч, единичный отрезок, координаты точки

Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.

Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.

Рис. 3. Луч с началом в точке O

Рис. 4. Луч с равными отрезками

Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).

Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.

Рис. 5. Луч с отрезками и цифрами

Покажу еще раз на примере точки S :

так как RS=OP (по условиям построения данных отрезков),

подставив известные нам значения длины отрезков OR и OP, получим:

Значит, точке S на нашем лучу соответствует число 3.

Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.

Рис. 6. Координатный луч

Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.

Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.

Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.

Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.

Координатный луч — это не что иное, как бесконечная шкала.

Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.

Рис. 7. Разные варианты единичного отрезка

Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).

Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.

Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.

Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.

Рис. 8. Координаты точек

Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).

В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.

Рис. 9. Большие числа на координатном луче.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.1 / 5. Количество оценок: 8

Источник