Что значит найти координаты проекции точек

Проекция точки на прямую, координаты проекции точки на прямую.

В этой статье сначала дано определение проекции точки на прямую (на ось) и приведен поясняющий рисунок. Далее разобран способ нахождения координат проекции точки на прямую во введенной прямоугольной системе координат на плоскости и в трехмерном пространстве, показаны решения примеров с подробными пояснениями.

Навигация по странице.

Проекция точки на прямую – определение.

Вообще проецирование некоторой фигуры на прямую является обобщением понятия ортогонального проецирования фигуры на плоскость (смотрите статью проекция точки на плоскость).

Так как все геометрические фигуры состоят из точек, а проекция фигуры представляет собой множество проекций всех точек этой фигуры, то для проецирования фигуры на прямую необходимо уметь проецировать точки этой фигуры на данную прямую.

Так что же называют проекцией точки на прямую?

Проекция точки на прямую – это либо сама точка, если она лежит на данной прямой, либо основание перпендикуляра, опущенного из этой точки на заданную прямую.

Это определение проекции точки на прямую справедливо как для случая на плоскости, так и для случая в трехмерном пространстве.

Нахождение координат проекции точки на прямую – теория и примеры.

Начнем с нахождения координат проекции точки на прямую, когда проецируемая точка и прямая заданы в прямоугольной системе координат Oxy на плоскости. После этого покажем, как находятся координаты проекции точки на прямую в прямоугольной системе координат Oxyz в трехмерном пространстве.

Координаты проекции точки на прямую на плоскости.

Из проведенного построения логически следует алгоритм, позволяющий найти координаты проекции точки на прямую a :

Разберемся с нахождением координат проекции точки на прямую при решении примера.

Уравнение прямой a нам известно из условия, так что можно переходить ко второму шагу алгоритма.

Таким образом, проекция точки на прямую имеет координаты .

.

Для нахождения координат проекции точки М₁ на прямую АВ будем действовать по полученному алгоритму.

Напишем уравнение прямой, проходящей через две заданные точки и :
.

Чтобы определить координаты проекции точки на прямую АВ осталось решить систему уравнений :

.

Какие координаты имеют проекции точки на координатную прямую Oy и на прямую .

Проекцией точки на прямую Oy является точка с координатами .

Перепишем уравнение прямой как . Теперь хорошо видно, что проекция точки на прямую имеет координаты .

и .

Координаты проекции точки на прямую в трехмерном пространстве.

Рассмотрим решение примера.

Для определения координат проекции точки М₁ на прямую a воспользуемся полученным алгоритмом.

Уравнения прямой a нам сразу известны из условия, так что переходим ко второму шагу.

Из канонических уравнений прямой a получим уравнения двух пересекающихся плоскостей, которые определяют прямую a:

Координаты точки пересечения прямой и плоскости мы получим, решив систему линейных уравнений вида . Применим метод Крамера (если Вам больше нравиться метод Гаусса или какой-нибудь другой метод решения систем линейных уравнений, то применяйте его):

Теперь мы можем вычислить искомые координаты точки пересечения прямой a и плоскости по параметрическим уравнениям прямой a при :
.

То есть, проекция точки М₁ на прямую a имеет координаты .

.

Источник

Как найти проекцию точки на плоскость: методика определения и пример решения задачи

При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.

Уравнение для описания плоскости

Вам будет интересно: МС: что это такое?

Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:

Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.

Понятие о проекции точки и ее вычисление

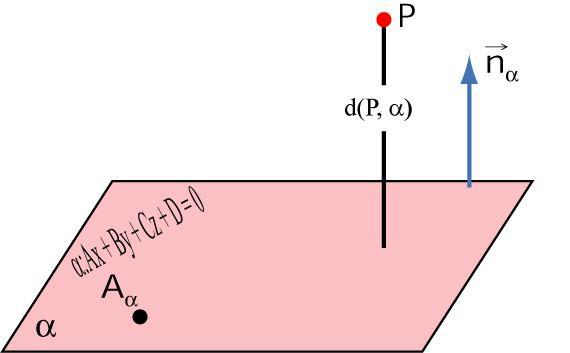
Предположим, что задана некоторая точка P(x1; y1; z1) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x2; y2; z2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.

Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:

(x; y; z) = (x1; y1; z1) + λ*(A; B; C).

После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.

Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.

Вычисление расстояния от плоскости до точки

Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:

Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.

Пример задачи

Следует найти точки проекцию на плоскость и вычислить между ними расстояние.

В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90o. Имеем:

Записывая это равенство в явном виде, приходим к следующей системе уравнений:

Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:

Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:

Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:

В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.

Источник

Точка. Проекция точки на ось.

Ось это прямая линия, на которой выделено одно из двух возможных ее направлений (направление выбирается исходя из условий задания).

Любую ось можно задать произвольным вектором, который должен лежать на оси и иметь одинаковое с этой осью направление.

Например, ось можно задать вектором или (однако нельзя задать с помощью вектора ).

Зададимся осью ОХ и некоторой точкой М (вне оси или лежащая на ней). При проведении через точку М плоскости, перпендикулярной оси; она пересечет ось в точке М’.

Проекция точки М на ось ОХ в данном случае есть точка М’, однако если точка М лежит на оси, то она сама является своей проекцией.

Иначе сказать, проекция точки М на ось ОХ это основание перпендикуляра, который проведен из точки М на ось ОХ.

Рассмотренное выше определение четко показывает, что построение выполняется в пространстве.

Источник

Черчение. 10 класс

§ 16. Проекции точек на поверхностях геометрических тел

Проекции точек на поверхностях геометрических тел

Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.

Укажите количество вершин, ребер и граней изображенного предмета.

Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки.

Рассмотрим проекции точки на геометрических телах.

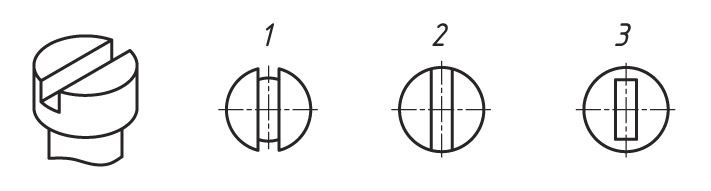
Проецирование точек на поверхности цилиндра

Последовательность проецирования точек
Заданы фронтальные проекции а″ и b″ точек А и В, лежащие на боковой поверхности цилиндра. Проекция а″ находится на видимой части поверхности цилиндра (на плоскости V показана без скобок), b″ находится на невидимой части поверхности цилиндра (на плоскости V показана в скобках).

1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью.

2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи.

Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).

Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.

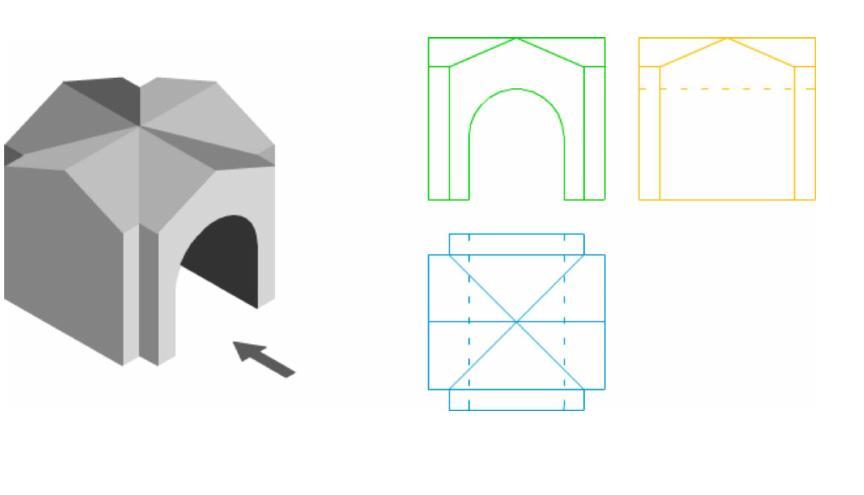
Проецирование точек на поверхности призмы

Последовательность проецирования точек
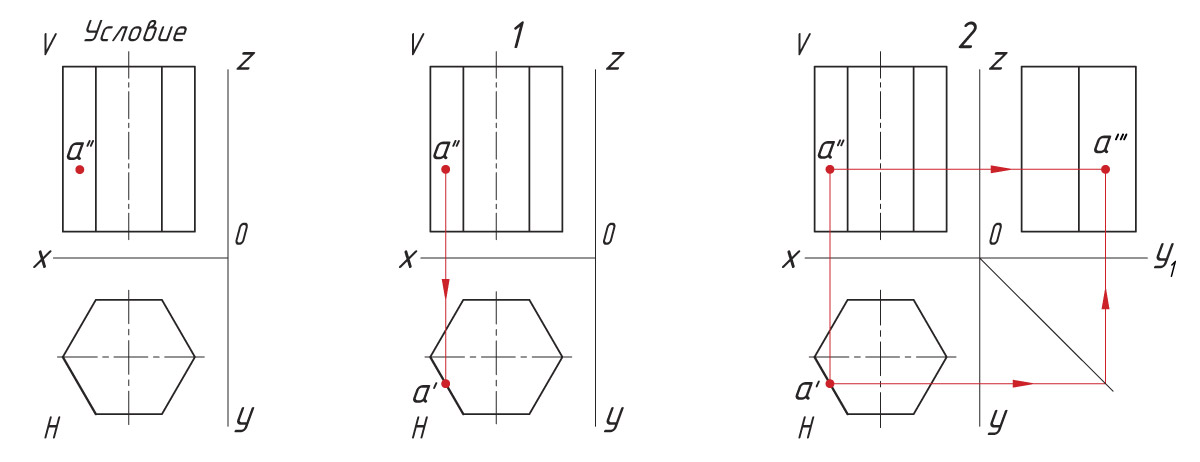
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности шестигранной призмы.

1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы).

2. Проекцию точки а′″ находят на пересечении линий проекционной связи.

Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.

Проецирование точек на поверхности пирамиды

Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.

Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.

Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.

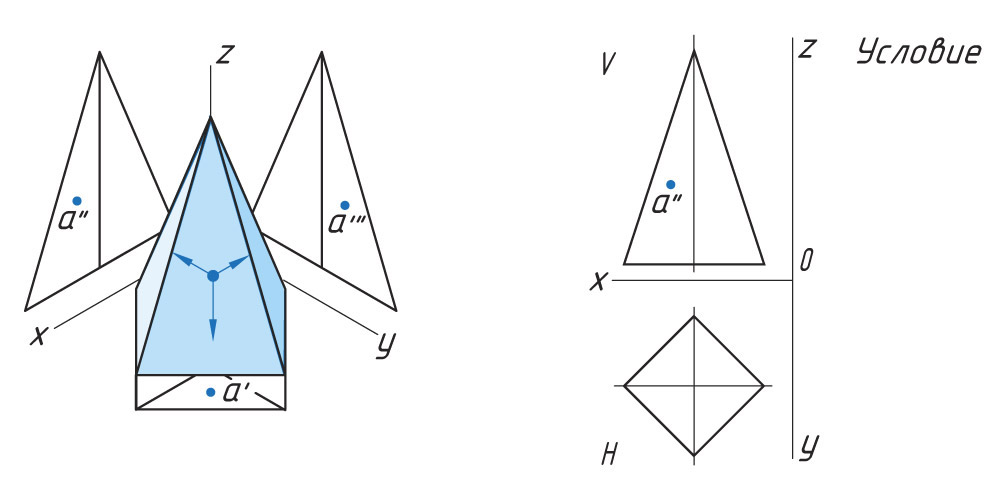
Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.

Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.

Способ I.

1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″.
2. Проводят вертикальную линию связи из проекции f″ до пересечения с основанием на плоскости H в точке f′.
3. Точку f′ соединяют с вершиной пирамиды s′. На нее проводят вертикальную линию связи из проекции а″ до пересечения в точке а′.
4. Проекции точки а′″ находят на пересечении линий проекционной связи.

Способ II.

1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″.
2. Опустив из точки 1″ вертикальную линию связи до пересечения с соответствующим ребром на плоскости H, получают горизонтальную проекцию точки 1′.
3. Для нахождения проекции 2′ проводят из точки 1′ вспомогательную прямую, параллельную основанию до пересечения с ребром.
4. Горизонтальную проекцию а′ определяют, опустив вертикальную линию связи из точки а″ до пересечения со вспомогательной прямой 1′2′.
5. Проекцию точки а′″ находят на пересечении линий проекционной связи.

На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?

Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами.

Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А.
В способе II через точку А проводят вспомогательную плоскость, которая пересечет конус по окружности, расположенной в плоскости, параллельной основанию конуса.

Источник

Проекция точки на плоскость онлайн

С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Проекция точки на плоскость − теория, примеры и решения

Для нахождения проекции точки M₀ на плоскость α, необходимо:

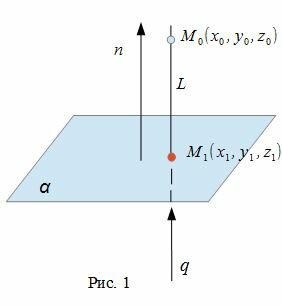Общее уравнение плоскости имеет вид:

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональной плоскости (1) имеет следующий вид:

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

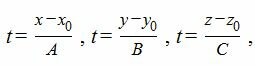Выразим переменные x, y, z через рараметр t.

Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

Подставляя значение параметра t в выражения (4), находим проекцию M₁ точки M₀ на плоскость (1).

Нормальный вектор плоскости имеет вид:

Подставляя координаты точки M₀ и нормального вектора плоскости в (5), получим:

Из выражений (7) находим:

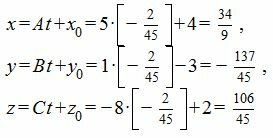Источник