Что значит найти функцию

Что такое Функция?

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Определение функции. Способы задания функции.

Что значить задать функцию? Какими способами можно задать функцию? Что такое определение функции?

Задать функцию — это значит указать правило, при задании любого значения аргумента x вы найдете значение функции y.

Функция y=f(x) – зависимость переменной y от переменной x. Когда задаем значение аргумента x, получаем единственное значение функции y.

Способы задания функции.

В данной статье рассмотрим 3 способа задания функции. На самом деле их больше, в школьной программе чаще всего разбирают эти способы задания функции.

Аналитический способ задания функции.

Чаще всего в школьной программе правило задают в виде формулы y=f(x), x∈X или нескольких формул. Такой способ задания функции называется аналитическим.

Примеры аналитического задания функции:

Графический способ задания функции.

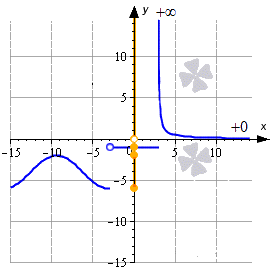
Также если по формуле построить график функции, то данный способ задания функции будет называться графическим. Не всегда вам будут давать график совместно с формулой. Иногда вам в заданиях будут давать только график функции, по которому вы должны будете найти определенные данные. По графику функции можно восстановить его формулу, но это не всегда легко сделать, все зависит от начерченного графика. В школьной программе вам будут задавать графики, по которым вы сможете рассчитать формулу.

Примеры, графического задания функции:

Табличный способ задания функции.

Следующий способ задания функции применяется чаще всего на практике называется табличный.

Все данные представлены в виде таблице. У этого способа имеется конечное множество значений аргумента. Такими таблицами вы уже пользовались в алгебре, например, таблица квадратов, таблица корней и т.д.

Примеры, табличного задания функции:

Рассмотрим примеры по теме «Способы задания функции»:

Пример №1:

Является ли графическим заданием какой-либо функции фигура?

Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Пример №2:

Является ли графическим заданием какой-либо функции фигура?

Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Пример №3:

Является ли графическим заданием какой-либо функции фигура?

При проведении вертикальных линий у нас имеется два пересечения. То есть у одной вертикальной линии два пересечения с фигурой. По определению переменной x должно соответствовать только одно значение переменной y, а у нас два пересечения фигуры. Следовательно, данная фигура не является графиком функции.

Источник

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.

теория по математике 📈 функции

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!

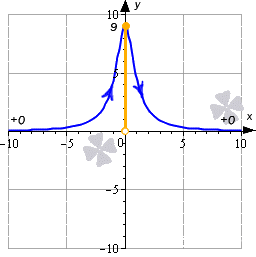
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Таким образом, мы нашли нуль функции: х=2

Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

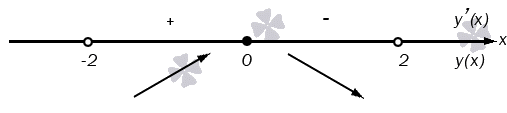
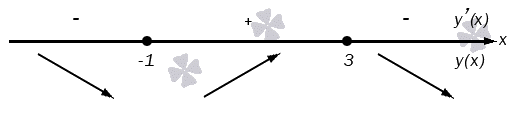
Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Источник

Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения

Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.

В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.

Начнем с базовых определений.

Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.

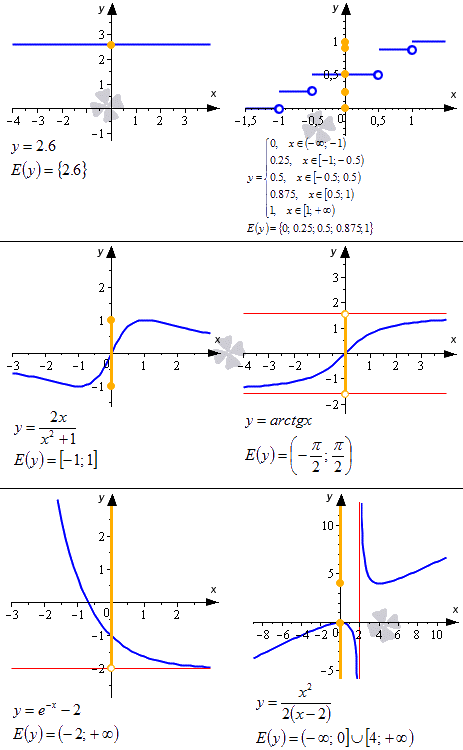
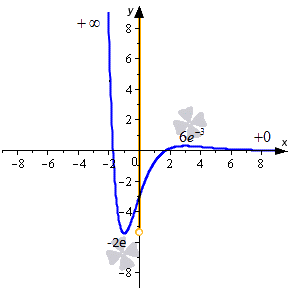
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.

Рассмотрим основные способы нахождения области значений функции.

Возьмем задачу, в которой нужно определить область значений арксинуса.

Решение

Решение

Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.

Для определения точек экстремума надо произвести следующие вычисления:

Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.

Решение

Определяем наибольшее и наименьшее значение функции на заданном отрезке

Решение

Решение

Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.

Ответ: множество всех действительных чисел – область значений функции натурального логарифма.

Решение

Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:

Посмотрим, как же ведет себя функция на бесконечности:

Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.

На нем видно, что областью значений функции будет интервал E ( y ) = ( 0 ; 9 ]

Ответ: E ( y ) = ( 0 ; 9 ]

А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.

Решение

Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:

Это можно увидеть на графике:

Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.

Решение

Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.

Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.

Решение

Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.

Решение

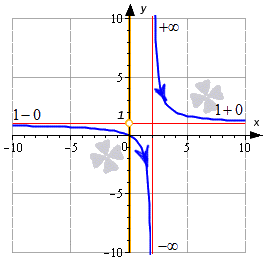
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.

Решение

Решение показано на графике:

Решение

Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:

Теперь найдем соответствующие значения функции:

Посмотрим на поведение функции на бесконечности:

Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.

Источник

Область определения функции

Понятие области определения функции

Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.

Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.

Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).

Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.

Из понятия функции сформулируем определение области определения функции.

Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.

Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.

Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].

Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:

Например, все действительные числа от 2 до 5 включительно можно записать так:

Все положительные числа можно описать так:

Ноль не положительное число, поэтому скобка возле него круглая.

Области определения основных элементарных функций

Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.

На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.

Рассмотрим области определения основных элементарных функций.

Область определения постоянной функции

Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.

Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.

Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.

Область определения функции с корнем

Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.

Рассмотрим две вариации такой функции.

Область определения корня зависит от четности или нечетности показателя:

Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).

Пример

Найти область определения функции:

Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.

Разложим квадратный трёхчлен на множители:

Дискриминант положительный. Ищем корни:

Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).

Область определения степенной функции

Область определения степенной функции зависит от значения показателя степени.

Перечислим возможные случаи:

Рассмотрим несколько примеров.

Область определения показательной функции

Область определения показательной функции — это множество R.

Примеры показательных функций:

Область определения каждой из них (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выглядит так: y = log_ax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.

Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:

Рассмотрим примеры логарифмических функций:

Область определения этих функций есть множество (0, +∞).

Пример

Укажите, какова область определения функции:

Составим и решим систему:

Область определения тригонометрических функций

Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.

Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.

Пример

Найдите область определения функции f(x) = tg2x.

Так как a(x) = 2x, то в область определения не войдут следующие точки:

Перенесем 2 из левой части в знаменатель правой части:

В результате . Отразим графически:

Ответ: область определения: .

Область определения обратных тригонометрических функций

Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.

Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.

Таблица областей определения функций

Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.

И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.

Функция

Область определения функции

Источник