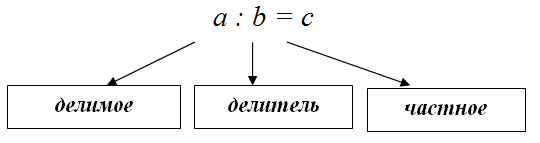
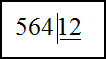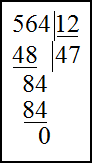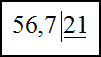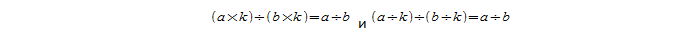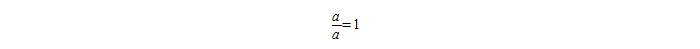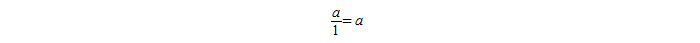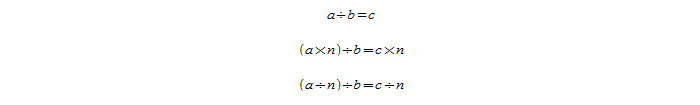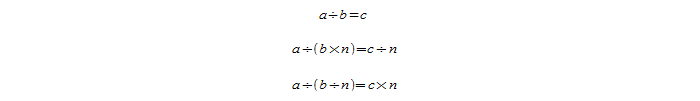Что значит найти частное
Что такое частное чисел
Определение частного чисел
Задание. Найти частное чисел:
Для нахождения частного больших чисел или десятичных дробей используют способ деления в столбик.
Что такое частное чисел не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти частное чисел:
Решение. Для нахождения частного в первом примере выполним деление в столбик. Для этого запишем делимое и делитель следующим образом
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число. Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее запишем полученные числа в столбик, как и в первом примере:
Частное рациональных дробей находится по правилу
Задание. Найти частное рациональных дробей:
Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:
Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей. Для этого целую часть умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Частное в математике — определение, свойства и формула
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Что такое частное в математике?
Математика – уникальная наука, которая привлекает точностью и последовательностью. Каждый, кто начал изучать эту важную дисциплину, должен разобраться, что такое частное в математике.
Деление
В математике есть четыре простейших операции:
Если мы говорим о частном, то нас будет интересовать такая операция, как деление.
Деление всегда обратно умножению. Это математическая величина, которую мы получим, разделив одно число на другое. Есть ряд символов, которые обозначают его:
В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.
Частное рассказывает, во сколько раз одно число больше другого.
Наглядные примеры
Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.
Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:
Запишем простой пример из математики:
80:2=40
80 – делимое (оно делится)
2 – это делитель (на него разделяют)
Восемьдесят больше, чем сорок, в два раза.
Другой пример выглядит так:
120:2=60
Сто двадцать больше, чем шестьдесят, в два раза.
Проверка
Если вы провели операцию деления и сомневаетесь в результате, на помощь придет проверка. Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:
Если после знака равно вы увидели знакомое вам делимое, то можете поставить себе твердую пятерку. Вы научились находить частное чисел и делать проверку. Это очень важно, чтобы в дальнейшем освоить более сложные понятия в алгебре и геометрии.
Частное – это основа математики. Если ученик не смог понять его суть, то двигаться дальше просто бессмысленно. Обратитесь к учителю, если это понятие так и осталось для вас туманным. Педагог разъяснит все ошибки и укажет на подводные камни.
Полное и неполное частное
В результате проведения математических подсчетов частное может быть двух видов:
100:2=50
50 – полное частное
51:2=25 (остаток 1)
25 – неполное частное
1 – остаток от деления
Если вы откроете учебник математики, то увидите, что частное в задачах обозначают при помощи различных символов (переменных). Для этого используют латинские буквы:
30:6=x
Чтобы найти частное, следует делимое разделить на делитель:
Ответ 5 – это частное в данном примере.
Абстрактные определения и туманные рассуждения плохо усваиваются мозгом школьника. Поэтому всегда держите под рукой задачник со списком упражнений по математике. Он поможет понять различные математические категории на практике. Конкретные цифры, записанные в тетради, станут главными помощниками.
Быстрое нахождение однозначного частного
Занимаясь с учениками младших и средних классов, я часто вижу у них затруднения в быстром нахождении нужной цифры частного при выполнении промежуточных вычислений действия деления или непосредственно деления многозначных чисел. А между тем, этот навык достаточно простой, и освоив его, любые вычисления, связанные с делением, станут более легкими и быстрыми.
Как узнать, будет ли частное однозначным
Прежде всего, нужно научиться узнавать, получится в результате деления однозначное или многозначное число?
Чтобы это определить, нужно в уме быстро умножить делитель на 10 (самое маленькое многозначное число).
Если полученное произведение больше делимого, тогда частное получится меньше десяти, а значит, оно – однозначное число, а если делимое окажется больше, то частное будет точно больше десяти, а значит, оно – многозначное.
Рассмотрим пример \( \textcolor
Теперь другой пример \( \textcolor
Как найти однозначное частное
Рассмотрим два случая, когда в результате деления двух чисел получается однозначное число:
В случае, если делитель и частное – однозначные числа, на помощь приходит таблица умножения.
Во втором случае, если делитель – многозначное число, а частное – однозначное, то это частное находится при помощи испытаний одной или нескольких цифр.
Я научу вас более простому способу.
1. В делителе берем цифру самого большого разряда (первую слева), а остальные цифры мысленно отбрасываем.
То есть, в нашем случае оставляем только 5 тысяч, а три цифры младших разрядов отбрасываем.
2. В делимом также мысленно отбрасываем столько же цифр младших разрядов, сколько отбросили в делителе.
В нашем примере мысленно отбрасываем от делимого 36924 три цифры справа, и получаем 36 тысяч.
Как видите, в этом приеме нет ничего особо сложного. Попрактиковавшись определенное количество времени, вы без труда сможете быстро и достаточно легко проводить необходимые вычисления.