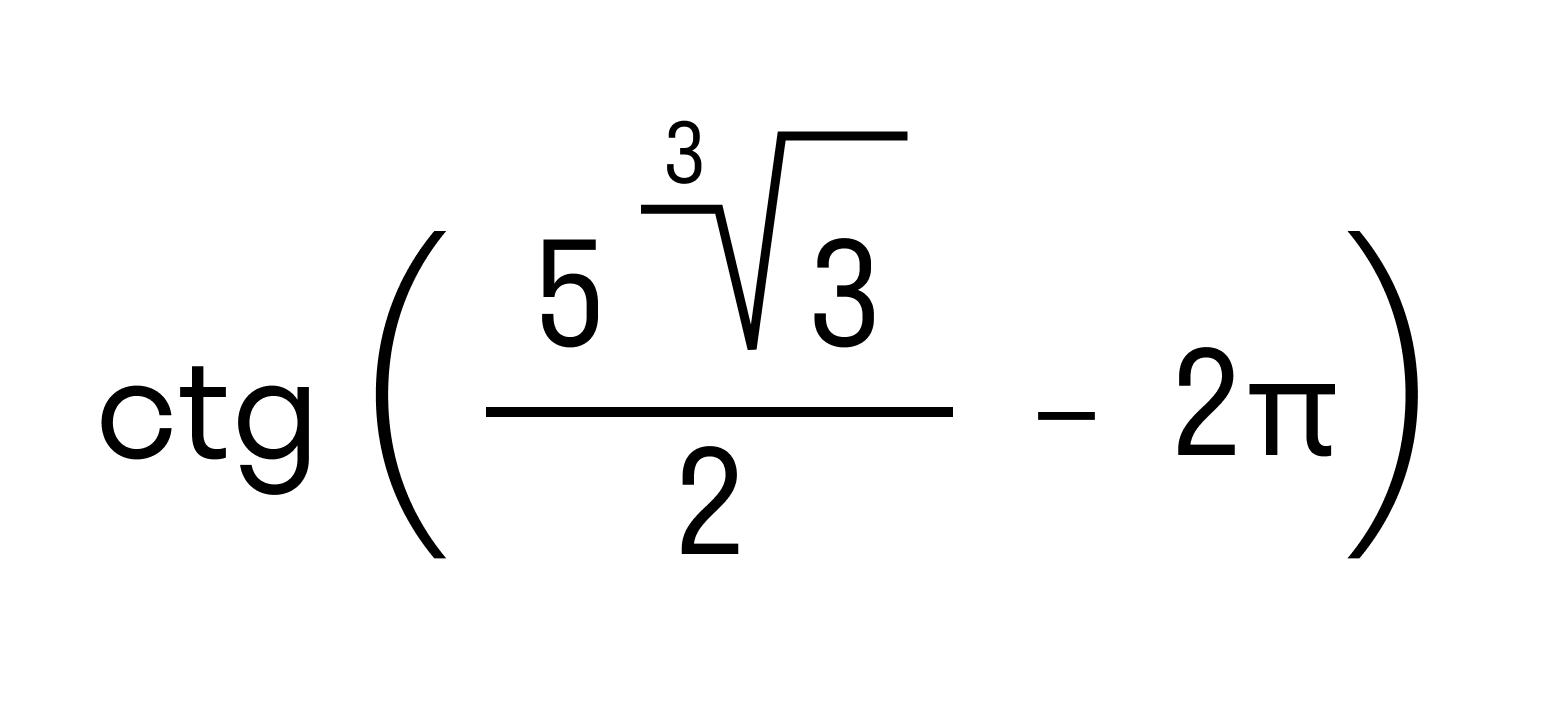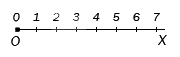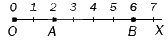Что значит наименьшее числовое значение
Какие числа называются целыми
Определение целых чисел
Что важно знать о целых числах:
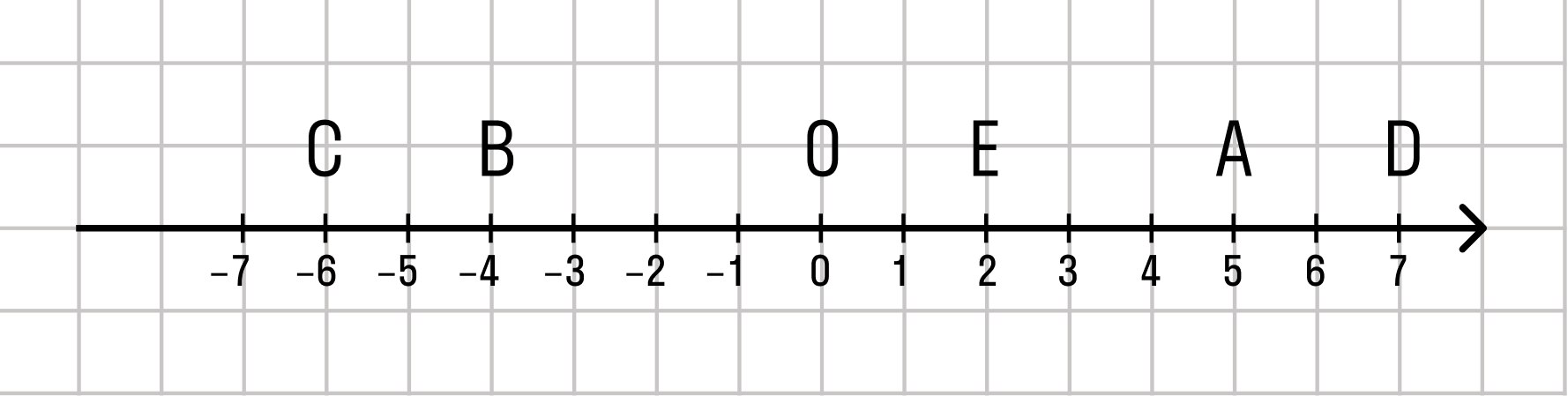
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
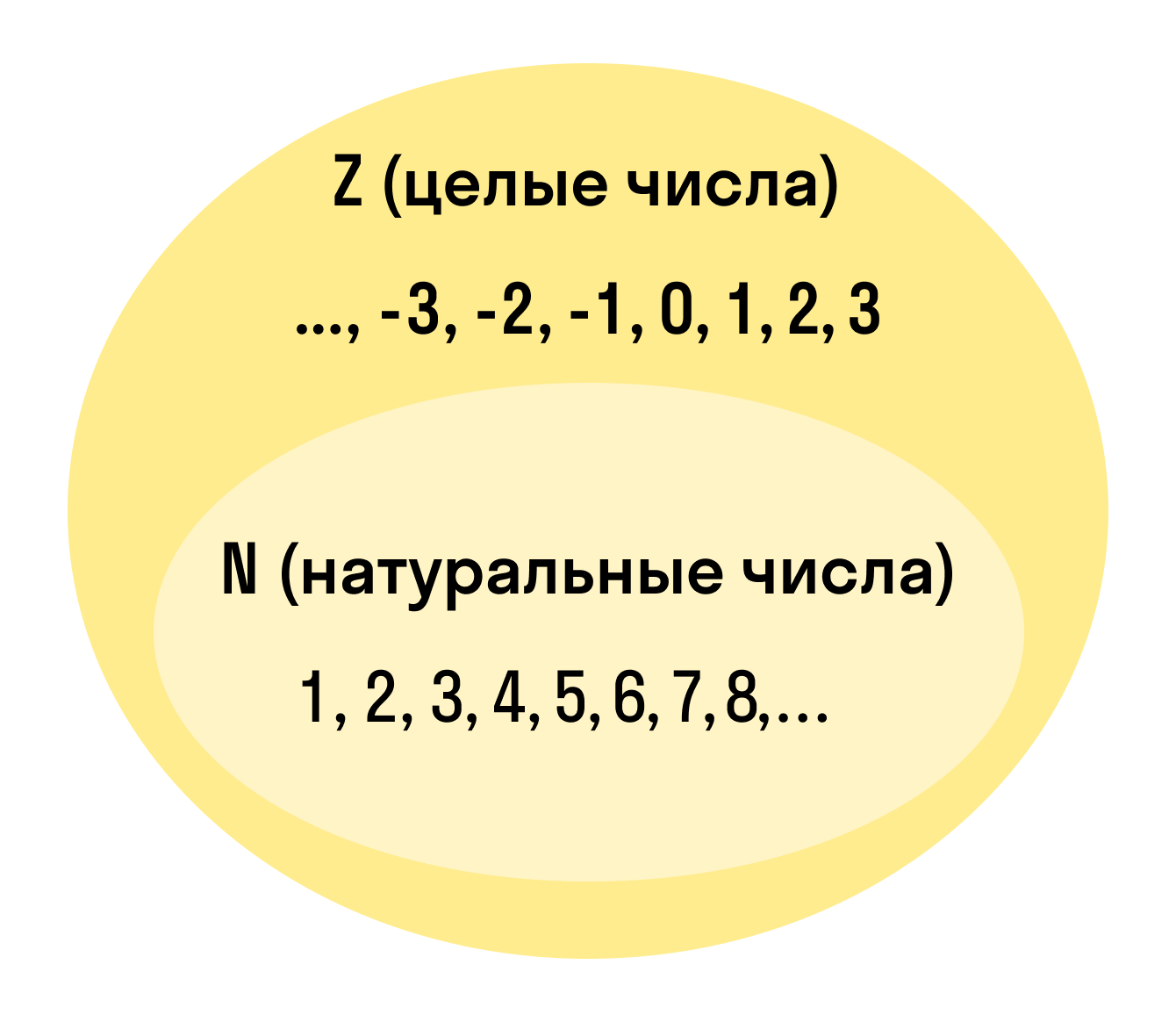
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Изучение точного предмета: натуральные числа это какие числа, примеры и свойства
В математике существует несколько различных множеств чисел: действительные, комплексные, целые, рациональные, иррациональные, дробные… В нашей повседневной жизни мы чаще всего используем натуральные числа, так как мы сталкиваемся с ними при счете и при поиске, обозначении количества предметов….
Какие числа называются натуральными
Из десяти цифр можно записать абсолютно любую существующую сумму классов и разрядов. Натуральными значениями считаются те, которые используются:
N значения всегда целые и положительные. Наибольшего N не существует, так как множество целых значений не ограничено.
Внимание! Натуральные числа получаются при счете предметов или при обозначении их количества.
Абсолютно любое число может быть разложено и представлено в виде разрядных слагаемых, например: 8.346.809=8 миллионов+346 тысяч+809 единиц.
Множество N
Множество N находится в множестве действительных, целых и положительных. На схеме множеств они бы находились друг в друге, так как множество натуральных является их частью.
Множество натуральных чисел обозначается буквой N. Это множество имеет начало, но не имеет конца.
Еще существует расширенное множество N, где включается нуль.
Наименьшее натуральное число
Но в иностранных математических школах, например во французской, нуль считается натуральным. Наличие в ряде нуля облегчает доказательство некоторых теорем.
Ряд значений N, включающий в себя нуль, называется расширенным и обозначается символом N0 (нулевой индекс).
Ряд натуральных чисел
N ряд – это последовательность всех N совокупностей цифр. Эта последовательность не имеет конца.
Особенность натурального ряда заключается в том, что последующее число будет отличаться на единицу от предыдущего, то есть возрастать. Но значения не могут быть отрицательными.
Внимание! Для удобства счета существуют классы и разряды:
Все N
Все N находятся во множестве действительных, целых, неотрицательных значений. Они являются их составной частью.
Эти значения уходят в бесконечность, они могут принадлежать классам миллионов, миллиардов, квинтиллионов и т.д.
Например:
Последовательность в N

от нуля до плюс бесконечности, включая концы, и от единицы до плюс бесконечности, включая концы, то есть все положительные целые ответы.
N совокупности цифр могут быть как четными, так и не четными. Рассмотрим понятие нечетности.
Нечетные (любые нечетные оканчиваются на цифры 1, 3, 5, 7, 9.) при делении на два имеют остаток. Например, 7:2=3,5, 11:2=5,5, 23:2=11,5.
Что значит четные N
Любые четные суммы классов оканчиваются на цифры: 0, 2, 4, 6, 8. При делении четных N на 2, остатка не будет, то есть в результате получается целый ответ. Например, 50:2=25, 100:2=50, 3456:2=1728.
Важно! Числовой ряд из N не может состоять только из четных или нечетных значений, так как они должны чередоваться: за четным всегда идет нечетное, за ним снова четное и т.д.
Свойства N
Как и все другие множества, N обладают своими собственными, особыми свойствами. Рассмотрим свойства N ряда (не расширенного).
Внимание! Все вышеперечисленные неравенства действительны и в обратном направлении.
Как называются компоненты умножения

Для того, чтобы быстро и правильно умножать и уметь решать обратные задачи, необходимо знать компоненты умножения.
15.10=150. В данном выражении 15 и 10 являются множителями, а 150 – произведением.
Умножение обладает свойствами, которые необходимы при решении задач, уравнений и неравенств:
Например: 15.Х=150. Разделим произведение на известный множитель. 150:15=10. Сделаем проверку. 15.10=150. По такому принципу решаются даже сложные линейные уравнения (если упростить их).
Важно! Произведение может состоять не только из двух множителей. Например: 840=2.5.7.3.4
Что такое натуральные числа в математике?
Разряды и классы натуральных чисел
Вывод
Подведем итоги. N используются при счете или обозначении количества предметов. Ряд натуральных совокупностей цифр бесконечен, но он включает в себя только целые и положительные суммы разрядов и классов. Умножение тоже необходимо для того, чтобы считать предметы, а также для решения задач, уравнений и различных неравенств.
Это интересно! Легкие правила округления чисел после запятой
Действительные числа
Определение действительных чисел
Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —
Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —
Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:
Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.
Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.
Примеры действительных чисел:
Число нуль также является действительным числом, так как 0 — рациональное число.
Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.
При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.
Действительные числа на координатной прямой
Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Интересный факт: действительные числа заполняют каждую точку координатной прямой.
Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.
Представления действительных чисел
По определению действительными числами являются:
Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.
Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений
будут действительные числа.
Сравнение действительных чисел
Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:
Урок 9 Бесплатно Меньше или больше
Вы уже знаете, что такое натуральное число и как оно записывается.
Также Вам известно, что такое координатный луч.
Сегодня мы применим эти знания, чтобы сформулировать понятия “больше” и “меньше” для натуральных чисел, научимся отвечать на вопрос, как соотносятся два натуральных числа.
Узнаем, как сравнивать числа с помощью координатного луча, как сравнивать натуральные числа с одинаковым и разным количеством знаков, разберем понятие “сортировка” для чисел.
Определение
Вспомним, как выглядит натуральный ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9 …
Из двух натуральных чисел больше то, которое при счете называют позже.
Из двух натуральных чисел меньше то, которое при счете называют раньше.
Данное определение достаточно просто и понятно, посмотрим на примерах.
Например, как соотносятся 3 и 5?
Если мы посмотрим на натуральный ряд, то увидим, что 3 названо раньше, чем 5, следовательно, 3 меньше 5-ти.
Другой пример, как соотносятся числа 9 и 6?
Опять же, надо посмотреть на натуральный ряд, тогда можно увидеть, что 9 названо позже, чем 6, значит, 9 больше 6-ти.
Каждый раз писать словами “больше” или “меньше” может быть неудобно, поэтому удобно использовать знаки.
Знак “ ” читается как “больше”.
Таким образом, чтобы кратко записать, что 3 меньше 5-ти, достаточно написать “\(\mathbf<3 6>\)”.
Запись с использование знаком “больше” или “меньше” называют неравенством.
Довольно часто вопрос про соотношение двух чисел может ставится так: “какой знак должен стоять в неравенстве на месте пропуска”, а дальше идет неравенство с пропущенным знаком, например, такое: “4 _ 6”.
В данном случае надо ответить на вопрос, больше ли 4 6-ти или меньше, и поставить соответствующий знак.
Здесь первое число меньше второго и нужно поставить знак “ 0”, “2 > 0”, “3 > 0” и так далее для каждого натурального числа.
Пройти тест и получить оценку можно после входа или регистрации
Сравнение натуральных чисел: равно или не равно, больше или меньше?
Сравнение натуральных чисел между собой – тема данной статьи. Разберем сравнение двух натуральных чисел и изучим понятие равных и неравных натуральных чисел. Выясним большие и меньшие из двух чисел на примерах. Поговорим о натуральном ряде чисел и об их сравнении. Будут показаны результаты сравнений трех и более чисел.
Сравнение натуральных чисел
Рассмотрим это на примере. Когда на дереве имеется стая, состоящая из 7 птиц, а на другом из 5 десятка птиц, то стаи считаются разными, так как не похожи друг на друга. Отсюда можно делать вывод о том, что эта непохожесть и есть сравнение.
При сравнении натуральных чисел проводится такая проверка на похожесть.
Если считать, что под сравнением натуральных чисел подразумевают действие, то оно может привести к нескольким результатам:
Когда получаем неравенство, это значит, что одно из этих чисел больше или меньше другого, что и увеличивает диапазон использования натуральных чисел.
Рассмотрим определения равных и неравных чисел. Разберем, каким образом это определяется.
Равные и неравные натуральные числа
Рассмотрим определение равных и неравных чисел.
В случае, когда записи двух натуральных чисел одинаковы, их считают равными между собой. Когда записи имеют различия, тогда эти числа неравные.
Сравнение однозначных натуральных чисел
Если в записи имеются два натуральных числа со знаками « » и « > », тогда она называется неравенством. Неравенства могут быть верными и неверными.
Запись 4 7 – верная, а 3 > 9 – неверная.
Сравнение однозначного и многозначного натуральных чисел
Если принять за правило, что все однозначные числа меньше двухзначных, тогда получим:
Рассмотрим сравнения многозначных чисел.
Сравнение многозначных натуральных чисел
Рассмотрим сравнение двух неравных многозначных натуральных чисел с равным количеством знаков. Предварительно следует повторить раздел, изучающий разряды натурального числа и значение разряда.
В таком случае производится поразрядное сравнение, то есть слева направо. Меньшим считается число, которое имеет меньшее значение соответствующего разряда и наоборот.
Чтобы решить пример, нужно уяснить, что 0 всегда меньше любого натурального числа и что он равен самому себе. Число ноль относится к разряду натуральных чисел.
Сравнение многозначных натуральных чисел производится по-другому. Большим числом считают то, которое имеет меньшее количество знаков и наоборот.
Решение
Натуральный ряд чисел, нумерация, счет
Эта запись продолжается до бесконечности. Такая бесконечная последовательность чисел называется натуральным рядом чисел.
Существует еще один процесс – счет. Во время счета числа называются одно за другим, то есть таким образом, как они зафиксированы по ряду. Данный процесс применим для определения количества предметов.
Исли имеется определенное число предметов, но нам необходимо узнать количество, используем счет. Он производится, начиная с единицы. Если во время пересчета перекладывать предметы в кучу, то ее можно назвать натуральным рядом чисел. Последний предмет будет являться числом их количества. Когда процесс закончен, мы знаем их число, то есть предметы пересчитаны.
Во время счета меньше то натурально число, которое находится раньше и называется раньше. Применение нумерации используется для конкретного определения предмета, то есть присваивая ему определенный номер. Например, имеем некоторое количество предметов. На каждом из них зафиксируем их порядковый номер. Таким образом производится нумерация. Она применима для различения одинаковых предметов.
Натуральные числа на координатном луче
Для начала необходимо повторить определение координатного луча.
При просмотре слева направо видим штрихи, которые означают определенную последовательность чисел, начиная от 0 и до бесконечности. Эти штрихи называют точками. Точки, расположенные левее меньше точек, расположенных правее. Отсюда следует, что точка, имеющая меньшую координату на координатном луче, расположена левее точки с большей координатой.
Наименьшее и наибольшее натуральное число
Считается, что 1 – это наименьшее натуральное число из множества всех натуральных чисел. Все числа, расположенные правее него считаются больше предыдущего. Этот ряд бесконечен, поэтому нет наибольшего числа из этого множества чисел.
Двойные, тройные неравенства
Таким же образом выполняются тройные, четверные и так далее неравенства.
Необходимо быть внимательным при составлении двойных неравенств, так как можно произвести его неверно, что повлечет за собой неправильное решение задачи.