Что значит хвост трех саженей
 lsvsx
lsvsx
Всё совершенно иначе!
Истина где-то посередине. Так давайте подгребать к ней не теряя достоинства.
Наши Предки обладали такими знаниями, от которых сегодняшняя «цивилизация» Земли непередаваемо далека. Да, в это трудно поверить, а ещё труднее представить, но это именно так и есть. Доказательства в тексте ниже…
Нас всё время пытаются убедить, что Русь «образовалась» тысячу лет назад при крещении, что мы такие примитивные, «варвары, говорящие непонятно на каком языке…», и всё, чего мы достигли, всё это благодаря только более древним цивилизациям: египетской, греческой и европейской. К сожалению, эту точку зрения проводят в жизнь отечественные «горе-историки», придерживающиеся до сих пор норманнской и других прозападных теорий происхождения Руси. Нас убеждают, что и строить нас, опять-таки, научили греки, итальянцы и иже с ними.
Однако огромное количество фактов и проведённый анализ показал, что в древнерусском «Всемере» были заложены знания, использовавшиеся не только русскими зодчими, но и зодчими других народов. Эти знания несли в себе глубокую информацию о гармонии мироздании, отражённую в числах.
Полна загадок история Древней Руси. Но одно из самых загадочных её достижений – измерительная система, использовавшаяся при строительстве храмов и всех других сооружений. Сохранившиеся памятники архитектуры демонстрируют гармонию, как в эстетическом, так и архитектурном содержании. При этом утверждается, что-де церковная сажень имеет в основе древнеримские пассы, греческая – греческие оргии, великая сажень – шведский межевой локоть, а царская – египетский царский локоть… Иными словами, славянский народ якобы был не способен ввести единый измерительный инструмент и потому бессознательно собирал и использовал знания, наработанные соседними народами. С этих позиций даже предположение о возможности существования строгой пропорциональной системы древнерусских саженей представляется просто невероятным.
Однако видному архитектору А. Пилецкому удалось получить схему, названную им «Древнерусским Всемером», отображающую системную зависимость между саженями Древней Руси. Это своего рода числовая матрица, важнейшая особенность которой заключается в том, что она впервые показала глубинную суть древнерусских саженей, имеющих в основе золотую пропорцию!
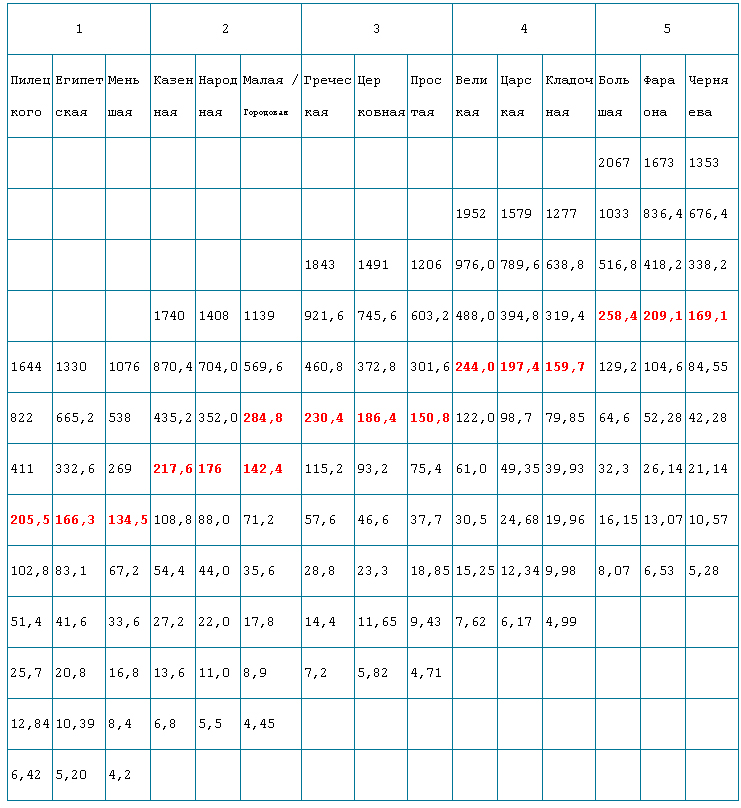
Известно, что на Руси основным измерительным инструментом была сажень. Их существовало несколько десятков. Наиболее распространенными были – городовая (284,8 см.), великая косая сажень (249,6 см.), великая (244,0 см.), греческая (230,4 см.), казённая (217,6 см.), косая сажень (216 см.), царская (197,4 см.), церковная (186,4 см.), морская сажень (183 см.), народная (176,0 см.), кладочная (159,7 см.), простая (150,8 см.), малая (142,4 см.) и другие (Черняев А.Ф. «Золото Древней Руси. Русская матрица – основа золотых пропорций». М., 1998 г.).
Причём, сажень не являлась директивным неизменяемым инструментом, любой мастер мог изобрести свою персональную сажень. Зодчий в своей практике, как правило, пользовался набором из трёх-пяти саженей. Для измерения длины, ширины и высоты пользовались разными саженями. При измерении или строительстве одного и того же объекта могли пользоваться разными, несоразмерными друг другу саженями. Но главное было в том, что эти сажени должны были придерживаться строгой пропорции, а фактически соразмерны пропорциям Земли (её расстояниям от её центра до полюсов, до экватора и т.д.): пропорции сооружения чётное число раз пропорциональны объёму Земли.
Мой комментарий: «Отсюда становится ясным изначальный смысл слова «С — ТРОИТЬ» — т.е. соединить в сооружении три меры (длины-ширины и высоты), определенными в разных системах отсчета.
В качестве основного инструмента, по мнению академика Б.А. Рыбакова, для расчёта и измерения при проектировании и строительстве на Руси пользовались «мерилом» (фото обломка Новгородского мерила см. ниже), представляющим собой два плотно складывающихся бруска с нанесёнными на их трёх гранях рисками, т.е. некое подобие логарифмической линейки (рис. 1). Такой инструмент был найден при раскопках в Новгороде. Числа, вероятно, остались на утраченной части облома. А потому методика применения мерила остаётся не совсем ясной…
На одном мериле три разные шкалы, и, по мнению академика Б.А.Рыбакова, это означает, что перед нами – расчётный архитектурный инструмент, аналогичный логарифмической линейке. А каждая его шкала, видимо, пропорциональна какой-то сажени. Он стал разбираться и выяснил: сумма длин клеток на каждой стороне мерила оказывается равной городовой сажени (284,8 см). Причём на мериле «укладывались» размеры всех 14 саженей «Всемера». Рыбаков восстанавливает новгородское мерило в виде стержня, содержащего элементы набора частей длин трёх саженей: мерной (маховой), великой (косой) и прямой (простой), но в необычном для древнерусских пропорций делении – каждая сажень делится на 21 элемент (рис. 2. Реконструкция мерила).
Поскольку при любом диаметре круга, когда диаметр делится на 21 часть, в самом круге с большой точностью будут укладываться 66 таких же отрезков. Это деление известно с древности, как отношение Архимеда в виде пропорции 22:7 = 3,1428, что и обусловливает возможность построения любой окружности с точностью до 0,05% и проведения операции перевода окружности и отрезка любой окружности (дуги) в линейные меры.
Конечно, мерилом могли пользоваться только посвящённые. При этом им нужно было знать, сколько и какие отрезки-клетки мерила сложить или вычесть, чтобы получить заданные пропорции или нужную сажень. В любом случае все размеры будущего сооружения подчинялись гармонии «золотого сечения». При строительстве культовых сооружений каждый его параметр измерялся тремя вариантами саженей.
Представим используемые сажени в виде убывающего ряда и найдём численные соотношения между ними, сведя их в Таблицу 1. Как видно из Таблицы 1, все сажени соотносятся друг с другом в соответствии с законами золотого сечения, золотого вурфа, через соответствующие коэффициенты 1,618 и 1,309. (смотреть таблицу 1). И лишь некоторые из группы саженей несколько «нарушают» общий порядок (1,102 вместо 1,059; 1,187=1,309:1,102 вместо 1,236; 1,362=1,102х1,236 вместо 1,309), при этом находясь в пределах матрицы, но в других рядах.
Поскольку гармоничность является одним из свойств золотого сечения, а число 2 – октава темперированной музыкальной гаммы и образуется малыми секундами, то было сделано предположение, что малая секунда, равная 2, соответствует коэффициенту 1,05946…, является шагом по вертикали русской матрицы и обеспечивает ей музыкальную гармоничную структуру.
Введение метра в качестве единицы измерения, нарушило эти пропорции и гармонию в сооружениях. Теперь в сооружениях все размеры в плане стали параллельными или перпендикулярными друг другу. Такие помещения – мертвы. В старых сооружениях этого нет, т.к. длина и ширина измерялись разными саженями, а это приводило к тому, что в плане сооружения нарушалась симметрия, и всюду имелись живительные углы наклона. При изменении положения в таком помещении создавалось ощущение оживления углов, и помещение на глазах как бы меняло свои размеры.
Дело в том, что в таком помещении нет негативно-скрытой – стоячей волны потока первичных материй («Неоднородная Вселенная»), выкачивающей из человека энергию. Здесь проявляется эффект полостных структур, который открыл В.С. Гребенников. В помещениях с такой структурой меняется мерность в местах сужения и происходит изменение плотности потока первичных материй – как в линзах поток света. Интенсивность потоков оказывает влияние на самочувствие человека. Это ещё раз подтверждает ту мысль, что наши предки сохранили часть ведических знаний, которыми обладали славяне до последней планетарной катастрофы.
Древний зодчий, как отмечает академик Международной академии информатизации при ООН А.Ф. Черняев, при проектировании сооружений ничего не вычислял, т.к. в этом не было необходимости.
Имея «Всемер», зодчий выбирал соизмеримость саженей по правилу групп, т.к. он знал, что только при следовании методике – канону – можно получить красивое сопряжение пропорций, гармонию. А пропорции не вычислялись, т.к. они изначально заложены в длины саженей (см. Табл. 1). Набор из нескольких саженей, выбранных по канону, всегда составляют пропорцию (1,618), кратную золотому числу. Причём, канон не зависел, ни от каких физических воздействий, в отличие от метра, длина эталона которого зависит от температуры и др. воздействий. Сажень в виде верёвки деформируется равномерно, поэтому пропорции остаются неизменными.
Все размеры саженей, кроме крайних, могут быть связаны, как показано ещё А.А. Пилецким, с габаритами человека следующей зависимостью:
В числителе – размер в положении с поднятой рукой, в знаменателе – рост человека.Очень маленький – 176 / 142,4
Маленький – 186,4 / 150,4
Ниже среднего – 197,4 / 159,7
Среднего – 205,5 / 166,3
Выше среднего – 217,6 / 176
Высокий – 230,4 / 186,4Очень высокий – 244 / 197,4
Здесь коэффициент, связывающий граничные значения в интервале соответствующего роста человека равен 1,236, например: 230,4/186,4=1,236.
На протяжении многих веков отсутствие единого стандарта не мешало, а более того – способствовало возведению великолепных, эстетически пропорциональных природе сооружений ещё и потому, что в древнерусской архитектуре все членения были трёхчастными.
Почленные части трёхчастного деления тела (вурфа) образуют систему взаимного пропорционирования и потому оказываются неразделимыми. Надо отметить, что, например, в живой природе, в биологических телах, в строении тела человека трёхчастное деление наблюдается постоянно. Например: пальцы рук и ног имеют трёхфаланговое строение, руки – трёхчленистое (плечо-предплечье-кисть: в 20 лет: 32,3-24,5-18,8 см), такое же ноги (бедро-голень-стопа: 45,4-37,5-27,0 см.); в масштабе размеров тела (в антропологии трёхчленность также различают: верхний отрезок – от макушки головы до основания шеи; средний отрезок, или туловище – от основания шеи до тазобедренного сочленения; нижний отрезок – от тазобедренного сочленения до конца пальцев ног: 25,3-51,8-109,9 см.). Численные соотношения между размерами тела, равные 1,309, называются золотым вурфом (Коробко В.И., Коробко Г.Н. «Золотая пропорция и человек». – М., 2002. 394 с., ISBN 5-93-93-130-5). Это можно видеть и в Табл. 1.
Вурфные пропорции позволяют выявить группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные – общность некоторого множества трёхчленных соотношений.
И если конструкция имеет вурфное отношение трёхчленного деления, то, как бы ни перемещался наблюдатель относительно неё, угол зрения А, В и т. д. всегда будет иметь одно и то же значение вурфа, и движущийся наблюдатель будет воспринимать постоянно меняющуюся, остающуюся эстетически совершенной, гармоничную конструкцию.
Во времена Петра I русскую казённую сажень испортили, изменив её длину на 4,3 см, и уложив в неё семь английских футов.
Факты подтверждают, что древнерусская мерная система сажени являлась общемировой. Мексиканские пирамиды, Вавилонская башня строились в соответствии с древнерусским «Всемером». Известный учёный Э.И. Кучеренко, специалист по древним инструментам и геральдике, выяснил во время экспедиции по самарскому краю в 1947-1948 годах, что жители некоторых здешних районов «помнили», как их далёкие предки строили знаменитые египетские пирамиды. О том же говорят, кстати, старожилы Полтавской, Брянской областей. Вычисления показывают: все помещения, и объекты комплекса пирамид в Гизе проектировались и возводились по мерным инструментам, полностью соответствующим тем единицам измерения, которые мы называем древнерусскими саженями. К примеру, в структуре параметров пирамиды Хеопса мы находим десять вариантов древнерусских саженей. Но и это не всё. Ещё более древние сооружения Египта – Осирион в Абидосе, нижний храм пирамиды Хафра и знаменитый большой Сфинкс – построены с применением того же измерительного комплекса. А возраст этих сооружений, как полагают некоторые исследователи, 10-15 тысяч лет. То есть наша русская система саженей имеет более чем почтенный возраст.
А в Горьковской области крестьяне замеряли вес стога сена, используя древнеегипетский способ замера. А в Полтавской области крестьяне производят счёт весьма странным образом, о котором выяснилось после расшифровки древнеегипетского папируса, что этот счёт использовался в древнем Египте. А как в тех же 40-х годах в Горьковской области замеряли вес стога сена? Сейчас всё просто: загрузил машину и на весы. А как быть, когда у тебя лишь телега и лошадь? Так вот, мужик снимал вожжи и перебрасывал их поперёк через стог. Потом опять перебросил, опять что-то прикинул, сложил что-то. И так, скажем, раз семь. А потом уверенно говорит: вес стога – полторы тонны. Его не надо было проверять. Всё точно. Откуда он взял такой способ взвешивания? А способ-то – «древнеегипетский»!
В 1927 году наша Академия наук расшифровала один из древнеегипетских папирусов. Оказалось, в нём был записан математический счёт умножения. В это же время из Полтавской области возвращается экспедиция, проводившая там археологические раскопки. Один из учёных, когда был постояльцем у местного крестьянина, обратил внимание, как тот считает. А хозяин избы считал весьма странным образом. И только потом, после расшифровки папируса, выяснилось, что крестьянин считал прямо-таки «по папирусу»! Откуда полтавский землепашец мог знать древнеегипетский счёт?
Кстати, в детстве мне приходилось видеть, как наш конюх, талыш по происхождению (юг Азербайджана, Ленкоранский район. У талышей (относящихся к иранской группе народов) в языке есть слова, корневая система которых совпадает с древнеславянской. Талыши даже антропологически отличаются от азербайджанцев и других народов, населяющих юг Азербайджана. Лингвистам всё это ещё предстоит исследовать), определял вес стога сена описанным выше способом. Случайности здесь явно исключены. Правда, у некоторых исследователей возникает мысль о том, что славяне могли позаимствовать разные сажени у разных народов. Однако это предположение опроверг видный архитектор А. Пилецкий, который получил схему, отображающую системную зависимость между саженями Древней Руси. Используя её, он пришёл к построению системы пропорций, которую он назвал «Древнерусским Всемером». Это своего рода числовая матрица (Рис. 3.). Она отражает органическую взаимосвязь всех саженей и их пропорциональность золотому сечению, что ещё раз доказывает, что древнерусская система саженей является изобретением славян, а не привнесено извне.
Таким образом, матрица «Всемера» численно охватывает и отражает гармонию всех явлений природы и устройства нашего мира, являясь следствием более фундаментальных законов природы.
Согласно проведённым М. Марутаевым исследованиям, он выделяет три закона гармонии («Гармония мироздания – закон Единого Целого». Ж. «Российский колокол». № 3, 2005, с. 136-169).
1. Закон качественной симметрии. Он означает деление целого пополам и отражает принцип дихотомии, т.е. зеркальной симметрии.
2. Закон нарушенной симметрии. Он оказался сущностью закона 1. Если закон 1 основан в частности, на связи геометрического (хг) и арифметического (ха) средних (а/в:(а+в)/а), то основой закона 2 является соотношение (хг*хг/ха), а это есть среднее гармоническое (хгар:(а-х)(х-в)=а/в). Определяя хгар между центрами Sk, симметричными относительно любого выбранного центра Sk (как чётной, так и нечётной степени SQRT(2)).
3. Закон золотого сечения, который вытекает из законов 1 и 2. Конечно, эти законы являются следствием более общих законов мироздания, но они численно показывают, что мир наш устроен по законам гармонии.
Эти законы проявляются во всех явлениях мира: генетике, музыке, астрономии, физике, поэзии, социологии и т.д.
Мы живём в мире, в котором пропорции окружающих нас произведений архитектуры принадлежат к случайным семействам, и человек оказывается в среде, пропорциональная структура которой по своей симметрии ему не свойственна.
Золотое сечение / золотая пропорция /.
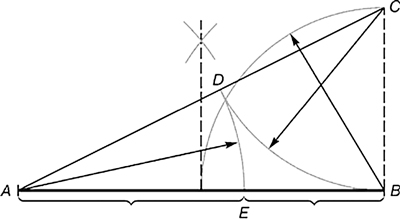
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Решение для числа Ф всего одно:
Ф=(1 + √5)/2 =1,6180339887498948482045868343656…
Ф-число иррациональное бесконечное. Обратная величина
Ф І = 2,6180339887498948482045868343656…
1,2,3,5,8,13,21,34, 55, 89. 377, 610, 987,1598, 2885.
Нетрудно заметить, что с увеличением порядковых номеров членов деление последующего члена на предыдущий всё более приближается к золотому числу Ф:
Итак, загадочное число Ф вычислено. Но зачем оно нам понадобилось? Оказывается, всё в природе, включая человека, создано согласно пропорциям золотого сечения. Мы любим красоту. Наше тело интуитивно чувствует золотую пропорцию. Всё, что нам кажется красивым, обладает свойствами золотого сечения. Будь то природный ландшафт, картина художника или тело человека. Почему это так, пока однозначного ответа нет.
За последние десятилетия многочисленными исследователями были установлены повсеместные проявления закона золотых пропорций от Космоса до Микромира. Во Вселенной все известные человечеству галактики существуют в форме спирали, соответствующей формуле золотого сечения. Русский астроном Бутусов в 1978 г. установил, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618.
Соотношения золотой пропорции исследователи находят в морфологической структуре растений, птиц, животных, человека. Закономерности золотой пропорции обнаруживаются и в организации неорганической природы, например, структура талой воды, практически соответствует треугольнику золотой пропорции. Таким образом, проявление принципа золотых пропорций наблюдается повсеместно в природе от бесконечно больших галактик до бесконечно малых клеток и атомов. Фигура человека, исследованная немецким исследователем проф. Цейзингом в 1855 г. явилась ярким примером золотых пропорций.
Дальше познакомимся с понятием вурфных соотношений.
Для блока, состоящего из трех элементов с длинами а, b, c вурфное отношение W(а, b, с) вычисляется по формуле:
При этом другой блок — с другими размерами и другими соотношениями элементов — а’, b’, с’ будет ему конформно симметричен, если величины их вурфов будут равны, т.е. если:
Путем преобразований такие блоки могут быть совмещены один с другим с полным совпадением всех их точек.
В процессе роста размеры частей тела человека и их соотношения все время меняются. Причём, эти изменения следуют принципам конформно-симметричных преобразований. Например, если взять соотношения стопы, голени и бедра в возрасте 1 года, 10 и 20 лет, то изменения выглядят так:
1:1,27:1,40; 1:1,34:1,55; 1:1,39:1,68.
Рост различных частей тела не протекает равномерно. Голень и бедро увеличиваются значительно больше, нежели стопа, пропорции тела человека все время меняются. Вурфные же соотношения для любого возраста вычисляются с одним и тем же значением:
W(1;1,27;1,40)=1,30; W(1;1,34;1,55)=1,30; W(1;1,39;1,68)=1,30
Вурфные пропорции позволяют, следовательно, выявить конформно-симметричные группы, иными словами, группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные — общность некоторого множества трехчленных соотношений.
Если пропорции окружающих нас произведений архитектуры, принадлежат к случайным группам, как в большинстве современных сооружений, то человек оказывается в среде, пропорциональная структура которой по своей симметрии ему не свойственна. Такая Среда, не обладающая ни одной из характеристических групп симметрии человека, чаще всего не воспринимается им, а нередко отвергается.
Оказалось, что все диагонали слева направо снизу вверх представляют собой ряды Фибоначчи и Золотую пропорцию одновременно. Для примера возьмём диагональ Народной сажени:
67,2+108,8=176,0 176/108,8=1,618 108,8/67,2=1,618
По строкам коэффициент везде 2/Ф = 2/1,618 = 1,236.
Но матрицы такой в Древней Руси, очевидно, не знали, и более логично им было выбрать соответствие саженей размерам человека. Если принять народную сажень равной росту зодчего, то каждый мог пропорционально ей вычислить остальные сажени. Делалось это разными очень простыми методами, вообще без применения цифр и вычислений (геометрически). Видимо, со временем для удобства приняли единую саженную систему, ориентированную на рост среднего человека – 176см, ему приравняли сажень народную.
Древнерусские сажени
ТАБЛИЦА САЖЕНЕЙ (в см)
По Черняеву. (Золотые сажени Древней Руси, 2007).
Соотношение сажени и ее элементов:
Локоть = ½ полсажени ( 1 /4 сажени)
Пядь = ½ локтя ( 1 /8 сажени)
Пясть = ½ пяди ( 1 /16 сажени)
Вершок = ½ пясти ( 1 /32 сажени)
А.Ф. Черняев
Золото Древней Руси, М., 1998
ЛОГИКА ДРЕВНИХ САЖЕНЕЙ
Возникают вопросы: А какими же методами производилось хранение измерительных инструментов в древности? Имеет ли смысл говорить об их точности? И не является ли требование точного измерения длины саженей логическим отголоском привычного использования стандартной единицы длины — метра? Ведь «хранение» это длилось тысячи лет со времен Древнего Египта, если не ранее [19]. К тому же никаких эталонов не найдено. Требовать от таких инструментов точности при отсутствии даже намеков на эталоны не приходится. И тем не менее.
Сооружения как Древней Руси, так и Древнего Египта своей соразмерностью, пропорциональностью и эстетической красотой, предназначенностью для облагораживающего воздействия на людей намного превосходят типовые и не типовые «коробки» XIX и XX вв. — детища очень точного стандартного метра.
Эта соразмерность и эстетическая красота сооружений — следствие особой, подвижной функции взаимосвязанного комплекса древнерусских саженей, заключающаяся в том, что их основное назначение — соизмерение, а потому они — не статические линейки, а остановленные длиною продолжающиеся динамические процессы.
Переведенные по длине, для облегчения пользования, в привычные для нас сантиметры, сажени, тем не менее, не обладают «настоящими» длинами. Сажени не являются измерительным инструментом и потому сами не имеют длины, хотя и применяются иногда для измерения. Как и тела не имеют размерности, так и сажени не обладают метричностью. Сажени — инструмент соизмерения, инструмент и система пропорционирования, поэтому их метрический модуль является бесконечным иррациональным числом, округленным до 4-го знака. А их диагональ слева направо снизу вверх есть не что иное как ряд золотой пропорции ( в данном случае речь идет о русской матрице коэффициентов – прим. мое О.С.).
В матрице А.А. Пилецкого сажени по этой причине являются абстрактным выражением бесконечного процесса, принявшего форму конечных отрезков. Каждая сажень имеет как бы свою внутреннюю единицу измерения длины, нам неизвестную, отличную от всех остальных длин, и обусловленную собственным процессом молекулярного деления.
Фактически каждая сажень является одним из тех иррациональных отрезков-процессов, которые получаются делением отрезка любой длины в крайнем и среднем отношениях. Складывая или деля сажени, мы складываем или делим не отрезки длины, а процессы, бесконечности, а результаты деления или сложения как бы представляем целыми и неделимыми отрезками. И потому вновь образовавшийся «отрезок» не является частью какого-то процесса, а представляет собой целое как новый самостоятельный процесс. В этом заключается основное качественное отличие саженей от метра. Метр — статическая измерительная единица, эталон, предназначенный для сопоставления с собой всех измеряемых тел. Сажень — соизмерительный процесс, обусловливающий нахождение соразмерности частей тел процессу, а следовательно, и самому телу. Метр фиксирует существующие пропорции, умертвляя их статичностью. Сажень соразмеряет пропорции процессом, оживляя их. Ибо все, что движется, соразмеренно живет.
Именно соразмерность определяет принципы разделения саженей на элементы. Являясь отрезком-процессом бесконечной длины, не отмеряемым ни к одному, ни к другому концу, сажень не может быть измерена никаким мерным инструментом.
Отрезок, имеющий один конец на бесконечности, обладает и другим концом, уходящим в бесконечность. И хотя для нас, для внешней системы, каждый из его концов конечен, и мы его определяем как конечный внешний измерительный инструмент, он остается для себя системой бесконечной, двигаясь в которой (если допустить, что нам в эту систему удалось попасть) от одного конца к другому никогда не дойти.
Разделить такой отрезок на две конечные части или отрезать от него, в его системе, отрезок конечной длины невозможно, ибо для такого отрезка не существует соизмеримого и неизменного эталонного элемента, кратного всему отрезку. Да и две разновеликие половинки — результат осуществленного разделения —сразу же изменят свои внутренние параметры. К тому же, как показывает деление в крайнем и среднем отношения, отрезок иррациональной длины не имеет места, находящегося точно по его центру, и деление его на 2 обусловливает появление двух иррациональных, как бы сопоставимых, но не соизмеримых по мерности отрезков-процессов.
А потому деление древних сажений-процессов возможно только на 2. Раздвоение саженей или их элементов приводит к появлению в качестве остатков только двух «бесконечно-конечных» длин. Растроение сажени, деление ее на 3, 5, 6, и т.д. частей невозможно, ибо создает условия для появления между бесконечными отрезками отрезков конечных, соизмеримых некоторому мерному инструменту, но не соразмерных, а следовательно, не являющихся процессами и не пригодных для соизмерения. Округление иррациональных раздвоенных отрезков в любых измерениях скрывает движение. Иррациональные числа, по С.Громову, — «не завершенные числа, как бы требующие постоянного довычисления», а потому динамические числа, и свойства их определяются динамической геометрией, представление о которой только начинают складываться в современной науке [9]. Кратко они сводятся к следующему.
В отличие от статической геометрии, в которой точка — геометрический объект, лишенный протяженности, а прямая, имея один ранг с точкой, представляет собой как бы слившиеся в длину точки и потому завершается с каждой стороны конечной точкой, в геометрии динамической точка есть сфера одного ранга, не имеющая центра, т.е имеющая радиус бесконечной длины, а прямая — слившиеся в одну цепочку точки другого, «меньшего» ранга. И завершается такая динамическая прямая пересечением границы предыдущей по рангу сферы-точки и устремлением по радиусу к ее отсутствующему центру, т. е. в бесконечность. Деление динамического отрезка сопровождается изменением в месте деления ранга «концевых» точек и превращением их в точки «большего» ранга, т.е. процессом движения по радиусу новых концов в бесконечность. Сложение вновь полученных, бесконечных отрезков не образует единого сдвоенного, как в статической геометрии, отрезка, а приводит к возникновению как бы составного, через точку другого ранга, отрезка. Так, диаметр любой окружности в динамической геометрии состоит, а не слагается, из двух бесконечных радиусов несоизмеримых с длиной образуемой ими окружности. Несоизмеримость проявляется всегда в виде трансцендентного числа при делении окружности на составной диаметр или на удвоенный радиус. Удвоение и есть составление двух бесконечностей в одну.
Эти процессы удвоения-раздвоения динамической геометрии положены, по-видимому, некоторой цивилизацией в основу системы древних саженей. Они определяют первую особенность изменения мерности соразмерных инструментов — получение отрезков меньшей длины последовательным делением их на 2. В матрице А.А. Пилецкого эта последовательность деления отображена рядом нисходящих под численной величиной каждой сажени чисел, образуемых последовательным делением ее на 2. Количество этих чисел, включая саму сажень, равно 6. Как было показано, они имеют следующие названия: сажень, полсажени, четверть сажени — локоть, восьмая часть сажени — поллоктя — пядь, шестнадцатая часть — полпяди или два вершка, или пясть, и тридцать вторая часть сажени — вершок или полпясти.
На вершке раздвоение заканчивается, хотя могло бы, как предполагал А.А. Пилецкий, и продолжаться бесконечно. Вершок является завершающим элементом, соразмерности. Он приобретает два функциональных назначения: с одной стороны, осуществляя функции соразмерности, а с другой, являясь измерительным инструментом. Он единственный среди элементов сажени может делиться на любое число, образуя измерительное частное, прибавление которого к любому элементу сажени превращает этот элемент из соизмерительного в измерительный, т.е. меняет его статус и качество с динамического на статическое, что делает невозможным участие его частей в процессе соизмерения. Ниже я попробую разобраться, чем обусловлено измерительное качество вершка, а пока отмечу, что существование шести раздвоенных элементов одной сажени является второй особенностью комплекса древних саженей.
ТАИНСТВО ЦЕРКОВНОГО ЗОДЧЕСТВА
Пропорции не вычислялись потому, что они изначально заложены в длины саженей, и набор из нескольких саженей, выбранных по канону, всегда составляет пропорцию, отображенную в матрице (т.е. кратную золотому числу).
Сажень для зодчего не становилась уставом. Не оставалась декретно неизменным инструментом. Он, вероятно, имел возможность, даже без понимания обусловливающей ее причины, изменять в пределах 1% ее длину, что, как уже говорилось, не влияет на пропорционирование, но «размывает» его границы, которые к тому же намеренно выполнялись более «расплывчатыми» (например, их орнаментами, фризами, кокошниками и т.д.). Возможность изменения длины — вторая составляющая наличия многих видов саженей на территории Руси (первая, как показано выше, — восстановление саженей без ориентации на единый эталон).
Сажень как скрытый процесс с удвоением длины изменяет свою динамику. Пропорции, отображаемые ею, становятся как бы подвижными. Динамика подвижных пропорций повергает истинного Мастера, мастера с большой буквы, на создание гармоничного объекта в сотворчестве с Богом. И чем большей духовностью обладает Мастер, чем тоньше его чувство возвышенного и возвышающего, тем более впечатляющим будет продукт этого сотворчества.
Особенно важным становилось для мастеров отображение потаенной пропорции в композиции духовных сооружений и в первую очередь церквей, соборов, храмов. Церковь как культовое сооружение является Храмом Божьим, Храмом Христа, объектом святости для верующих и даже неверующих. Святость — мерило церкви. Мерило же всегда выражается числом. Числом, за которым может скрываться качество, в том числе и значимость возводимого объекта.
Число Христа 7. Число священное, иными словами — сакральное. И качественная композиция сооружаемой церкви как храма Христа, как сооружения духовного в своей потаенной пропорции включала элементы сакральности, содержащие совмещенное количество сдвоенных мер: мирские, открытые для всех,
и потаенные, кратные 7. И включала так, что не посвященные в таинство культовых сооружений христианства не замечали ни сдвоенности, ни кратности. Так же, как не замечалось и то, что в разбиении церкви, имеющей высший статус святости, было задействовано не менее 7 саженей различной длины.
Эти правила были настолько законспирированы и с такой осторожностью соблюдались (это и обусловило, по-видимому, их потерю), что и сегодня, любуясь, например, Великой Печерской церковью в Киеве, церковью Вознесения в Коломенском или той же церквью Параскевы Пятницы в Новгороде (или их макетами), даже крупные архитекторы не догадываются о двойной мерной структуризации этих шедевров и о саженной сакральности их пропорций священному числу 7. (И здесь отмечается параллель с древнеегипетской сакральностью.)
ДРЕВНЕРУССКАЯ МЕТРОЛОГИЯ
ЕГИПЕТСКИХ ПИРАМИД
Пирамиды Египта, возведенные почти за 3000 лет до н.э., и сегодня остаются загадочными и по технологии своего возведения, и по тем знаниям, которыми владели строители пирамид. Одной из самых больших загадок построения пирамид является загадка размеров мерных инструментов, по которым производилось конструирование и возведение объектов Древнего Египта. Построение строжайше выверенных пирамид (практически точные углы 90°, отклонение всего на 2-3 см сторон основания при длине более 200 м, соблюдение до секунд углов наклона боковых сторон, сведение граней пирамид в одну точку на высоте более 100 м и т.д.) свидетельствует о наличии у строителей точных измерительных инструментов и хорошо отработанной методики пространственного измерения. Но каковы размеры этих инструментов? Какое пропорционирование в них заложено? Какова методика производства измерительных работ? До сих пор науке это неизвестно.
Большинство исследователей считают, что древнеегипетские архитекторы также пользовались единым мерным инструментом, длина которого, как они полагают, почти совпадала с длиной современного стандартного метра. Со временем его размеры будут уточнены. Нахождение этих размеров осложняется тем, что результаты измерения стандартным метром параметров древнейших объектов всегда оказываются дробными. И это при всеобщем убеждении, что древние египтяне не были знакомы с дробями.
Надо полагать, что зодчие Древнего Египта это понимали тоже. Тем более, что геометрия объектов и особенно измерительные инструменты, используемые на строительстве пирамид, показали бы, что к моменту начала возведения пирамид жрецы владели гармонией динамической геометрии, к пониманию которой, как уже говорилось, человечество только приближается [6]. А потому создается впечатление, вероятно, правдоподобное, что архитекторы фараона, возводившие пирамиды, преднамеренно скрывали параметры измерительных инструментов. Поскольку достигнуть понимания структуры полуразрушенных пирамид без знания гармонии использования измерительных инструментов, их породивших, невозможно. Другими словами: пока не будет найдена гармония пропорциональных взаимосвязей древних измерительных инструментов, невозможно даже приблизиться к разгадке тайн пирамид.
Можно отметить, что аналогичная дробность возникает при измерении метром параметров древнерусских сооружений. Но в этом случае известно, что возникающая дробность есть следствие использования в Древней Руси множества диспропорциональных друг другу и метру саженей.
То, что в течение столетий археологи и ученые не могут определить величину древнеегипетского аналога современного метра, скорее всего свидетельствует об отсутствии единого мерного инструмента и о возможном существовании в Египте некоторого подобия древнерусской системы измерительных инструментов. И встает вопрос: а не может ли оказаться так, что и в Древней Руси, и в Древнем Египте использовалась одна и та же метрологическая система?
Выше уже говорилось об одном из возможных подтверждений данной версии, отображенном на панелях Хеси-Ра. Однако изображение на панелях не может служить доказательством применимости древнерусских саженей, например, при строительстве пирамид. Этим доказательством может считаться только непосредственное подтверждение кратности размеров отдельных элементов тех же пирамид древнерусским соизмерительным инструментам и методам их применения, а пока этой соизмеримости не получено, данное предположение будет оставаться гипотетической версией.
Для проверки этой версии еще раз отметим особенности применения системы древнерусских саженей.
Основная особенность применения системы саженей заключается в том, что уменьшение мерности инструмента (получение измерительных стержней меньшего масштаба, чем сажень) производилось последовательным делением соответствующей сажени на 2 (раздвоение).
Вторая особенность: ни одно сооружение на Руси не строилось с применением только одного вида саженей. При замерах длины здания использовалась одна сажень, ширины — другая, высоты — третья. Внутренняя разбивка производилась четвертой саженью. А если возводился следующий этаж, то его высота определялась в зависимости от окружающего ландшафта еще одной саженью или комбинацией из сажени и ее элементов. Например: две сажени, полторы сажени, сажень с четвертью (с локтем) и т.д.
Третья особенность: все параметры объектов замерялись только целым, как бы квантованным, числом измерительных инструментов — саженей, локтей, вершков и т.д. Например, длина здания равнялась 6 саженям городовым по 284,8 см или 12 саженям малым по 142,4 см, что в измерении метром равно 17,088 м. Ширина равна четырем полуторным простым саженям по 150,8 х 1,5 = 2,262 см, а в измерении метром 9,048 м. Наконец, высота равна двум простым саженям по 150,8 см или 3,016 м.
Таким образом, параметры объектов, отмеренные целым числом саженей, всегда оказываются дробными при измерении стандартным метром. И, как уже отмечалось, эта особенность систематически фиксируется при замерах метром всех древнеегипетских сооружений. А потому можно повториться, что достигнуть понимания структуры полуразрушенных пирамид без знания гармонии измерительных инструментов, их породивших, невозможно.
Рассмотрим исходя из методов использования системы саженей возможность применения их для определения параметров комплекса пирамид в Гизе и других древнейших объектов. Поскольку названия древнеегипетских измерительных инструментов до нас не дошли, ниже употребляются названия их аналогов, принятых на Руси.
Результаты измерения саженями параметров пирамид в Гизе, отображенные в таблицах 10 — 12 с точностью до ± 5 см на сотни метров, подтверждают предположение о единстве древнерусской и древнеегипетской систем измерительных инструментов и позволяют сделать следующие выводы [19]:
— все параметры пирамид (высота h, боковая сторона а, диагональ основания d, боковое ребро b, апофема с) кратны целому числу различных саженей, оставаясь дробными в измерении метром;
— основной параметр пирамид — высота определяется для всех пирамид целыми десятками различных саженей 90, 60, 30, кратными сакральному числу 3;
— все параметры пирамид измеряются различными саженями;
— один или несколько параметров каждого объекта при приведении модуля числа саженей к одной цифре равен или кратен сакральному числу; вероятно, это значащие числа каждого параметра;
— наибольший наклон сторон имеет пирамида Хафра, как и наибольшее совпадение расчетных параметров с результатами обмера;
— в структуре параметров пирамид задействовано десять древнерусских саженей.
Из таблицы 7 следует, что в структуру пирамиды Хафра заложены параметры священного египетского треугольника 3:4:5:
107,8 : 35,93 = 3; 143,73 : 35,93 = 4; 179,66 : 35,93 = 5.
А этот треугольник ассоциируется по древнеегипетской мифологии с тройкой основных богов: малый катет — богиня плодородия Исида, большой катет, или высота пирамиды, — бог Осирис и гипотенуза (апофема) — их сын Гор, и отображает природную гармонию объекта.
Рассмотрим, совпадают ли параметры некоторых других объектов комплекса и их помещений с размерами саженей.
Наиболее сохранившийся храм ансамбля пирамид в Гизе — нижний храм пирамиды Хафра имеет квадратную форму со стороной основания 45 x 45 м и высоту 13 м. По-видимому, эти данные, как и многие другие, округлены и его истинные размеры составляют 45,24 х 45,24 м, или 30 саженей простых, а высота 13,05 м или 7 саженей церковных. Большая галерея пирамиды Хеопса имеет длину 47 м или 33 сажени малых, и высоту 8,5 м, что составляет б тех же саженей, а возможно, 3 сажени городовых, и действительная высота 8,54 м. Погребальная комната имеет размеры по обмеру: длина 10,5 м, ширина 5,2 м и высота 5,8 м.
Таблица 10. Пропорции пирамиды Хафра
 lsvsx
lsvsx