Что значит хотя бы один в теории вероятности

Вероятность появления хотя бы одного события

$P\left( A \right) = 1 — P\left( <\bar A>\right) = 1 — \cdot\cdot \ldots \cdot$

где q — вероятность наступления события, противоположного событию A

Пример 1
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,02 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
q₁ — вероятность неисправности первого платёжного автомата;
q₂ — вероятность неисправности второго платёжного автомата.
Искомая вероятность равна:

P=1–0.02·0.02=0.9996

Пример 2

Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.

Решение

А — «стрелки получат приз». Из условия задачи вероятность попадания равна р=0.3, следовательно вероятность их промаха

q=1–р=1–0,3=0,7

Отсюда искомая вероятность равна

P(A)=1–q 4 =1–0,7 4 =

=1–0,2401=0,7599

Пример 3
Вероятность попадания при одном выстреле в мишень 0,7. Найдите вероятность хотя бы одного попадания при 4 выстрелах.
Решение

q=1–р=1–0,7=0,3

P(A)=1–q 4 =1–0,3 4 =

=1–0,0081=0,9919

Пример 4
Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Решение
А — «устройство не работает»
A₁ — «отказал первый элемент»
A₂ — «отказал второй элемент»
Найдём вероятности безотказной работы независимых элементов
q₁=1-0,05=0,95,
q₂=1-0,08=0,92
Следовательно, вероятность того, что устройство не работает равна

==1-0,874=0,126

Пример 6

Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,5; 0,6

Решение

A₁=0.3, A₂=0.4, A₃=0.5, A₄=0.6 из условия задачи.
Воспользуемся формулой:

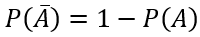
Находим соответствующие им вероятности

Р($\overline <>$) = 1 — 0,4 = 0,6

Р($\overline <>$) = 1 — 0,5 = 0,5

Р($\overline <>$) = 1-0,6 = 0,4

Из условия задачи события A₁, A₂, A₃ и A₄ независимы, следовательно получаем

Источник

Вероятность появления хотя бы одного события

Пусть в результате испытания могут появиться п событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны.

Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий А_1,А₂, А_п, независимых в совокупности, равна разности между единицей и произведением, вероятностей противоположных событий A₁А₂, А_п:

Частный случай. Если события A₁А₂, А„ имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий Р (Л) = 1 — q п (**)

Пример 1. Вероятности попадания в цель при стрельбе из трех орудий таковы: р₁ = 0,8; р_{2 =} 0,7;

р₃ = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события A₁(попадание первого орудия), А₂(попадание второго орудия) и А₃ (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям А₁ А₂ и А₃ (т.е. вероятности промахов), соответственно равны:

Искомая вероятность

Пример 2. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События «машина работает» и «машина не работает» (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: p + q = 1

Отсюда вероятность того, что машина в данный момент не работает, равна q = 1-p = 1—0,9 = 0,1.

Р (A) = 1 — q 4 = 1 — 0,1 4 = 0,9999.

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример 3. Вероятность того, что событие появится хотя бы один раз в трех независимых в совокупности испытаниях, равна 0,936. Найти вероятность появления события в одном испытании (предполагается, что во всех испытаниях вероятность появления события одна и та же).

Решение. Так как рассматриваемые события независимы в совокупности, то применима формула (**)

По условию, Р (А) = 0,936; п = 3. Следовательно,

0,936=1 — q 3 или q 3 = 1-0,936 = 0,064.

Отсюда q = 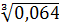= 0,4.

Искомая вероятность р = 1 — q = 1 — 0,4 = 0,6.

Источник

Решение задач с формулировкой «хотя бы один»

Поговорим о задачах, в которых встречается фраза «хотя бы один». Наверняка вы встречали такие задачи в домашних и контрольных работах, а теперь узнаете, как их решать. Сначала я расскажу об общем правиле, а потом рассмотрим частный случай независимых событий и схемы Бернулли, выпишем формулы и примеры для каждого.

Общая методика и примеры

Общая методика для решения задач, в которых встречается фраза «хотя бы один» такая:

А теперь разберем ее на примерах. Вперед!

Пример 1. В ящике находится 25 стандартных и 6 бракованных однотипных деталей. Какова вероятность того, что среди трёх наудачу выбранных деталей окажется хотя бы одна бракованная?

Действуем прямо по пунктам.
1. Записываем событие, вероятность которого надо найти прямо из условия задачи:
$A$ =(Из 3 выбранных деталей хотя бы одна бракованная).

Для первого примера запишем решение подробно, далее будем уже сокращать (а полные инструкции и калькуляторы вы найдете по ссылке выше).

4. Тогда искомая вероятность:

Пример 2. Из колоды в 36 карт берут наудачу 6 карт. Найти вероятность того, что среди взятых карт будут: хотя бы две пики.

4. Тогда искомая вероятность:

Пример 3. В урне 2 белых, 3 черных и 5 красных шаров. Три шара вынимают наугад. Найти вероятность того, что среди вынутых шаров хотя бы два будут разного цвета.

4. Искомая вероятность:

Частный случай. Независимые события

Идем дальше, и приходим к классу задач, где рассматривается несколько независимых событий (стрелки попадают, лампочки перегорают, машины заводятся, рабочие болеют с разной вероятностью каждый и т.п.) и нужно «найти вероятность наступления хотя бы одного события». В вариациях это может звучать так «найти вероятность, что хотя бы один стрелок из трех попадет в цель», «найти вероятность того, что хотя бы один автобус из двух вовремя приедет на вокзал», «найти вероятность, что хотя бы один элемент в устройстве из четырех элементов откажет за год» и т.д.

Если в примерах выше речь шла о применении формулы классической вероятности, здесь мы приходим к алгебре событий, используем формулы сложения и умножения вероятностей (небольшая теория тут).

Пример 4. Узел содержит две независимо работающие детали. Вероятности отказа деталей соответственно равны 0,05 и 0,08. Найти вероятность отказа узла, если для этого достаточно, чтобы отказала хотя бы одна деталь.

Действуем аналогично. Рассмотрим основное событие
$A$ =(Формула содержится хотя бы в одном справочнике). Введем независимые события:
$A_1$ = (Формула есть в первом справочнике),
$A_2$ = (Формула есть во втором справочнике),
$A_3$ = (Формула есть в третьем справочнике).

Пример 6. Рабочий обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что в течение смены первый станок потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвёртый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.

Думаю, вы уже уловили принцип решения, вопрос только в количестве событий, но и оно не оказывает влияния на сложность решения (в отличие от общих задач на сложение и умножение вероятностей). Только будьте внимательны, вероятности указаны для «потребует внимания», а вот вопрос задачи «хотя бы один станок НЕ потребует внимания». Вводить события нужно такие же, как и основное (в данном случае, с НЕ), чтобы пользоваться общей формулой (1).

Ответ: 0,982. Почти наверняка мастер будет отдыхать всю смену;)

Частный случай. Повторные испытания

Думаете, дальше будет сложнее? Напротив, случаи все более частные, решения и формулы все более простые.

Подробнее о схеме Бернулли можно прочитать в онлайн-учебнике, а также посмотреть статьи-калькуляторы о решении различных подтипов задач (о выстрелах, лотерейных билетах и т.п.). Ниже же будут разобраны задачи только с «хотя бы один».

Пример 7. Пусть вероятность того, что телевизор не потребует ремонта в течение гарантийного срока, равна 0,9. Найти вероятность того, что в течение гарантийного срока из 3 телевизоров хотя бы один не потребует ремонта.

Пример 8. Производится 5 независимых выстрелов по некоторой цели. Вероятность попадания при одном выстреле равна 0,8. Найти вероятность того, что будет хотя бы одно попадание.

Думаю, с применением формулы (2) все более чем ясно (не забудьте почитать и о других задачах, решаемых в рамках схемы Бернулли, ссылки были выше). А ниже я приведу чуть более сложную задачу. Такие задачи встречаются пореже, но и их способ решения надо усвоить. Поехали!

Пример 9. Производится n независимых опытов, в каждом из которых некоторое событие A появляется с вероятностью 0,7. Сколько нужно сделать опытов для того, чтобы с вероятностью 0,95 гарантировать хотя бы одно появление события A?

Округляя, получаем что нужно провести не менее 3 опытов.

Ответ: минимально нужно сделать 3 опыта.

Полезные ссылки

Источник

Учебник по теории вероятностей

1.4. Сложение и умножение вероятностей

События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается очевидно: А = В.

Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:

Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:

Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.

Примеры решений задач с событиями

Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим события: А – вынули белый шар из первого ящика,
;

— вынули черный шар из первого ящика,
;

В – белый шар из второго ящика,
;

— черный шар из второго ящика,
.

Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей
, .
Тогда искомая вероятность по теореме сложения будет
.

Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.

Пусть А – попадание первого стрелка, ;

В – попадание второго стрелка, .

Тогда — промах первого, ;

— промах второго, .

Найдем нужные вероятности.

а) АВ – двойное попадание,

б) – двойной промах, .

в) А+В – хотя бы одно попадание,

.

г) – одно попадание,

.

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

2. .

3.

Вероятность наступления хотя бы одного события

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий?

Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Примеры решений на эту тему

Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события (попадание первого орудия), (попадание второго орудия) и (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям , и (т. е. вероятности промахов), соответственно равны:

, ,

Искомая вероятность .

Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События «машина работает» и «машина не работает» (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице:

Отсюда вероятность того, что машина в данный момент не работает, равна

Искомая вероятность

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие «при n выстрелах стрелок попадает в цель хотя бы один раз». События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .

Приняв во внимание, что, по условию, (следовательно, ), получим

Прологарифмируем это неравенство по основанию 10:

Итак, , т.е. стрелок должен произвести не менее 5 выстрелов.

Источник

Теория вероятностей, формулы и примеры

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

У нас есть отличные курсы по математике для учеников с 1 по 11 классы — приглашаем на вводный урок!

Сложение и умножение вероятностей

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Источник