Что значит функциональная зависимость
Что значит функциональная зависимость
Можно сказать, что функциональные зависимости представляют собой связи типа «один ко многим», существующие внутри отношения.
Некоторые функциональные зависимости могут быть нежелательны.
Определение первой нормальной формы:
отношение находится в 1NF если значения всех его атрибутов атомарны.
Рассмотрим пример, заимствованный из уже упоминавшейся статьи Е.Ф.Кодда:
В базе данных отдела кадров предприятия необходимо хранить сведения о служащих, которые можно попытаться представить в отношении СЛУЖАЩИЙ(НОМЕР_СЛУЖАЩЕГО, ИМЯ, ДАТА_РОЖДЕНИЯ, ИСТОРИЯ_РАБОТЫ, ДЕТИ).
Их связь представлена на рис. 4.3.
Рис.4.3. Исходное отношение.
Для приведения исходного отношения СЛУЖАЩИЙ к первой нормальной форме необходимо декомпозировать его на четыре отношения, так как это показано на следующем рисунке:
Рис.4.4. Нормализованное множество отношений.
Здесь первичный ключ каждого отношения выделен синей рамкой, названия внешних ключей набраны шрифтом синего цвета. Напомним, что именно внешние ключи служат для представления функциональных зависимостей, существующих в исходном отношении. Эти функциональные зависимости обозначены линиями со стрелками.
неключевой атрибут функционально полно зависит от составного ключа если он функционально зависит от всего ключа в целом, но не находится в функциональной зависимости от какого-либо из входящих в него атрибутов.
Определение второй нормальной формы:
Отношение находится во 2НФ, если оно находится в 1НФ и каждый неключевой атрибут функционально полно зависит от ключа.
Отношение находится в 3НФ, если оно находится во 2НФ и каждый неключевой атрибут нетранзитивно зависит от первичного ключа.
Эта нормальная форма вводит дополнительное ограничение по сравнению с 3НФ.
Определение нормальной формы Бойса-Кодда:
Отношение находится в BCNF, если оно находится во 3НФ и в ней отсутствуют зависимости атрибутов первичного ключа от неключевых атрибутов.
Ситуация, когда отношение будет находится в 3NF, но не в BCNF, возникает при условии, что отношение имеет два (или более) возможных ключа, которые являются составными и имеют общий атрибут. Заметим, что на практике такая ситуация встречается достаточно редко, для всех прочих отношений 3NF и BCNF эквивалентны.
4.2.6. Многозначные зависимости и четвертая нормальная форма (4NF).
Многозначная зависимость является обобщением функциональной зависимости и рассматривает соответствия между множествами значений атрибутов.
Такие зависимости и называются многозначными и обозначаются как Нетрудно показать, что многозначные зависимости всегда образуют связанные пары, поэтому их часто обозначают Очевидно, что каждая функциональная зависимость является многозначной, но не каждая многозначная зависимость является функциональной.
Определение четвертой нормальной формы:
Отношение находится в 4NF если оно находится в BCNF и в нем отстутсвуют многозначные зависимости, не являющиеся функциональными зависимостями.
4.2.7. Зависимости по соединению и пятая нормальная форма (5NF).
Детально этот вопрос здесь мы не обсуждаем (полное изложение см. в книге К.Дейта), заметим лишь, что зависимость по соединению является обощением многозначной зависимости. Отношения, в которых имеются зависимости по соединению, не являющиеся одновременно ни многозначными, ни функциональными, также характеризуются аномалиями обновления. Поэтому, вводится понятие пятой нормальной формы.
Определение пятой нормальной формы:
Отношение находится в 5НФ тогда и только тогда, когда любая зависимость по соединению в нем определяется только его возможными ключами.
10) Функциональная зависимость СУБД
Что такое функциональная зависимость?
Функциональная зависимость (FD) определяет отношение одного атрибута к другому атрибуту в системе управления базами данных (СУБД). Функциональная зависимость помогает вам поддерживать качество данных в базе данных. Функциональная зависимость обозначена стрелкой →. Функциональная зависимость X от Y представлена X → Y. Функциональная зависимость играет жизненно важную роль, чтобы найти разницу между хорошим и плохим дизайном базы данных.
Пример:
| Количество сотрудников | Имя сотрудника | Зарплата | город |
| 1 | Dana | 50000 | Сан-Франциско |
| 2 | Фрэнсис | 38000 | Лондон |
| 3 | Эндрю | 25000 | Токио |
В этом примере, если мы знаем значение номера сотрудника, мы можем получить имя сотрудника, город, зарплату и т. Д. Таким образом, мы можем сказать, что город, имя сотрудника и зарплата функционально зависят от номера сотрудника.
В этом уроке вы узнаете:
Основные условия
Вот некоторые ключевые термины для функциональной зависимости:
| Основные условия | Описание |
| аксиома | Аксиомы — это набор правил вывода, используемых для определения всех функциональных зависимостей в реляционной базе данных. |
| декомпозиция | Это правило, которое предполагает, что если у вас есть таблица, которая содержит две сущности, определяемые одним и тем же первичным ключом, то вам следует рассмотреть возможность разбивки их на две разные таблицы. |
| зависимый | Он отображается в правой части диаграммы функциональной зависимости. |
| детерминанта | Он отображается в левой части диаграммы функциональной зависимости. |
| союз | Предполагается, что если две таблицы разделены, а PK одинаковы, вам следует рассмотреть возможность их размещения. все вместе |
Правила функциональных зависимостей
Ниже приведены три наиболее важных правила для функциональной зависимости:
Типы функциональных зависимостей
Многозначная зависимость в СУБД
Многозначная зависимость возникает в ситуации, когда в одной таблице имеется несколько независимых многозначных атрибутов. Многозначная зависимость — это полное ограничение между двумя наборами атрибутов в отношении. Это требует, чтобы определенные кортежи присутствовали в отношении.
Пример:
| Модель автомобиля | Maf_year | цвет |
| H001 | 2017 | металлический |
| H001 | 2017 | зеленый |
| H005 | 2018 | металлический |
| H005 | 2018 | синий |
| H010 | 2015 | металлический |
| H033 | 2012 | Серый |
В этом примере maf_year и color не зависят друг от друга, но зависят от car_model. В этом примере эти два столбца называются многозначными и зависят от car_model.
Эта зависимость может быть представлена так:
Тривиальная функциональная зависимость:
Тривиальная зависимость — это набор атрибутов, которые называются тривиальными, если набор атрибутов включен в этот атрибут.
BestProg
Нормализация. Функциональные зависимости атрибутов. Примеры. Построение схем функциональных зависимостей
Перед изучением данной темы рекомендуется ознакомиться с темой:
Содержание
Поиск на других ресурсах:
1. Понятие функциональной зависимости. Определение. Примеры
После того, как таблица приведена к первой нормальной форме 1НФ, нужно определить функциональную зависимость между атрибутами (полями, столбцами) таблицы. Это необходимо для обеспечения максимально-возможной рациональности в построении таблиц базы данных.
A → B
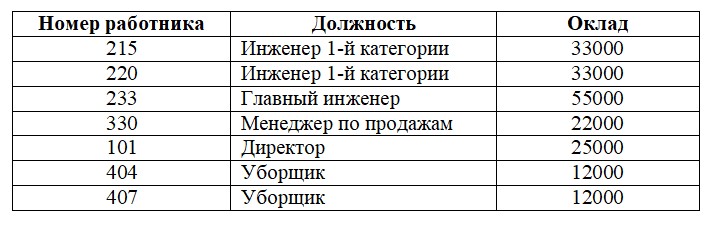
Пример 1. Пусть дано отношение, которое определяет должностные оклады работников некоторого предприятия.
Должность → Оклад
здесь Должность – детерминант, Оклад – зависимая часть.
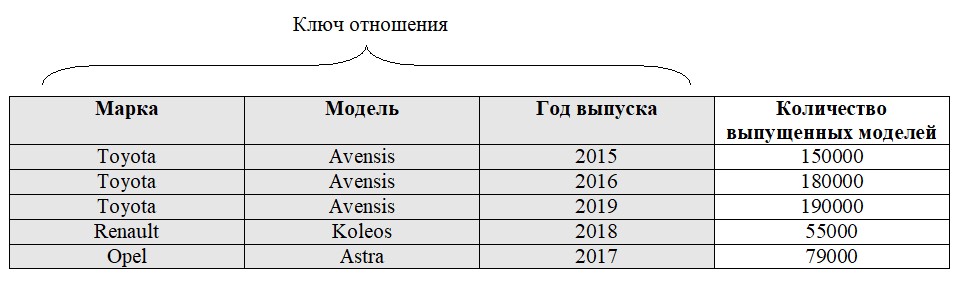
Пример 2. Демонстрируется зависимость атрибута от составного (композитного) ключа. На рисунке 1 изображена таблица выпуска различных моделей автомобилей в разные годы.
Рисунок 1. Функциональная зависимость атрибута « Количество выпущенных моделей » от ключа
2. Степени функциональной зависимости. Классификация
Различают следующие степени функциональной зависимости между атрибутами:
3. Частичная зависимость. Примеры
Пример 1. Пусть дана следующая таблица.
Поскольку атрибут Оклад зависит только от части ключа (атрибута Должность ) а не от всего ключа ( Номер работника — Должность ), то эта функциональная зависимость является частичной.
Рисунок 2 схематически отображает частичную зависимость.
Рисунок 2. Частичная зависимость атрибута Оклад от ключа отношения
Пример 2. Пусть дана таблица учета проведенных занятий в учебном заведении.
Рисунок 3. Частичная зависимость атрибута Дисциплина от ключа отношения
4. Полная функциональная зависимость. Примеры
Пример 1. Пусть дана база данных учета учебного процесса, таблица которой содержит атрибуты
Фрагмент таблицы базы данных следующий
Между этими атрибутами существует полная зависимость. Это означает, что за учебным годом можно определить курс, на котором учится студент. И, наоборот, по курсу обучения можно определить учебный год (при условии, что студент успешно сдал все сессии и не имеет задолженности по дисциплине «Организация баз данных и знаний» 🙂.
На схеме зависимостей такая связь обозначается следующим образом
Рисунок 4. Полная зависимость между атрибутами Год и Курс
Пример 2. Связь между идентификационным номером и именем гражданина. По имени гражданина можно определить идентификационный номер. И, наоборот, по идентификационному номеру можно определить имя гражданина.
5. Примеры транзитивной зависимости
Пример 1. Задана база данных, содержащая информацию о ходе учебного процесса в учебном заведении. В отношении (таблице) используются атрибуты (поля), имеющие транзитивные зависимости.
Между атрибутами Преподаватель и Группа существует транзитивная зависимость (рисунок 5).
Рисунок 5. Транзитивная зависимость между атрибутами Преподаватель и Группа
Поскольку, за каждой дисциплиной закреплен конкретный преподаватель, то между атрибутами Преподаватель и Группа существует транзитивная зависимость (Преподаватель преподает дисциплину в группе).
Пример 2. Пусть задана таблица начислений стипендии для студентов некоторой группы. Студенты могут учиться на госзаказе (бюджет) или по контракту.
От студента зависит вид договора на обучение: бюджет или контракт. Поэтому возникает функциональная зависимость между атрибутами Студент и Вид договора (рисунок 6).
Рисунок 6. Функциональная зависимость между атрибутами Студент и Вид договора
Вид договора влияет на размер стипендии. Если студент учится по контракту, то стипендия не начисляется. По размеру стипендии нельзя определить вид договора, поскольку студент может учиться на бюджете и не получать стипендию в связи с плохой успеваемостью. Поэтому, между атрибутами Вид договора и Стипендия существует следующая функциональная зависимость (рисунок 7).
Рисунок 7. Функциональная зависимость между атрибутами Вид договора и Стипендия
Значит между атрибутами Студент и Стипендия существует транзитивная зависимость (рисунок 8).
Рисунок 8. Транзитивная зависимость между атрибутами Студент и Стипендия
6. Примеры многозначной зависимости
Пример 1. В учебном заведении преподаватель может преподавать не одну а несколько родственных дисциплин.
Пример 2. Задана таблица стоимости новых автомобилей.
Между атрибутами Марка и Модель существует многозначная зависимость. Это объясняется тем, что для одной марки (Renault) может существовать несколько значений моделей (Logan, Megane, Koleos).
7. Задача. Построить схему функциональных зависимостей между атрибутами отношения
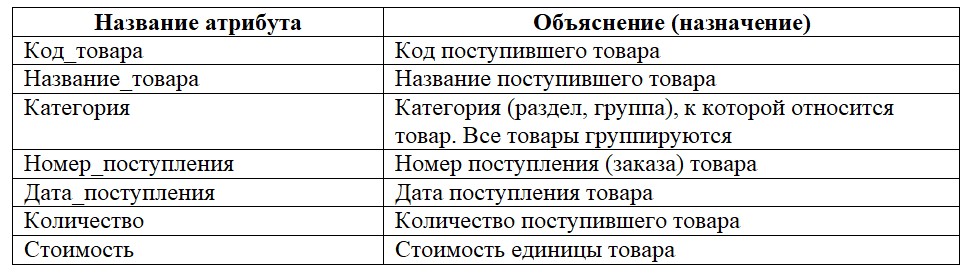
Условие задачи. Задана таблица базы данных «Учет товаров в автомагазине», которая приведена к первой нормальной форме 1НФ. Таблица определяет товары, поступающие на склад и имеет следующую структуру
Нужно построить схему зависимостей между атрибутами.
Решение. Схема зависимостей между атрибутами таблицы учета поступивших товаров на складе изображена на рисунке 9.
Рисунок 9. Схема зависимостей между атрибутами
8. Задача. Построить схему функциональных зависимостей между атрибутами отношения
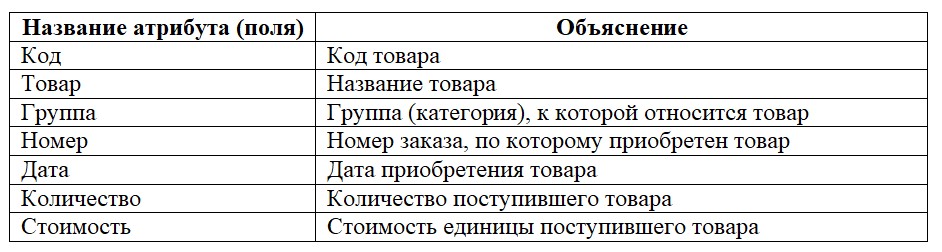
Задано таблицу базы данных магазина, которая отображает учет автозапчастей (товаров). Структура таблицы следующая
Рисунок 10. Схема функциональных зависимостей. Учет автозапчастей в магазине
9. Понятие независимых атрибутов. Примеры
Между отдельными атрибутами базы данных могут отсутствовать какие-либо функциональные зависимости. Такие атрибуты называются независимыми друг от друга.
Пример. Задана таблица с данными о преподавателе.
В вышеприведенной таблице нет функциональной зависимости между следующими атрибутами:
Введение в функциональные зависимости
В этой статье мы поговорим о функциональных зависимостях в базах данных — что это такое, где применяются и какие алгоритмы существуют для их поиска.
Рассматривать функциональные зависимости мы будем в контексте реляционных баз данных. Если говорить совсем грубо, то в таких базах данных информациях хранится в виде таблиц. Далее мы используем приближенные понятия, которые в строгой реляционной теории не являются взаимозаменяемыми: саму таблицу будем называть отношением, столбцы — атрибутами (их множество — схемой отношения), а набор значений строки на подмножестве атрибутов — кортежем.
Например, в таблице выше, (Benson, M, M organ) является кортежем по атрибутам (Пациент, Пол, Доктор).
Более формально это записывается в следующем виде: [Пациент, Пол, Доктор] = (Benson, M, M organ).
Теперь мы можем ввести понятие функциональной зависимости (ФЗ):
Определение 1. Отношение R удовлетворяет ФЗ X → Y (где X, Y ⊆ R) тогда и только тогда, когда для любых кортежей ,
∈ R выполняется: если
[X] =
[X], то
[Y ] =
[Y ]. В таком случае говорят, что X (детерминант, или определяющее множество атрибутов) функционально определяет Y (зависимое множество).
Иными словами, наличие ФЗ X → Y означает, что если мы имеем два кортежа в R и они совпадают по атрибутам X, то они будут совпадать и по атрибутам Y.
А теперь по порядку. Рассмотрим атрибуты Пациент и Пол для которых хотим узнать, есть ли между ними зависимости или нет. Для такого множества атрибутов могут существовать следующие зависимости:
Таким образом, функциональные зависимости позволяют определить имеющиеся связи между множествами атрибутов таблицы. Отсюда и впредь мы будем рассматривать наиболее интересные связи, а точнее такие X → Y, что они являются:
Посчитаем ошибку для Доктор → Пациент из примера выше. Имеем два кортежа, значения которых разнятся на атрибуте Пациент, но совпадают на Докторе: [Доктор, Пациент] = (Robin, Ellis) и
[Доктор, Пациент] = (Robin, Graham). Следуя определению ошибки, мы должны учитывать все конфликтующие пары, а значит таковых будет две: (
,
) и ее инверсия (
,
). Подставим в формулу и получим:
А теперь попытаемся ответить на вопрос: «А зачем оно все?». На самом деле, ФЗ бывают разные. Первый тип — это такие зависимости, которые определяются администратором на этапе проектирования базы данных. Их обычно немного, они строгие, а основное применение — нормализация данных и дизайн схемы отношения.
Второй тип — зависимости, представляющие «скрытые» данные и ранее неизвестные связи между атрибутами. То есть о таких зависимостях не думали в момент проектирования и их находят уже для имеющегося набора данных, чтобы потом на основе множества выявленных ФЗ сделать какие-либо выводы о хранимой информации. Как раз с такими зависимостями мы и работаем. Ими занимается целая область дата майнинга с различными техниками поиска и построенными на их основе алгоритмами. Давайте разбираться, чем могут быть полезны найденные функциональные зависимости (точные или приближенные) в каких-либо данных.
Сегодня среди основных областей применения зависимостей выделяют очистку данных. Она подразумевает разработку процессов выявления «грязных данных» с последующим их исправлением. Яркими представителями «грязных данных» являются дубликаты, ошибки в данных или опечатки, пропущенные значения, устаревшие данные, лишние пробелы и тому подобное.
Пример ошибки в данных:
Пример дубликатов в данных:
Например, мы имеем таблицу и набор ФЗ, которые должны выполняться. Очистка данных в данном случае предполагает изменить данные таким образом, чтобы ФЗ стали верны. При этом число модификаций должно быть минимально (для данной процедуры существуют свои алгоритмы, на которых мы не будем сосредотачивать внимание в данной статье). Ниже приведен пример такого преобразования данных. Слева исходное отношение, в котором, очевидно, не выполняются необходимые ФЗ (красным цветом выделен пример нарушения одной из ФЗ). Справа представлено обновленное отношение, в котором зеленые ячейки показывают измененные значения. После проведения такой процедуры необходимые зависимости стали удерживаться.
Другой популярной областью применения является дизайн базы данных. Здесь стоит напомнить про нормальные формы и нормализацию. Нормализация — это процесс приведения отношения в соответствие некоторому набору требований, каждый из которых определяется нормальной формой по-своему. Расписывать требования различных нормальных форм мы не станем (это делается в любой книге по курсу БД для начинающих), а лишь заметим, что каждая из них по-своему использует концепцию функциональных зависимостей. Ведь ФЗ по своей сути являются ограничениями целостности, которые учитываются при проектировании базы данных (в контексте этой задачи ФЗ иногда называют суперключами).
Рассмотрим их применение для четырех нормальных форм на картинке ниже. Напомним, что нормальная форма Бойса-Кодда является более строгой, чем третья форма, но при этом менее строгой, чем четвертая. Последнюю пока не рассматриваем, поскольку для ее постановки нужно понимание многозначных зависимостей, которые в данной статье нам не интересны.



Еще одной областью, в которой зависимости нашли свое применение, является понижение размерности пространства признаков в таких задачах как построение наивного байесовского классификатора, выделение значимых признаков и репараметризация регрессионной модели. В оригинальных статьях эта задача называется определением избыточных признаков (feature redundancy) и релевантных (feature relevancy) [5, 6], и решается она с активным использованием концепций баз данных. С появлением таких работ мы можем говорить, что сегодня наблюдается запрос на решения, позволяющие объединить базу данных, аналитику и реализацию вышеперечисленных проблем оптимизации в один инструмент [7, 8, 9].
Для поиска ФЗ в наборе данных существует множество алгоритмов (как современных, так и не очень).Такие алгоритмы можно разделить на три группы:
Подробнее о данной классификации можно почитать [4]. Ниже представлены примеры алгоритмов на каждый из типов:
В настоящее время появляются новые алгоритмы, которые сочетают в себе сразу несколько подходов к поиску функциональных зависимостей. Примерами таких алгоритмов являются Pyro [2] и HyFD [3]. Разбор их работы предполагается в следующих статьях данного цикла. В этой статье мы лишь разберем основные понятия и лемму, которые необходимы для понимания техник выявления зависимостей.
Начнем с простого — difference- и agree-set, используемые во втором типе алгоритмов. Difference-set представляет собой множество кортежей, которые не совпадают по значениям, а agree-set наоборот — кортежи, совпадающие по значениям. Стоить отметить, что в данном случае мы рассматриваем только левую часть зависимости.
Также важным понятием, которое встречалось выше, является алгебраическая решетка. Так как многие современные алгоритмы оперируют данным понятием, нам нужно иметь представление о том, что это такое.
Для того чтобы ввести понятие решетки, необходимо определение частично упорядоченного множества (или partially ordered set, сокращенно — poset).
В качестве простейшего примера частично упорядоченного множества можно взять множество всех натуральных чисел N с обычным отношением порядка ⩽. Нетрудно проверить, что все необходимые аксиомы выполняются.
Более содержательный пример. Рассмотрим множество всех подмножеств <1, 2, 3>, упорядоченное отношением включения ⊆. Действительно, это отношение удовлетворяет всем условиям частичного порядка, поэтому ⟨P (<1, 2, 3>), ⊆⟩ — частично упорядоченное множество. На рисунке ниже изображена структура этого множества: если из одного элемента можно дойти по стрелочкам до другого элемента, то они находятся в отношении порядка.
Нам потребуются еще два простых определения из области математики — супремум (supremum) и инфимум (infimum).
Определение 3. Пусть ⟨S, ⩽⟩ — частично упорядоченное множество, A ⊆ S. Верхняя граница A — это такой элемент u ∈ S, что ∀x ∈ A: x ⩽ u. Пусть U — множество всех верхних границ A. Если в U существует наименьший элемент, тогда он называется супремумом и обозначается как sup A.
Аналогично вводится понятие точной нижней границы.
Определение 4. Пусть ⟨S, ⩽⟩ — частично упорядоченное множество, A ⊆ S. Нижняя граница A — это такой элемент l ∈ S, что ∀x ∈ A: l ⩽ x. Пусть L — множество всех нижних границ A. Если в L существует наибольший элемент, тогда он называется инфимумом и обозначается как inf A.
Рассмотрим в качестве примера приведенное выше частично упорядоченное множество ⟨P (<1, 2, 3>), ⊆⟩ и найдем в нем супремум и инфимум:
Теперь можно сформулировать определение алгебраической решетки.
Определение 5. Пусть ⟨P, ⩽⟩ — частично упорядоченное множество, такое что всякое двухэлементное подмножество имеет точные верхнюю и нижнюю границы. Тогда P называется алгебраической решеткой. При этом sup
Проверим, что наш рабочий пример ⟨P (<1, 2, 3>), ⊆⟩ является решеткой. Действительно, для всяких a, b ∈ P (<1, 2, 3>), a∨b = a∪b, а a∧b = a∩b. Например, рассмотрим множества <1, 2>и <1, 3>и найдем их инфимум и супремум. Если мы их пересечем, то получим множество <1>, которое и будет являться инфимумом. Супремум же получим их объединением — <1, 2, 3>.
В алгоритмах выявления ФЗ пространство поиска зачастую представляется в форме решетки, где множества из одного элемента (читай первый уровень решетки поиска, где левая часть зависимостей состоит из одного атрибута) являют собой каждый атрибут исходного отношения.
В начале рассматриваются зависимости вида ∅ → Одиночный атрибут. Данный шаг позволяет определить, какие атрибуты являются первичными ключами (для таких атрибутов не бывает детерминантов, а потому левая часть пуста). Далее такие алгоритмы двигаются по решетке вверх. При этом стоит отметить, что решетку можно обходить не всю, то есть если на вход передать желаемый максимальный размер левой части, то дальше уровня с таким размером алгоритм идти не будет.
На рисунке ниже показано, как можно использовать алгебраическую решетку в задаче поиска ФЗ. Здесь каждое ребро (X, XY) представляет собой зависимость X → Y. Например, мы прошли первый уровень и знаем, что удерживается зависимость A → B (отобразим это зеленой связью между вершинами A и B). Значит далее, когда будем продвигаться по решетке вверх, мы можем не проверять зависимость A, C → B, потому что она будет уже не минимальной. Аналогично мы бы не стали ее проверять, если бы удерживалась зависимость C → B.

Кроме того, как правило, все современные алгоритмы по поиску ФЗ используют такую структуру данных, как партиция (в первоисточнике — stripped partition [1]). Формальное определение партиции выглядит следующим образом:
Определение 6. Пусть X ⊆ R — набор атрибутов для отношения r. Кластер представляет собой набор индексов кортежей из r, которые имеют одинаковое значение для X, то есть c(t) =
1\>$» data-tex=»display»/>
Простыми словами, партиция для атрибута X представляет собой набор списков, где каждый список содержит номера строк с одинаковыми значениями для X. В современной литературе структура, представляющая партиции, называется position list index (PLI). Кластеры единичной длины исключаются в целях сжатия PLI, потому что это кластеры, содержащие лишь номер записи с уникальным значением, которое всегда будет легко установить.
Рассмотрим пример. Вернемся все к той же таблице с пациентами и построим партиции для столбцов Пациент и Пол (слева появился новый столбец, в котором отмечены номера строк таблицы):
При этом, согласно определению, партиция для столбца Пациент на самом деле будет пустая, так как одиночные кластеры исключаются из партиции.
Партиции можно получать по нескольким атрибутам. И для этого существует два пути: пройдясь по таблице, построить партицию сразу по всем необходимым атрибутам, или же построить ее с помощью операции пересечения партиций по подмножеству атрибутов. Алгоритмы поиска ФЗ используют второй вариант.
Простыми словами, чтобы, например, получить партицию по столбцам ABC, можно взять партиции для AC и B (или любой другой набор непересекающихся подмножеств) и пересечь их между собой. Операция пересечения двух партиций выделяет кластеры наибольшей длины, общие для обеих партиций.
Давайте рассмотрим пример:
В первом случае мы получили пустую партицию. Если присмотреться к таблице, то действительно, одинаковых значений по двум атрибутам там нет. Если же мы немного модифицируем таблицу (случай справа), то уже получим непустое пересечение. При этом строки 1 и 2 и правда содержат одинаковые значения по атрибутам Пол и Доктор.
Далее нам понадобится такое понятие, как размер партиции. Формально:
1\>|$» data-tex=»display»/>
Проще говоря, размер партиции представляет собой количество кластеров, входящих в партицию (помним, что единичные кластеры в партицию не входят!):
Теперь мы можем определить одну из ключевых лемм, которая для заданных партиций позволяет установить, удерживается зависимость или нет:
Лемма 1. Зависимость A, B → C удерживается, если и только если
Согласно лемме, для определения, удерживается ли зависимость, необходимо выполнить четыре шага:



В данной статье мы разобрали такие понятия, как функциональная зависимость, приближенная функциональная зависимость, рассмотрели, где они применяются, а также какие алгоритмы поиска ФЗ существуют. Также мы подробно разобрали базовые, но важные понятия, активно используемые в современных алгоритмах по поиску ФЗ.
Ссылки на литературу: