Что значит через каждые две точки

Что значит через каждые две точки

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Плоскость, прямая линия, луч

Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Обозначение прямой

Например, на рисунке 1 обозначены такие прямые:

Рис. 1 Обозначение прямой линии

Рис. 2 Обозначение прямой с несколькими точками

Некоторые свойства прямой

Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

Рис. 5 Пересечение прямых

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

Луч имеет второе название – полупрямая.

Рис. 8 Дополнительные друг другу и совпадающие лучи

На рисунке 8 видно, что:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 22

Источник

Некоторые следствия из аксиом стереометрии

Урок 3. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Некоторые следствия из аксиом стереометрии»

На прошлом уроке мы с вами познакомились с аксиомами стереометрии. Давайте еще раз повторим их.

Первая аксиома звучит так: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Вторая аксиома звучит так: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Третья аксиома звучит так: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Сегодня на уроке мы сформулируем и докажем некоторые следствия из этих аксиом. По аналогии с аксиомами следствия мы будем обозначать заглавной буквой С с нижним индексом.

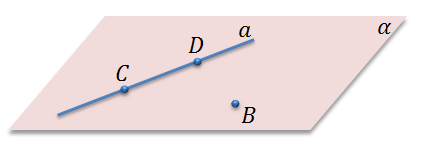
Итак, первое следствие звучит так: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Докажем это. Рассмотрим прямую a и не лежащую на ней точку B. Нам необходимо доказать, что через прямую a и точку B проходит плоскость. Отметим на прямой a две точки C и D. Точки B, C, D не лежат на одной прямой, поэтому согласно первой аксиоме, (а именно, тому что через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна) через эти точки проходит некоторая плоскость α. Поскольку точки C и D прямой a лежат в плоскости, то по второй аксиоме (если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости) вся прямая a лежит в плоскости α.

Теперь давайте докажем единственность этой плоскости. Любая плоскость, которая проходит через прямую a и точку B проходит через точки B, C, D. То есть она совпадает с плоскостью α, поскольку по первой аксиоме, плоскость, которая проходит через три точки, не лежащие на одной прямой – единственная.

Теперь давайте сформулируем и докажем второе следствие.

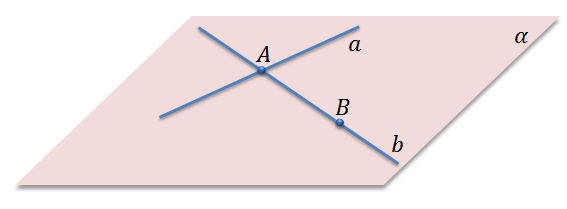
Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Рассмотрим прямые a и b, которые пересекаются в точке А. Тогда нам необходимо доказать, что через эти прямые проходит плоскость, и притом только одна.

Отметим на прямой b точку B, не совпадающую с точкой А. Тогда из первого следствия, через прямую a и точку B можно провести плоскость α. Так как точки А и B прямой b лежат в плоскости α, то по второй аксиоме мы получим, что вся прямая b лежит в плоскости α. Поскольку через прямую и не лежащую на ней точку можно провести только одну плоскость, то значит, любая плоскость, проходящая через прямые a и b совпадает с плоскостью α.

Таким образом, наша теорема доказана.

Решим несколько задач.

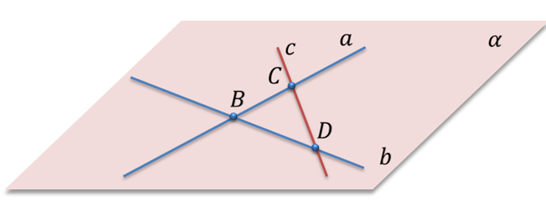
Задача. Две прямые пересекаются в точке . Доказать, что все прямые, которые пересекают данные прямые и не проходят через точку , лежат в одной плоскости.

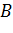
По второму следствию из аксиом стереометрии через две пересекающиеся прямые проходит плоскость, и притом только одна. Значит, через данные прямые проведем плоскость альфа.

Проведем прямую, которая будет пересекать прямые, но не проходит через точку B. Эта прямая с каждой из данных прямых имеет по одной общей точке. Эти точки принадлежат построенной плоскости, поскольку прямые принадлежат этой плоскости. Получаем, что две точки прямой принадлежат плоскости, значит, по второй аксиоме, вся прямая лежит в этой же плоскости. Поскольку прямую мы проводили произвольно, то, очевидно, что каждая из прямых, которые будут пересекать исходные прямые будет лежать в этой же плоскости, что и требовалось доказать.

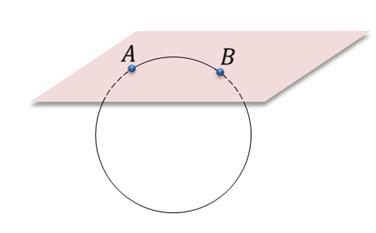
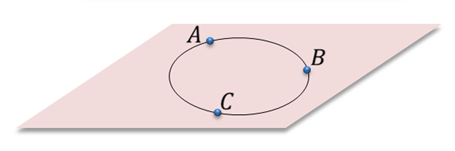
Задача. Верно ли утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?

Первое утверждение неверно, так как окружность и плоскость имеют две общие точки, если они пересекаются. То есть окружность не лежит в плоскости, а только пересекает ее.

Перейдем ко второму утверждению. По первой аксиоме через три точки, не лежащих на одной прямой можно провести плоскость и притом только одну. Точки окружности не могут лежать на одной прямой, поэтому проведем через них плоскость. Очевидно, что эти точки лежат в плоскости окружности, но поскольку аксиома говорит о том, что такая плоскость единственная, значит, окружность будет принадлежать этой плоскости. То есть второе утверждение верно.

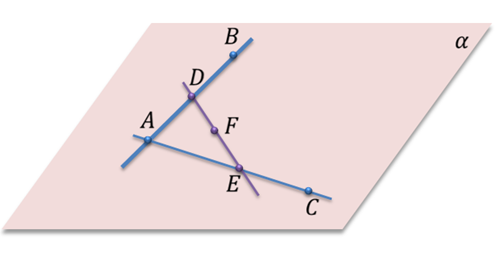
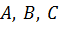
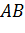
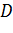
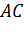
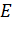
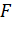
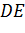
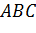
Задача. Пусть точки не лежат на одной прямой. Отметим на прямой точку , а на прямой – точку . Доказать, что точка прямой лежит в плоскости .

По первой аксиоме через точки А, B, C проведем плоскость α. Так как прямая АB лежит в плоскости α, значит, точка D лежит в плоскости α. Аналогично, поскольку прямая АC лежит в плоскости α, то и точка Е лежит в плоскости α. Получаем, что две точки прямой DE лежат в плоскости α. Применим вторую аксиому и получим, что вся прямая DE лежит в плоскости α. Тогда точка F прямой DE тоже лежит в плоскости α. Что и требовалось доказать.

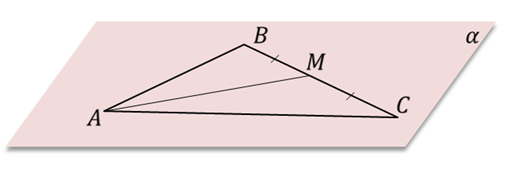
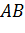
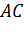
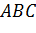
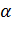
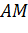
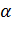
Задача. Пусть стороны и треугольника лежат в плоскости . Доказать, что и медиана лежит в плоскости .

Поскольку стороны AB и АC лежат в плоскости α, значит, точки B и C лежат в этой плоскости, то есть, по второй аксиоме, сторона BC тоже лежит в этой плоскости. Точка M лежит на прямой BC, значит, она лежит в плоскости α, что и требовалось доказать.

Подведем итоги урока. Итак, сегодня на уроке мы повторили аксиомы стереометрии, сформулировали и доказали некоторые следствия из аксиом и рассмотрели задачи, на использование аксиом и следствий из них.

Источник