Что означают вертикальные скобки в алгебре
Угловые скобки
Ско́бки — па́рные знаки, используемые в различных областях.
Используются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||.
В математике, физике, химии и др. используются при написании формул.
Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂.
Содержание
Круглые скобки
Используются в математике для задания приоритета математических и логических операций. Например, (2+3)·4 означает, что надо сначала сложить 2 и 3, а затем сумму умножить на 4; аналогично выражение 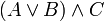
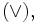
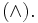
Круглые скобки в математике используются также для выделения аргументов функции: 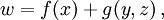
(здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение:
При обозначении диапазона чисел круглые скобки обозначают, что числа, которые находятся по краям множества не включаются в это множество. То есть запись А = (1;3) означает, что в множество включены числа, которые 1(открытый) интервал.
В химических формулах круглые скобки применяются для выделения повторяющихся функциональных групп, например, (NH4)2CO4, Fe2(SO4)3, (C2H5)2O. Также скобки используются в названиях неорганических соединений для обозначения степени окисления элемента, например, хлорид железа(II), гексацианоферрат(III) калия.
Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках.
Во многих языках программирования используются круглые скобки для выделения конструкций. Например, в языках Паскаль и Си в скобках указываются параметры вызова процедур и функций, а в Лиспе — для описания списка.
Квадратные скобки
В лингвистике употребительны для обозначения транскрипции в фонетике или границ составляющих в синтаксисе.
Квадратными скобками в цитатах задают авторский текст, который проясняет контекст цитаты. Например, «Их [заложников] было около 100 человек».
Квадратными скобками в математике могут обозначаться:
В вики-разметке двойные квадратные скобки используются для внутренних ссылок, перенаправлений, категорий и интервики, одинарные — для внешних.
В программировании чаще всего применяются для указания индекса элемента массива.
Часто квадратные скобки используются для обозначения необязательности, например, параметров командной строки (см. подробнее в статье Форма Бэкуса — Наура).
Фигурные скобки
Фигурными скобками в одних математических текстах обозначается операция взятия дробной части, в других — они применяются для обозначения приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок). Фигурные скобки применяют для обозначения множеств. Одинарная фигурная скобка объединяет системы уравнений или неравенств. В математике и классической механике фигурными скобками обозначается оператор специального вида, называемый скобками Пуассона: 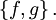
В вики-разметке двойные фигурные скобки применяются для шаблонов.
В программировании фигурные скобки являются или операторными (Си, C++, Perl и комментарием (Паскаль), могут также служить для образования списка (в Сетл).
Угловые скобки
В математике угловыми скобками обозначают кортеж, реже — скалярное произведение в предгильбертовом пространстве, например:
В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как 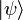
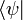
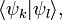
Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например, 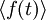
В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте — 
Типографика
В типографике же угловые скобки 
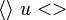
В ТеХе для записи угловых скобок используются команды «\langle» и «\rangle».
ASCII-тексты
В некоторых языках разметки, напр., HTML, XML угловыми скобками выделяют теги.
В вики-разметке также можно использовать HTML-разметку, например комментарии — « », которые видны только при редактировании статьи.
В программировании угловые скобки используются редко, чтобы не создавать путаницы между ними и знаками отношений (« »). Например в Си угловые скобки используются в директиве препроцессора #include вместо кавычек, чтобы показать что включаемый заголовочный файл необходимо искать в одном из стандартных каталогов для заголовочных файлов, например в следующем примере:
файл stdio.h находится в стандартном каталоге, а myheader.h — в текущем каталоге (каталоге исходника программы).
В некоторых текстах, сдвоенные парные « » используются для записи кавычек-ёлочек, например — >.
Косые скобки
Появились на пишущих машинках для экономии клавиш.
В программировании на языке Си косые скобки вместе с дополнительным знаком «*» обозначают начало и конец комментария:
Прямые скобки
Используются в математике для обозначения модуля числа или вектора, определителя матрицы:
Двойные прямые скобки
Используются в математике для обозначения нормы элемента линейного пространства: ||x||; иногда — для матриц:
Скобки
Сюда перенаправляются запросы 🙂 и некоторые другие, начинающиеся с двоеточия. О них см. статью смайлик.
| ( ) | ||
| Название символа | Ско́бки — па́рные знаки, используемые в различных областях. Обычно первая в паре скобка называется открывающей, а вторая — закрывающей. Почти всегда (за исключением некоторых математических обозначений) открывающая и закрывающая скобки соответствуют друг другу (квадратная — квадратной и т. д.). Используются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||. В математике, физике, химии и др. используются при написании формул. Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂. В системе вёрстки TEΧ есть возможность автоматически подстраивать размер скобок под вложенный в него текст: это делается с помощью команд \left и \right. Следует заметить, что во избежание синтаксических ошибок эти две команды всегда должны соответствовать друг другу, однако виды скобок в них — не обязательно. Это делает возможным конструкцию вида «\left\< a \\ a \right.» для записи систем уравнений. СодержаниеКруглые (операторные) скобкиИспользуются в математике для задания приоритета математических и логических операций. Например, (2+3)·4 означает, что надо сначала сложить 2 и 3, а затем сумму умножить на 4; аналогично выражение Круглые скобки в математике используются также для выделения аргументов функции: (здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение: Круглые скобки в математике используются также для указания бесконечно повторяющегося периода позиционного представления рационального числа, например При обозначении диапазона чисел круглые скобки обозначают, что числа, которые находятся по краям множества не включаются в это множество. То есть запись А = (1;3) означает, что в множество включены числа, которые 1(открытый) интервал. В химических формулах круглые скобки применяются для выделения повторяющихся функциональных групп, например, (NH4)2CO4, Fe2(SO4)3, (C2H5)2O. Также скобки используются в названиях неорганических соединений для обозначения степени окисления элемента, например, хлорид железа(II), гексацианоферрат(III) калия. Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках. В русском языке употребляются для выделения пояснительного слова или вставного предложения. Например: Орловская деревня (мы говорим о восточной части Орловской губернии) обыкновенно расположена среди распаханных полей, близ оврага, кое-как превращённого в грязный пруд (И.Тургенев). Во многих языках программирования используются круглые скобки для выделения конструкций. Например, в языках Паскаль и Си в скобках указываются параметры вызова процедур и функций, а в Лиспе — для описания списка. Квадратные скобкиВ лингвистике употребительны для обозначения транскрипции в фонетике или границ составляющих в синтаксисе. Квадратными скобками в цитатах задают авторский текст, который проясняет контекст цитаты. Например, «Их [заложников] было около 100 человек». Квадратными скобками в математике могут обозначаться: В математике помимо обычных квадратных скобок используются также их модификации «пол» В вики-разметке двойные квадратные скобки используются для внутренних ссылок, перенаправлений, категорий и интервики, одинарные — для внешних. В программировании чаще всего применяются для указания индекса элемента массива, в языке Perl также формируют ссылку на безымянный массив; в BASIC и некоторых других достаточно старых языках не используются. Часто квадратные скобки используются для обозначения необязательности, например, параметров командной строки (см. подробнее в статье Форма Бэкуса — Наура). Фигурные скобкиФигурными скобками в одних математических текстах обозначается операция взятия дробной части, в других — они применяются для обозначения приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок). Фигурные скобки применяют для обозначения множеств. Одинарная фигурная скобка объединяет системы уравнений или неравенств. В математике и классической механике фигурными скобками обозначается оператор специального вида, называемый скобками Пуассона: В вики-разметке двойные фигурные скобки <<…>> применяются для шаблонов и встроенных функций и переменных, одинарные в определённых случаях формируют таблицы. В программировании фигурные скобки являются или операторными (Си, C++, Java, Perl и PHP), или комментарием (Паскаль), могут также служить для образования списка (в Mathematica), анонимного хеш-массива (в Perl, в иных позициях для доступа к элементу хеша) или множества (Сетл). Угловые скобкиВ математике угловыми скобками обозначают кортеж, реже — скалярное произведение в предгильбертовом пространстве, например: В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например, В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте — ТипографикаВ типографике же угловые скобки В TEX для записи угловых скобок используются команды «\langle» и «\rangle». ASCII-текстыВ некоторых языках разметки, напр., HTML, XML угловыми скобками выделяют теги. В вики-разметке также можно использовать HTML-разметку, например комментарии — « », которые видны только при редактировании статьи. В программировании угловые скобки используются редко, чтобы не создавать путаницы между ними и знаками отношений (« »). Например в Си угловые скобки используются в директиве препроцессора #include вместо кавычек, чтобы показать, что включаемый заголовочный файл необходимо искать в одном из стандартных каталогов для заголовочных файлов, например в следующем примере: файл stdio.h находится в стандартном каталоге, а myheader.h — в текущем каталоге (каталоге хранения исходного текста программы). Кроме того, угловые скобки применяются в языках программирования C++, Java и C# при использовании средств обобщённого программирования: шаблонов и дженериков. В некоторых текстах, сдвоенные парные « » используются для записи кавычек-ёлочек, например — >. Косые скобкиПоявились на пишущих машинках для экономии клавиш. В программировании на языке Си косые скобки вместе с дополнительным знаком «*» обозначают начало и конец комментария: Прямые скобкиИспользуются в математике для обозначения модуля числа или вектора, определителя матрицы: Двойные прямые скобкиИспользуются в математике для обозначения нормы элемента линейного пространства: ||x||; иногда — для матриц: ИсторияКруглые скобки появились в 1556 году у Тартальи (для подкоренного выражения) и позднее у Жирара. Одновременно Бомбелли использовал в качестве начальной скобки уголок в виде буквы L, а в качестве конечной — его же в перевёрнутом виде (1550); такая запись стала прародителем квадратных скобок. Фигурные скобки предложил Виет (1593). Всё же большинство математиков тогда предпочитали вместо скобок надчёркивать выделяемое выражение. В общее употребление скобки ввёл Лейбниц. См. такжеЛитератураПолезноеСмотреть что такое "Скобки" в других словарях:СКОБКИ — парный знак препинания для выделения отдельных слов или частей предложения, содержащих пояснения к основному тексту. В математике употребляются для обозначения порядка выполнения математических действий. Бывают круглые ( ), квадратные СКОБЛИКОВА… … Большой Энциклопедический словарь скобки — (Square brackets, Parantheses, Angle brackets, Braces) Парные знаки препинания. Бывают квадратные, круглые, угловые (ломаные), фигурные (парантезы). Применяются в формульном наборе и для выделений в тексте … Шрифтовая терминология скобки — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN parentheses … Справочник технического переводчика скобки — парный знак препинания для выделения отдельных слов или частей предложения, содержащих пояснения к основному тексту. В математике употребляются для обозначения порядка выполнения математических действий. Различают скобки круглые ( ),… … Энциклопедический словарь «СКОБКИ» — En.: Parentheses 1. Гипноз позволяет изолировать отдельные психологические функции, «их как бы удается взять в скобки». Другими словами, можно добиться временного «зависания» определенной психической активности в пользу другого ее вида. Пациенту… … Новый гипноз: глоссарий, принципы и метод. Введение в эриксоновскую гипнотерапию Скобки — 1) парный знак препинания, состоящий из двух вертикальных черт: круглых О, квадратных, или прямых, [ ], фигурных, или парантезов, < >. Употребляется для выделения слов, частей предложения или предложений, содержащих дополнительные… … Большая советская энциклопедия скобки — знак препинания. Взятие фрагмента предложения в скобки означает выделение его в качестве дополнительной информации (вставной конструкции): «И каждый вечер, в час назначенный / (Иль это только снится мне?) / Девичий стан, шелками схваченный, / В… … Литературная энциклопедия Скобки — мн. Письменные или печатные знаки (обычно парные), служащие для обособления какой либо части текста, а в математике для обозначения порядка выполнения действий. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой скобки — скобки, скобок, скобкам, скобки, скобками, скобках (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов Для чего нужны скобки в математике?2-й классНа уроке ознакомления с новым материалом дети должны не просто получить готовые знания, а вывести их самостоятельно, выполняя определенные действия. И чем больше таких практических действий будет совершено, тем лучше ученики усвоят новое правило.Тема. "Выражение со скобкой". Цели. Закреплять вычислительные навыки в пределах 20; познакомить с постановкой скобок в примерах в несколько действий, их ролью, с порядком выполнения действий в таких примерах; показать новую запись решения задачи путем составления выражения; развивать наблюдательность, логическое мышление. Оборудование. Карточки с примерами в несколько действий. I. Организационный моментII. Устный счетУчитель. Первый вариант собирает верхнюю дорожку (от 8 до до знака вопроса), а второй вариант – нижнюю. Победит тот, кто раньше других определит число, спрятавшееся под вопросом. Дети выполняют вычисления. – Поздравьте победителя! Дети. В числе 21 – два десятка, одна единица. Оно нечетное, двузначное. В его записи использованы две разные цифры. У. Какие 2 двузначных числа надо сложить, чтобы получить 21? Выслушиваются ответы детей. III. Сообщение темы урокаУ. Чтобы узнать тему нашего урока, вам надо расшифровать запись на доске. Дети производят вычисления, пользуются шифром и читают тему урока. – Что у вас получилось? Д. Выражения со скобками. У. На уроке мы постараемся ответить на вопросы: Что такое "скобка"? Какую роль играют скобки в выражениях? IV. ЧистописаниеУ. На минутке чистописания мы потренируемся правильно записывать разные виды математических скобок. Учитель показывает правильную запись скобок на доске, дети изображают их в тетрадях. V. Знакомство с новым материаломУ. Сравните записи на доске. – Чем похожи и чем отличаются выражения? – Как их прочитать? Как вычислять? Д. Если скобок нет, вычисляем, начиная слева направо. У. Рассмотрите равенство. – Чем похожа левая часть равенства на правую? Чем отличается? Д. Слагаемые те же, но введены скобки. Д. Слагаемые те же, в левой части скобки объединяют первые два слагаемых, а в правой – два последних. У. Изменится ли порядок действий? Д. Да, наличие скобок указывает на порядок действий. У. В каком порядке нужно выполнять действия в левом выражении? А в правом? – Как можно объяснить числа в сумме? Д. Можно складывать любые два соседних слагаемых, а затем прибавлять к ним третье слагаемое. У. Как бы вы могли найти результат в следующем выражении? Дети выходят к доске и записывают варианты решений.
У. А с разностью посложнее!
– Не попадитесь в ловушку! Можно ли в выражениях, где есть разность, ставить скобки так же свободно, как с суммами? Д. Нужно обращать внимание на то, чтобы можно было выполнить действие вычитания, то есть уменьшаемое должно быть больше вычитаемого. У. Какое действие главнее: сложение или вычитание? Д. Оба они равноправны. У. Расставьте порядок действий.
У. Что нужно помнить при решении выражений со скобками? Д. Сначала выполняют действия в скобках, а потом за скобками. – Расставьте порядок действий. Работа выполняется коллективно с комментированием. – А теперь запишите выражения в тетрадь и самостоятельно укажите порядок действий. Дети выполняют задание. Осуществляется проверка. – Зависит ли результат выражения от порядка действий? Д. Если не знать порядка выполнения действий в примерах со скобками, можно решить примеры неправильно. У. А теперь выполним задание по рядам. Вы получаете карточки с математическими выражениями. В них надо указать порядок действий. Так как вычисления в данной работе производить не надо, вместо чисел в выражениях записаны нули. Каждый из вас работает с одним примером, затем передает карточку сидящему сзади. Учитель раздает карточки. После выполнения работы дети, сидящие в разных рядах, меняются карточками и проверяют работу своих соседей. Ошибки разбираются у доски. 0 – 0 + 0 | |
|---|---|---|
VI. Физкультминутка
VII. Закрепление нового материала
У. Предлагаю вам ответить на вопросы теста.
1. В выражении 8 – 2 + 1 действия выполняются:
а) по порядку справа налево;
б) по порядку слева направо;
в) в любом порядке.
2. Отметьте, где правильно расставлен порядок выполнения действий:
– А теперь мы будем учиться составлять и записывать математические выражения.
Один ученик работает у доски, пользуясь помощью учителя, остальные – в тетрадях.
К числу 10 прибавить разность чисел 17 и 9.
Из 12 вычесть сумму чисел 3 и 6.
Разность чисел 12 и 10 увеличить на 5.
К сумме чисел 8 и 3 прибавить разность чисел 14 и 6.
10 + (17 – 9)
(12 – 10) + 5
12 – (3 + 6)
(8 + 3) + (14 – 6)
У. А еще скобки встречаются и в таких выражениях.
х + (
–
) = 5
( 

с – ( 


– Как называются такие выражения?
У. С решением уравнений со скобками вы будете знакомиться позднее.
VIII. Решение задач
У. Прочитайте задачу. Сделайте краткую запись и решите ее.
Иван Царевич и его братья выпускали стрелы. 3 стрелы упали на царский двор, 4 – на боярский, а 8 стрел улетели в неизвестном направлении. Сколько всего стрел выпустили Иван-царевич и его братья?
Два ученика работают на закрытых частях доски.
 |
Решение задачи проверяется.
– А хотите узнать новый способ записи решения задачи? Вы умеете решать задачи по действиям. Сегодня я познакомлю вас с решением задачи путем составления выражения. Поможете мне?
Составьте условие задачи по ее краткой записи.
 |
– Прочитайте только условие задачи! Какой вопрос можно задать?
Д. Сколько-то книг стояло на первой полке, сколько-то – на второй. Надо узнать, сколько книг на двух полках.
У. Чтобы найти, сколько всего книг на двух полках, что нужно знать?
Д. Сколько книг на первой и сколько на второй полках.
У. Какое действие для этого нужно выполнить?
У. Ставим посередине строчки знак "+". Опускаем лист вниз, открывая данные о первой полке.
– Сколько книг на первой полке, нам известно?
У. Пишем число "7" слева от знака "+".
Опускаем лист ниже, открываем данные о второй полке.
– Сколько книг на второй полке, мы знаем?
У. Справа от знака "+" ставим скобки.
– Подумаем, как же найти количество книг на второй полке, если известно, что на этой полке на 4 книги меньше?
У. Это выражение и записываем в скобках.
– Вот мы и записали решение задачи в виде одного выражения. Теперь нужно сосчитать, сколько получится книг.
IХ. Итог урока
У. Что нового вы узнали на уроке? Для чего применяются скобки в математике?
Х. Домашнее задание
1. Составить задачу и решить ее с помощью выражения.
2. Составить 5 математических выражений со скобками из 4–5 чисел для соседа, записать их на карточке.

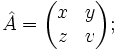
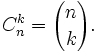
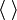
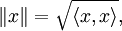
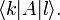
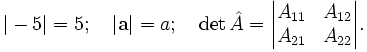
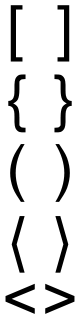
 означает, что сначала выполняется логическое сложение
означает, что сначала выполняется логическое сложение  а затем — логическое умножение
а затем — логическое умножение  Наряду с квадратными скобками используются также для записи компонент векторов:
Наряду с квадратными скобками используются также для записи компонент векторов:


 для обозначения открытого сегмента и в некоторых других контекстах. Иногда круглыми скобками обозначается скалярное произведение векторов:
для обозначения открытого сегмента и в некоторых других контекстах. Иногда круглыми скобками обозначается скалярное произведение векторов:


 и «потолок»
и «потолок»  для обозначения ближайшего целого, не превосходящего
для обозначения ближайшего целого, не превосходящего  , и ближайшего целого, не меньшего
, и ближайшего целого, не меньшего  Как уже было сказано выше, иногда фигурными скобками обозначают антикоммутатор.
Как уже было сказано выше, иногда фигурными скобками обозначают антикоммутатор.
 (кет-вектор) и
(кет-вектор) и  (бра-вектор), их скалярное произведение как
(бра-вектор), их скалярное произведение как  матричный элемент оператора А в определённом базисе как
матричный элемент оператора А в определённом базисе как 
 — среднее значение по времени от величины f.
— среднее значение по времени от величины f. .
. являются самостоятельными символами. От « » их можно отличить по бо́льшему углу между сторонами —
являются самостоятельными символами. От « » их можно отличить по бо́льшему углу между сторонами —  и
и  " border="0" />.
" border="0" />.

.svg.png)



