Что означают цифры после слова в русском языке
Как сделать разбор под цифрой 4 по русскому языку?
Все-таки как полезно отвечать на различные вопросы сайта Большой вопрос, вспоминаешь все, что давно забыл, мозгу не даешь совсем заснуть, да и грамотности своей под влиянием интернет-потока безграмотности не даешь совсем уж упасть ниже плинтуса.
Если мы видим цифру четыре после предложения, то мы должны сделать разбор синтаксический. Вспоминаем, что это такое. Буду частично давать свой текст в формате цитаты, чтобы уникальность не была слишком низкой, потому что многие вещи своими словами не напишешь.
Рассмотрим все то, что я написала выше в своем ответе на примере вот такого предложения:
Ну вот, кажется, разобрались, но запомнить это, конечно, довольно сложно, придется все-таки воспользоваться учебником или интернетом, если когда-нибудь придется повторить этот подвиг.
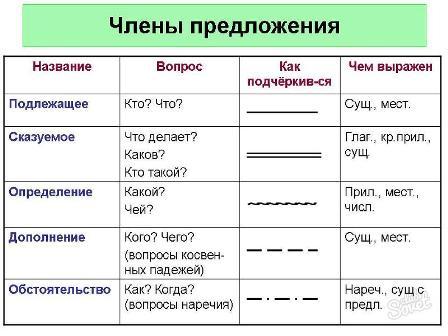
В конце предложения нередко пишется цифра 4. Это означает, что необходимо сделать синтаксический разбор предложения. Выделить подлежащее и сказуемое. В некоторых случаях пишется часть речи над словом.
Синтаксический разбор предложения выполняется по следующему плану:
Далее, в зависимости от предложения, сложного или простого, следует придерживаться данного плана:
Но в любом случае, вам необходимо будет подчеркнуть все члены данного предложения и указать, какими частями речи они являются. Чтобы правильно это определить, следует задавать вопросы к второстепенным членам предложения.
После всего иногда составляется схема предложения.
Разбор под цифрой 4 в учебниках русского языка подразумевает синтаксический разбор предложения, который выполняется по следующему плану.
Над каждым словом надо написать часть речи. В скобках указать какое это предложение и нарисовать схему.
что такое разбор под цифрой 4
цифра 4 это какой разбор по русскому языку
Цифра 4 в конце предложения указывает на то, что необходимо сделать синтаксический разбор этого предложения.
Привожу план и примеры синтаксического разбора разных видов предложения.
Разбор под цифрой четыре означает синтаксический разбор.
Далее найдем главные члены предложения и подчеркнем их.
После этого нам нужно найти второстепенные члены предложения и подчеркнуть их, после этого над каждым словом предложения укажем часть речи.
И не забудем составить схему предложения.
Если вы увидели то, что в конце предложения, находится цифра «4», то это означает то, что вам нужно произвести синтаксический разбор данного предложения.
Ну а этот разбор по сути предполагает то, что вы должны будете выявить в предложении подлежащее и сказуемое и подчеркнуть их, подлежащее одной чертой, а сказуемое двумя. Затем так же выявляете второстепенные члены предложения, которыми могут являться: определение, обстоятельство или дополнение. Чаще всего в данном разборе, требуется над каждым словом, надписать кратко, к какой части речи оно относится.
В завершении, вы анализируете и описываете все предложение в целом и дополнительно указываете, чем данное предложение осложнено.
К примеру предложение может быть: вопросительным или же повествовательным.
распространенное или нет ( если в предложении кроме подлежащего и сказуемого, есть и другие члены, то оно распространенное)
осложнено ли оно чем то или нет. ( может быть осложнено например однородными сказуемыми или определениями)
Под данной цифрой принято считать синтаксический разбор. С помощью этого разбора можно понять характеристику предложения, к примеру предложение может оказаться вопросительным.
Так же важно понять относится предложение к простому или сложному. От этого зависит, как делать разбор дальше.
В целом синтаксический разбор не так уж и прост. Посмотрите ниже памятку, там указаны все пункты такого разбора. Делайте разбор по порядку по пунктам.
Разбор предложения под цифрой 4 означает его синтаксический разбор.
Примерный план синтаксического разбора:
Также синтаксический разбор подразумевает определение частей речи для каждого слова, и эти части речи нужно написать сверху над каждым словом.
Владимир Клавдиевич Арсеньев — знаменитый русский исследователь Дальнего Востока, ________________ ____
________ _ _ _ _ _ _ _ _ _ _
____
Повествовательное, невосклицательное, простое, распространённое, с однородными сказуемыми.
Числа в тексте: что можно, что нельзя, что нежелательно
Приветствую вас! Это Юлия. Сегодня речь пойдет о числах в тексте. Они сигнализируют: тут есть точная информация, все конкретно и по делу. Чтобы вас сразу правильно поняли и не “спотыкались” при прочтении, нужно выбрать: писать число цифрами или словами.
Когда ставить сокращение рядом? А пробел? Я собрала все, что может быть полезным на эту тему, чтобы вы с чистой совестью отправили статью в закладки и использовали как памятку. Итак.
Цифра или слово: общее правило
Для упрощения восприятия текста двузначные и многозначные числа пишутся цифрами.
А числа от одного до девяти пишем словом, если они не в именительном падеже. Тогда мы не проделываем в уме путь “прочитал цифру – не согласовал со словом – перечитал, чтобы поставить в правильный падеж”.
А в именительном падеже можно и так, и так:
В начале предложения, пункта списка пишется слово.
О начале предложения читателю говорит заглавная буква. Одной точки мало, это сбивает.
То же и с пунктами списка, об оформлении которых мы говорили уже довольно давно. Если список нумерованный или каждый пункт начинается заглавной буквой и оканчивается точкой, то начинать подпункты нужно словом.
Начинать предложение цифрой можно в заголовках и подзаголовках. Например, как в нашей статье: 15 слов, во множественном числе которых мы то и дело путаемся.
Если в тексте встречаются подряд два числа, одно из них нужно заменить словом или перестроить предложение.
Подробнее о написании однозначных цифр
От общего правила переходим к уточнениям.
Однозначное число стоит рядом с многозначными при перечислении? Пишите цифрой.
Однозначное число обозначает физическую величину, денежную единицу? Пишите цифрой.
Но! Если физическая величина обозначается буквами, а не сокращением, то оставляем словесную форму: два джоуля.
Подробнее о написании многозначных цифр
Числа от 10 почти всегда предпочтительно писать цифрами. Цифровая форма лучше воспринимается и запоминается читателю, она заметнее в тексте.
Когда числа нужно разбивать пробелами
Технические правила набора рекомендуют разбивать пробелами цифры, начиная с 5-значных. Допустимо разбивать и 4-значные математические значения.
Отбиваем пробелом с конца по три цифры. И читателю уже не нужно проделывать это мысленно. Это правило действует только для цифровых величин.
Не разбиваются пробелами: годы, номера после знака №, номера документов, номера марок машин и т.п.
| Рекомендуется ✅ |
| Родился в 1974 году. |
| В соответствии с ГОСТ 210586 |
| Дело № 6666 |
Точка в пробелах между цифрами не ставится:
Знаки сокращения после цифр
Для обозначения крупных круглых чисел (от 1 000) предпочтительно использовать знаки сокращения.
Слова, обозначающие сокращения, отбиваются от цифр пробелами.
Обозначения физических величин тоже отбиваются от цифр пробелами.
В перечислениях символы ставятся один раз:
№, § – в начале перечисления: № 3, 5, 10, 23.
%, ° (без Цельсия) – после перечисления: 10, 20, 80 %.
Не ставятся точки после сокращений:
После остальных сокращений точка ставится (г. (год), мес., мин., руб., тыс. и т. д.).
Дробные числа: какой ставить падеж
Дробное число управляет существительным при нем. Существительное ставят в родительный падеж единственного числа (вопрос: кого? чего?). Например:
Обозначение числовых интервалов
Для обозначения интервала значений можно ставить:
Не рекомендуется ставить тире как знак интервала значения, когда одно значение положительное, а второе – отрицательное, или оба отрицательные.
При обозначении крупных круглых чисел в цифровой форме нули не сокращаются:
При словесно-цифровой форме рекомендуется сокращения тыс., млн, млрд не повторять.
Надеюсь, статья была полезной. Если что-то осталось незатронутым – давайте разбирать в комментариях!
6. Числа и знаки
6.1.2. Однозначные числа
Могут быть написаны прописью или в цифровой форме.
Словесная форма чисел (прописью). Рекомендуется в следующих случаях:
1. Когда однозначные числа стоят в косвенных падежах не при единицах величин, денежных единицах, поскольку в подобных случаях цифровая форма усложнила бы чтение (поначалу читатель мысленно произносит цифру в им. падеже и лишь при дальнейшем чтении понимает, что падеж должен быть иным, а это ведет к ненужной остановке, замедляет чтение). Напр.:
Лабораторию следует оборудовать четырьмя мойками.
Лабораторию следует оборудовать 4 мойками.
2. Когда стечение нескольких чисел в цифровой форме может затруднить чтение, а вставить между этими числами слово или изменить порядок слов, чтобы развести числа, сложно или нежелательно. Напр.:
. пять 30-местных автобусов.
. 5 30-местных автобусов.
Если вставить слово или изменить порядок слов несложно, то предпочтительнее сделать это, чем менять цифровую форму числа на словесную. Напр.: . 25 новых 30-местных автобусов.
3. Когда количественное числительное начинает собой предложение, поскольку при цифровой форме исчезает, как правило, прописная буква в первом слове предложения, служащая для читателя сигналом о его начале (одна предшествующая точка — слабый сигнал для этого). Напр.:
. при такой планировке. Пять станков размещают..
. при такой планировке. 5 станков размещают.
Во избежание разнобоя в написании количественных числительных, стоящих в начале и середине предложения, желательно по возможности перестроить предложение, начинающееся числом, так, чтобы последнее перешло в середину. Напр.: . при такой планировке. Размещают 5 станков.
Цифровая форма. Рекомендуется в следующих случаях:
1. Когда однозначные целые числа, даже в косвенных падежах, стоят в ряду с дву- и многозначными, поскольку при восприятии ряда чисел читателю, как правило, не требуется мысленно переводить их в словесную форму.
За сериями из 3, 5, 12 упражнений следовали.
За сериями из трех, пяти, двенадцати упражнений следовали.
За сериями из трех, пяти, 12 упражнений следовали.
2. Когда однозначные целые числа образуют сочетание с единицами физ. величин, денежными единицами и т. п. Напр.:
При массе до семи кг (до семи килограммов).
Цена до семи р. (до семи рублей).
6.1.3. Многозначные целые числа
Словесная форма чисел. Эта форма рекомендуется при стечении двух чисел в цифровой форме и в случаях, когда предложение начинается числом. Если словесная форма чисел нежелательна, необходимо перестроить фразу, чтобы развести два числа или чтобы не начинать фразу числом, либо заменить точку точкой с запятой. Напр.:
. 3 200 двадцатитонных грузовиков;
. 3 200 20-тонных грузовиков…
. 3 200 грузовиков грузоподъемностью 20 т…
. более целесообразно. Двести пятьдесят станков размещают.
. более целесообразно. 250 станков.
. более целесообразно; 250 станков размещают.
. более целесообразно. Часть станков (250 из общего числа) размещают.
Цифровая форма чисел. Является для многозначных чисел предпочтительной в подавляющем большинстве случаев, поскольку она лучше, чем словесная форма, воспринимается читателями, более заметна, лучше запоминается.
Разбивка чисел в цифровой форме на группы. Такие числа делят пробелами на группы (по три цифры справа налево). Техн. правила набора дают указание разбивать на группы числа только начиная с 5-значных (см.: Наборные и фотонаборные процессы. М., 1983. П. 2.3.9), а «Основные математические обозначения (СЭВ PC 2625—70)» не делают исключения и для 4-значных чисел. Напр.:
Не разбиваются на группы цифры в числах, обозначающих год, номер (после знака номера), в числах обозначений марок машин и механизмов, нормативных документов (стандарты, техн. условия и т. п.), если в документах, устанавливающих эти обозначения, не предусмотрена иная форма написания. Напр.: В 1999 году; № 89954; ГОСТ 20283. По-иному разбиваются номера телефонов (см. 6.1.6).
Точку в пробелах между цифровыми группами ставить запрещается.
Размер отбивки между цифровыми группами 2 п.
Словесно-цифровая форма чисел. Рекомендуется в следующих случаях:
1. Для обозначения крупных круглых чисел (тысяч, миллионов, миллиардов) в виде сочетания цифр с сокращением тыс., млн, млрд, поскольку читатель быстрее, легче воспримет 20 млрд, 12 млн, чем 20 000 000 000, 12 000 000.
Это правило в изданиях для специалистов распространяется и на сочетания крупных круглых чисел с обозначениями единиц физ. величин, денежных единиц и т. п. Напр.:
В изданиях для массового читателя рекомендуется в подобных случаях отказываться не от словесно-цифровой формы чисел, а от сокращенных обозначений единиц величин — заменять их полными наименованиями. Напр.: 20 млн километров, 500 тыс. вольт.
2. В устоявшихся названиях широко известных судебных процессов, чтобы не нарушать традиционное, привычное написание. Напр.: Процесс 193-х; Процесс 50-ти.
6.1.4. Дробные числа
Форма набора простых дробей. Простые дроби принято набирать цифрами на верхнюю и нижнюю линии шрифта: 3 /4. Но для набора именно таким образом наборщик должен получить письменное указание. Поэтому в оригинале простые дроби, написанные в одну линию через косую черту, следует пометить верхней или нижней дугой, повторить ее на боковом поле и рядом написать в кружке: дробь. Напр.:
В выборах приняла участие всего

Простую дробь набирают без отбивки от целого числа. Напр.: 5 1 /2.
Форма набора десятичных дробей. Дробная часть десятичных дробей, как и целые числа, делится пробелами на группы по 3 знака в каждой, но в обратном направлении по сравнению с целыми числами, т. е. слева направо. Напр.:
25,128 137; 20 158,675 8
Падеж существительных при дробных числах. Дробное число управляет существительным при нем, и поэтому последнее ставят в род. падеже ед. ч. Напр.: 1 /3 метра; 0,75 литра; 0,5 тысячи; 10 5 /6 миллиона.
Употребление слов часть, доля при дробных числах. Как правило, следует считать словесным излишеством употребление слов часть, доля после простых дробных чисел. Напр.:
1 /2 часть квадрата; 1 /5 доля площади
6.1.5. Интервал значений
Обозначение интервала значений. Для обозначения интервала значений ставят: а) многоточие; б) тире; в) знак ÷; г) предлог от перед первым числом и до — перед вторым. Напр.: Длиной 5. 10 метров; Длиной 5—10 метров; Длиной 5÷10 метров; Длиной от 5 до 10 метров.
Предпочтительным для изданий техн. и науч. (в области точных и естественных наук) лит. является стандартный знак многоточие (. ) между числами в цифровой форме.
В техн. лит. по традиции допустимо применять знак ÷ между числами в цифровой форме.
Тире и предлоги употребляются в изданиях гуманитарной и публицистической лит.
Употребление тире. Тире в качестве знака интервала значений рекомендуется ставить:
1. При словесной форме чисел (прописью) в изданиях худож. лит., а также близких к ней. Напр.: . длиной пять — десять метров. При этом, как и обычно между словами, тире, по техн. правилам набора, должно быть отбито от слов на 2 п., что и должно быть обозначено в оригинале.
2. В тексте изданий общественно-полит., гуманитарной и подобной лит. Напр.: План выполнялся на 110—115 процентов; 30—35 тыс. юношей и девушек. При этом, как и обычно, между числами в цифровой форме, тире, по техн. правилам набора, не должно отбиваться от цифр.
Не рекомендуется применять тире в качестве знака интервала значений, когда одно из значений величины положительное, а другое — отрицательное или когда оба значения отрицательные. Напр.:
Употребление дефиса. Когда два числа в словесной форме (прописью) означают не «от такого-то до такого-то числа», а «то ли то, то ли другое число», то между числительными ставят дефис. Напр.: У дома стояло машин пять-шестъ. В цифровой форме сохраняется тире: машин 5—6.
Крупные числа в интервале значений. При цифровой форме чисел необходимо сохранять нули в числе нижнего предела, чтобы читатель не мог принять его за меньшее значение. Напр.:
Высота 15 000—20 000 м
(если 1-е число 15 000)
При словесно-цифровой форме чисел допустимо опускать в числе нижнего предела обозначение тыс., млн., млрд., поскольку читатель воспринимает такие обозначения как составную часть единицы величины. Напр.:
Высота 20—30 тыс. метров.
Высота 20 тыс. — 30 тыс. метров.
Расположение чисел в интервале значений. Как правило, от меньшего к большему, от нижнего предела к верхнему. Исключение составляют взаимосвязанные относительные числа (во второй паре большее число может идти первым). Напр.: Это составляет 60—80 % всей массы груза. Остальные 40—20 %.
6.1.6. Номера телефонов
Их принято писать без знака номера, отделяя дефисом или пробелом по две цифры справа налево, напр.: 2-99-85-90; 2-95; 2 99 85 90.
Если в первой группе цифр телефонного номера одна цифра, ее допустимо объединять в одну группу со следующими двумя цифрами. Напр.: 299-85-90, 299 85 90, 295.
6.1.7. Номера домов
Их принято писать без знака номера. Напр.: Тверская, 13. Особенностью отличается написание двойных и литерных номеров.
Двойные номера. Их принято писать через косую черту: ул. Пушкина, 15/18.
Литерные номера. Литеру принято писать слитно с последней цифрой номера: Пушкинский пер., д. 7а.
6.1.8. Сочетания чисел с обозначениями единиц физических величин
500 т; 485 °С; 20 %; 15°; 45′; 15″
500т; 485°С; 20%; 15 °; 45 ‘; 15 «
В сочетании десятичных дробей с обозначениями единиц физ. величин эти обозначения следует помещать после всех цифр. Напр.:
586,5 кг; 30,2°; 36,6 °С; 10°20,5′
586 кг,5; 30°,2; 36°,6; 10°20′,5
Числовое значение с допуском или с предельными отклонениями при сочетании с обозначением единицы физ. величины требуется заключить в скобки либо обозначение единицы поставить и после числового значения, и после допуска или предельного отклонения. Напр.:
(10 ± 0,1) мм; 10 мм ± 0,1 мм
При интервале и перечне числовых значений одной физ. величины обозначение единицы физ. величины ставят только после завершающей цифры. Напр.:
От 50 до 100 м; 50-100 м;
Доски длиной 5, 10, 15 м
Доски длиной 5 м, 10 м, 15 м
6.1.9. Предельные отклонения линейных размеров
Указываются в такой форме:
6.1.10. Правила записи чисел в десятичной системе счисления
СТ СЭВ 543—77, который их установил, распространяет их только на нормативно-техн., конструкторскую и технологическую документацию. Но они вполне применимы и для многих изданий литературы по точным, естественным наукам и технике.
Обозначение точности числа. Для такого обозначения либо после числа ставят слово точно в круглых скобках; напр.: 3 600 000 Дж (точно), либо последнюю значащую цифру выделяют шрифтом полужирного начертания; напр.: 3,6 МДж.
Запись допускаемых отклонений. У последней значащей цифры и числа, и отклонения должен быть одинаковый разряд. Напр.:
17 ± 0,2; 17,00 ± 0,2; 12,13 ± 0,2;
12,1 ± 0,17; 46,405 ± 0,15;
Запись интервалов между числовыми значениями. Форма записи:
6.1.11. Правила округления чисел в десятичной системе счисления
Установлены СТ СЭВ 543—77.
Первая из отбрасываемых цифр (считая слева направо) меньше 5. Последняя сохраняемая цифра не меняется. Напр.:
12,23 

12,23 
565,46 
565,46 
12 456 
12 456 
Первая из отбрасываемых цифр (считая слева направо) равна или больше 5. Последняя сохраняемая цифра увеличивается на единицу. Напр.:
0,145 
0,152 
565,46 

0,156 
0,162 
565,46 

Первая из отбрасываемых цифр (считая слева направо) равна 5, но получена в результате предшествующего округления. В этом случае округление зависит от способа округления первой из отбрасываемых цифр:
а) при ее округлении в большую сторону (напр., 0,15 получено при округлении 0,148) последняя сохраняемая цифра не меняется: 0,15 
б) при ее округлении в меньшую сторону (напр., 0,25 получено при округлении 0,252) последняя сохраняемая цифра увеличивается на единицу: 0,25 
Издания художественной и близких ей литератур
6.1.12. Словесная форма (прописью)
Эта форма, как правило, является рекомендуемой, поскольку цифры придают тексту деловой вид. Напр.: . Мне известен человек, который при росте примерно сто шестьдесят пять сантиметров носит обувь сорок пятого размера (В. Липатов).
6.1.13. Цифровая форма
Как исключение цифровая форма предпочтительна в следующих случаях:
1. Когда требуется имитировать документы, письма, вывески, поскольку пропись в них маловероятна и будет нарушать их «подлинность». Напр.: Будьте сегодня в 7 часов в беседке у ручья (записка Дубровского).
2. Когда в авт. тексте (не в прямой речи) приводятся номера домов, учреждений и т. п. и необходимо передать их в том виде, в каком они предстают на бланке, вывеске и т. п. Напр.: Здесь в столовой № 68, где раньше помещалось. кафе «Флорида». (Ильф И., Петров Е. Золотой теленок).
3. Когда в прямой речи встречается сложный номер и стремятся упростить его чтение. Напр.: «ЛД 46-71», — прочитал Иван номер (Р. Погодин).
4. Когда стремятся подчеркнуть (иногда иронически) особую точность чисел. Напр.: Солнце встало над холмистой пустыней в 5 часов 02 минуты 46 секунд (Ильф И., Петров Е. Золотой теленок).
6.2. Порядковые числительные
Издания деловой и научной литератур
6.2.1. Порядковые числительные в виде арабских цифр с наращением падежного окончания
Это преимущественная форма порядковых числительных в изданиях деловой и науч. лит. Исключение составляют только те объекты, которые принято обозначать римскими цифрами (см. 6.2.5), простые числительные типа первый раз, второй раз, а также те, что обозначают номера элементов издания и следуют за названием этих элементов, и даты (см.6.2.4).
6.2.2. Правила наращения падежного окончания
Падежное окончание в порядковых числительных, обозначенных арабскими цифрами, по закрепившейся традиции должно быть:
1. Однобуквенным, если последней букве числительного предшествует гласный звук. Напр.:
5-й (пятый, пятой), 5-я (пятая)
5-е (пятое, пятые), 5-м (пятым, пятом)
5-ый, 5-ой, 5-ая, 5-ое, 5-ые, 5-ым, 5-ом, 5-ых
2. Двухбуквенным, если последней букве числительного предшествует согласный. Напр.:
6.2.3. Наращения падежного окончания при нескольких порядковых числительных подряд
Написание порядковых числительных с наращением падежного окончания различается в этом случае в зависимости от их числа и формы разделения (соединения):
1. Если один за другим следуют два порядковых числительных, разделенных запятой или соединенных союзом, падежное окончание наращивают у каждого из них. Напр.: 1-й, 2-й ряды; 9-е и 10-е классы; 40-е и 50-е годы; в 8-й или 9-й класс.
2. Если один за другим следуют более двух порядковых числительных, разделенных запятой, точкой с запятой или соединенных союзом, падежное окончание наращивают только у последнего числительного. Напр.: Ученики 5, 7, 9-х классов; 8, 11, 15, 18-й секторы; 40, 60, 70-е годы; в 7, 8 или 9-й класс.
3. Если подряд идут два числительных через тире, то падежное окончание наращивают:
а) только у второго, когда оно одинаковое у обоих числительных, напр.: 50—60-е годы; в 20—30-х гг.;
б) у каждого числительного, когда падежные окончания у них разные или когда предшествующие первому числительному слова управляют только им и не связаны со вторым, напр.: в 20-м—30-х секторах; в начале 70-х-80-е годы.
6.2.4. Порядковые числительные в виде арабских цифр без наращения падежного окончания
К таким числительным относятся:
1. Номера томов, глав, страниц, иллюстраций, таблиц, приложений и т. п. элементов изданий, если родовое слово (название элемента: том, глава и т. д.) предшествует номеру. Напр.: в томе 6; главе 5; на с. 85; на рис. 8; в табл. 11; в прил. 6.
Однако если родовое название элемента стоит после числительного, последнее следует писать с наращением падежного окончания. Напр.: в 6-м томе; в 5-й главе; на 83-й странице.
2. Даты (годы и числа месяца), если слово год или название месяца следует за числом. Напр.: В 1997 году; 12 декабря 1997 года. Не: В 1972-м году; 12-го декабря 1997-го года.
Однако если слово год или название месяца опущено или поставлено перед числом, падежное окончание рекомендуется наращивать. Напр.: в мае, числа 20-го; год 1920-й; Грянул 1917-й; Концерт перенесли с 15 мая на 22-е; 20-го же апреля.
6.2.5. Порядковые числительные в виде римских цифр
Традиционно ими обозначают: 1) номера съездов, конференций, конгрессов и т. п. (XX съезд); 2) века (XXI век); 3) номера международных объединений (III Интернационал); 4) номера выборных органов (IV Государственная дума); 5) номера продолжающихся спортивных состязаний (XX Олимпийские игры); 6) номера в имени императора, короля (Петр I, Николай II, Карл V, Людовик XIV); 7) обозначения кварталов года (IV квартал). Могут обозначаться римскими цифрами квадранты, части или разделы книг и т. п.
Издания художественной и близких ей литератур
6.2.6. Преимущественная форма
Как правило, это словесная форма (пропись). Напр.: В двадцатом веке; в сорок пятом году. В репликах действующих лиц драматического произведения словесная форма порядковых числительных является единственной.
6.2.7. Цифровая или словесно-цифровая форма
Допускается в следующих случаях:
1. Когда требуется стилизовать внешний вид записки, письма, надписи. Напр.: . со свежим известковым лозунгом: «Привет 5-й окружной конференции. » (Ильф И., Петров Е. Золотой теленок).
2. Когда требуется назвать номер газеты, журнала, воинской части, а непрямая речь, в которую он включен, содержит элементы делового характера или когда сам номер сложен для воспроизведения прописью. Напр.: . билет 2-го займа с подмоченным углом (А. П. Чехов); Дивизия в составе 9-го мотополка «Вестланд», 10-го мотополка «Германия». (Эм. Казакевич).
3. Когда необходимо назвать год или число месяца в описательной части произведения. Напр.: В конце 1811 года, в эпоху нам достопамятную. (А. С. Пушкин).
Однако цифровая форма в подобных случаях не подходит, если точность датировки не имеет существенного значения, а окружающий текст не носит описательного характера или если год обозначается сокращенно. Напр.: Прошлого года двадцать второго марта вечером со мной случилось. (Ф. М. Достоевский); Революция семнадцатого года. (Ильф И., Петров Е.).
4. Когда в описательной части произведения требуется назвать имя императора, короля с номером в составе имени. Напр.: . Локоны. взбиты были, как парик Людовика XIV(Пушкин А. С. Барышня-крестьянка).
6.3. Числительные в составе сложных существительных и прилагательных
6.3.1. Издания художественной и близких ей литератур
Применяется, как правило, словесная форма (пропись). Напр.: пятидесятилетие; двадцатикилометровый переход.
6.3.2. Издания массовой не художественной литературы
Рекомендуется словесно-цифровая форма (число в цифровой форме и присоединяемое дефисом существительное или прилагательное). Напр.: 150-летие, 20-километровый переход, 25-процентный раствор.
Неверно: 150-тилетие, 20-тикилометровый переход и т. п., т. е. с присоединением ко второй части слова окончания числительного.
6.3.3. Издания деловой и научной литератур
Рекомендуется словесно-цифровая форма, даже когда числа малы. Напр.: 1-, 2- и 3-секционные шкафы; 3- и 4-красочные машины.
В узкоспец. изданиях для высокоподготовленного читателя допустимо прилагательное, присоединяемое к числу, если оно образовано от названия единицы физ. величины, заменять обозначением этой единицы. Напр.: 5-км расстояние; 12-т нагрузка.
6.3.4. Сложные слова из числительного и прилагательного процентный
Предпочтительной в таких изданиях следует считать форму с наращением одно- или двухбуквенного окончания по правилам наращения падежного окончания в порядковых числительных, обозначенных арабскими цифрами (см. 6.2.2). Напр.: 15%-й раствор, 20%-го раствора, 25%-му раствору и т. д. Такая форма экономнее предыдущей и позволяет соблюсти единообразие в наращении падежных окончаний.
В узкоспец. изданиях для высокоподготовленного читателя допустима форма без наращения падежного окончания, если контекст не может вызвать двояких толкований. Напр.:В 5% растворе.
6.4. Знаки в тексте
6.4.1. Замена слов в тексте знаками
Как и сокращения, знаки, которые во многих случаях могут заменить слова, экономят место в издании и время читателя. Наиболее употребительны в тексте знаки номера (№), параграфа (§), процентов (%), градуса (°), минуты (‘), секунды («). Читатель без расшифровки знака, без мысленного перевода его в словесную форму, по одному только графическому образу знака может мгновенно сориентироваться в значении числа. Знаки и пришли на смену словам, когда понадобилось самым быстрым и экономным способом указать читателю, каков характер чисел в цифровой форме: обозначают ли они порядковые номера или род заголовка либо числовое значение определенной величины.
6.4.2. Знаки №, %, §, ° в тексте
Эти знаки в тексте ставят только при числах в цифровой форме: № 5, § 11, 45 %, 30°. При числах прописью их принято заменять словами: номер пять, в параграфе втором, сорок пять процентов, пять градусов.
Знак % заменяют словом и при числе в цифровой форме, если текст публицистический или популярный, рассчитанный на массового читателя: 45 процентов.
Выброска знака № перед числами. Так поступают, когда и без знака № ясно, что число обозначает порядковый номер (напр., перед номерами страниц, столбцов, таблиц, формул, примечаний, приложений, деталей схемы и т. п.). Напр.: на с. 8; стб. 805; в приложении 3; в табл. 5; на рис. 8; в равенстве (5); из формулы (6); Примечание 5; винт 5 на рис. 10.
Знаки №, §, %, ° — при двух и более числах. Исходя из принципа экономии средств эти знаки набирают только перед рядом чисел или после него, без постановки у каждого числа в числовом ряду. Напр.;
№ 5, 6, 7; 8, 9°; 50, 60 и 70 %;
От 50 до 70 %; § 5 и 6
№ 5, № 6, № 7; 8°, 9°, 60 % и 70 %;
От 50 % до 60 %, § 5 и § 6
Если при этом числа представляют собой десятичные дроби, то их, во избежание неверного или затрудненного прочтения, отделяют друг от друга не запятой, а точкой с запятой. Напр.:
Правила набора. Знаки №, % и § отбивают от цифр на полукегельную. Знаки градуса, минуты и секунды от цифр не отбивают. Знак °С отбивают, как и другие обозначения единиц физ. величин, на 2 п.
6.4.3. Знаки более (>), менее ( ↑ Cодержание ↑
6.4.4. Знаки математических действий и соотношений, положительности и отрицательности значения величин
) отбивают от смежных символов и чисел на 2 п., а знаки положительности или отрицательности значения величины набирают слитно с последующим числом.
6.4.5. Знаки ударения и произношения в словах текста
Эти знаки облегчают и упрощают чтение. Так, знак ударения или две точки над буквой е (ё) помогают читателю с первого раза правильно прочесть текст в случаях, когда возможно двойное прочтение. Напр.: по´длиннее и подлинне´е; бо´льшая часть и больша´я часть; Всё деревушки были неказистые и Все деревушки были неказистые; Я видел из окна, что´ происходило на улице и Я видел из окна, что на улице толпились люди (подробнее см. 5.5).