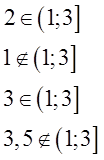Что означают три вертикальные точки в математике
Что такое три точки в математике?
Что означает математический знак три точки?
ellipsis — незаполненность) — самостоятельный типографский знак, разновидность отточия, состоящий из трёх точек идущих подряд, используется для обозначения скрытого смысла, особенностей устной речи (вздох, пауза, задумчивость), недосказанности либо для исключения из текста некоторых слов, например при цитировании.
Что значит вертикальное троеточие в математике?
Встретила в леции для семиклассников такой знак — вертикальное троеточие. По контексту — эта запись означает «доказать, что разность кубов делится на 25».
Что означает точки в математике?
То́чка — одно из фундаментальных понятий математики, абстрактный объект в пространстве, не имеющий никаких измеримых характеристик (нульмерный объект). … В частности, геометрические точки не имеют никакой длины, площади, объёма или какой-либо другой размерной характеристики.
Что такое с в математике?
C — 16-ричное представление числа 12 (а также представление числа 12 в 13-ричной системе счисления или в любой другой системе счисления с основанием, большим числа 12).
Как называется этот математический знак?
Знаки операций, или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: −
Что означают буквы SVT в математике?
S = V×t. В данной формуле S — это путь, V — скорость, а t — время. Эта формула справедлива только для случаев, когда движение было с одной скоростью. Например, грузовик ехал из одного города в другой 3 часа с постоянной скоростью 60 км/ч.
Что означает Три точки в конце предложения?
то же, что многоточие; знак препинания в виде трёх точек, ставящийся в конце предложения или в середине и означающий паузу, незавершённость, задумчивость и т. п.
Что такое ≈?
«≈» — «приблизительно равно». Используется при обозначении двух величин, разницей между которыми в данной задаче можно пренебречь. «≃» — используется для обозначения гомеоморфных пространств в топологии.
Что означает многоточие в математике?
многоточие используется для обозначения произвольного количества неизвестных аргументов в описании функции. Например: int printf(const char * fmt, …); означает, что у функции printf первый аргумент имеет тип const char *, а дальше может быть любое число аргументов с произвольными типами.
Как обозначается точка в геометрии?
В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы. В тексте точку обозначают следующим символом: «(·) A» — точка «А».
Как в геометрии обозначаются точки и прямые?
Точки обозначаются большими латинскими буквами, прямые обозначаются малыми латинскими буквами.
Как обозначается плоскость в геометрии?
Что такое V в задачах?
Расстояние обозначается латинской буквой S. Скорость – это расстояние, пройденное телом за единицу времени. … Скорость обозначается латинской буквой v.
Что такое S в задаче?
S V t Задачи на движение В задачах на движение рассматриваются три взаимосвязанные величины: S — расстояние (пройденный путь), t — время движения и V — — презентация
Что означает символ )))?
Символ — знак, изображение какой-нибудь вещи или животного для обозначения качества предмета. Символ, в психоанализе — образ, наделенный знаковостью и смыслом, имеющий отношение к чему-то другому и являющийся его представителем. «Символ» — советский бытовой компьютер начала 1990-х годов, клон ZX Spectrum.
Что значит три точки в сообщении
Как много несут в себе смысла простые знаки препинания? Без восклицательных и вопросительных знаков текст обеднеет и рассыплется ничего не выражающими фразами. А точки и запятые – естественные барьеры, без которых нельзя придумать ни одного предложения.
Есть еще один знак, заслуживающий внимания – многоточие. Что означает и где оно применяется? Как не переборщить с точками, уместно вставить их для большей эмоциональности текста? Узнаете в этой статье.
Что такое многоточие?
Многоточие – это знак препинания в тексте. В зависимости от языка оно состоит из трех точек (русский, английский) или из шести (китайский). Также многоточие может быть горизонтальным или вертикальным.
Интересно, что многоточия используются не только при письме, но и в математике, к примеру при составлении числовых рядов: 1, 2, 3, 4. 100.
В этом случае многоточие означает, что пропускаются цифры, которые можно вывести логическим путем. Их слишком много для того, чтобы прописывать все, так что на замену ставят несколько точек.
История знака
Нельзя назвать точную дату появления многоточия, что означает его несомненную древность.
Одним из первых случаев употребления этого знака препинания можно считать трактаты Древней Греции. В них многоточие заменяло смысловую часть предложения, которая и так всем была ясна. К примеру, «Не лезь не в свои дела, а то пострадаешь!» могло быть записано как «Не лезь, а то. «
В Греции и Риме многоточия в предложениях означали незавершенность мысли. Так же знак использовался в записях на латыни.
Квинтилианус, один из древних мыслителей, призывал своих соотечественников не злоупотреблять многоточиями, поскольку из-за них предложения сливались в один большой кусок текста, никому не понятный. Этот клич вызвал многие споры: как понять, где «уместно» использовать знак, а где он не нужен? Как правильно использовать многоточие и что означает его переизбыток?
Использовать многоточие в русской литературе стали в восемнадцатом веке с легкой руки Карамзина. Он ввел знак как художественный прием для обогащения текста. В прозе многоточие обозначало эмоциональность и незаконченность мысли.
Спустя время этот знак перешел в обычную жизнь, письма запестрели многоточиями, что означает: знак прижился и «ушел в народ».
Многоточие в литературе
В художественном тексте можно встретить многоточия гораздо чаще, чем в нехудожественной литературе. Дело в том, что многоточия в конце предложения означают незавершенность и незаконченность мысли, чего не могут себе позволить авторы научных статей. Помимо этого, многоточие в литературе может:
И это далеко не все. С восемнадцатого века многоточия прочно вошли в русскую литературу и обрели множество значений. Обычно объяснять смысл этого знака препинания не нужно. Читателю из контекста становится понятно, что означают многоточия в конце предложений.
Правила использования
Существуют некоторые правила в использовании данного знака:
М. В. Ломоносов писал, что «красота, великолепие, сила и богатство российского языка явствует довольно из книг, в прошлые века писаных…».
Что означает многоточие в переписке
Многоточия перешли не только в литературу, но и в повседневную переписку. Если ваш собеседник шлет вам смс с кучей лишних точек, то вам хотят что-то сказать.
Итак, о чем говорит избыток многоточий в переписках:
Когда ставить, а когда нет?
Вы должны интуитивно понимать, когда многоточие уместно, а когда нет. В том же случае, если вы не уверены, стоит ли использовать этот знак, лучше воздержитесь от него.
Помните, знаки препинания – как специи в блюде. Слишком много приправ никому не понравится, всего должно быть в меру!
Здесь легко и интересно общаться. Присоединяйся!
Незаконченная фраза, типа думай сама дальше что я этим хотел тебе сказать.
не представляю современного мужчину, пишущего письмо женщине
три известные всем буквы?
догадайся, мол, сама?)))
что это еще не конец
Сколько у государства не воруй,все равно своего не вернешь
догадайся мол сама
думаю,то же,что и женщины к мужчине:недосказанность
все зависит от смысла оного письма.
продолжение следует,если женщина согласится то она узнает что это за продолжение))
Как понять, что ты ему нравишься? Внимательно посмотри на сообщения, которые он тебе присылает. А опытный психолог поможет разобраться в тонкостях переписки с мужчиной.
Полезные советы от Ярослава Самойлова, которые помогут тебе понять, что ты действительно ему нравишься!
Уверен, ты давно заметила, что СМС и переписка через социальные сети стали частью современного общения.
Вся эта переписка может содержать еще и скрытые подсказки о наших интересах. Во время общения в соц. сетях вполне можно понять, что ты нравишься мужчине.
Признаки, что ты нравишься мужчине, зашифрованные в его сообщениях.
Когда ты научишься извлекать из переписки бессознательно заложенную туда информацию, ты научишься лучше понимать мужчин.
Сейчас я расскажу тебе, как понять, зачем мужчина пишет СМС того или иного содержания. Это подскажет, что ему действительно нужно – твое тело или твоя душа, просто поразвлечься или построить отношения.
Первое, о чем ты должна себя спросить, когда читаешь сообщение от мужчины: «Что он пишет? И зачем он это пишет?». Приведенные ниже примеры помогут с этим разобраться.
Разнообразные позитивные сообщения
Беззаботный текст без особой смысловой нагрузки может означать, что он ищет способ войти с тобой в контакт. Потому что ты ему нравишься.
Вот признаки таких сообщений:
– он использует уменьшительно-ласкательные клички (обычно по названиям зверьков) и варианты твоего имени – котенок, рыбка, Танечка, Настенька и т. д.;
– он всегда быстро отвечает, а когда не может – сообщает об этом (вместо игнорирования и молчания);
– он присылает анекдоты, смешные диалоги и другие вещи, направленные на то, чтобы развеселить тебя;
– пишет, что ты ему снилась;
– присылает слова из песен;
– поднимает темы, которые способны заставить тебя ностальгировать (старый фильм, момент из детства/юношества и т. д.);
– пишет о ком-то или чем-то, что напоминает ему тебя;
– присылает фотки милых котиков.
Серьезные вещи и похвала
Еще один признак, что ты нравишься мужчине – сообщения, в которых он рассказывает о важных событиях из его жизни, обсуждает личные проблемы и всячески показывает свою благосклонность к тебе. Это значит, он ценит твое мнение и доверяет настолько, что может эмоционально раскрываться.
Итак, тебе не составит труда понять, что ты нравишься мужчине, если он:
– в сообщениях делает акцент на твоей пунктуальности, дружелюбности, терпеливости и остальных твоих, казалось бы, обычных качествах;
– часто использует фразы «Я ценю это», «Спасибо», «Скучаю по тебе»;
– делает комплименты касательно твоего внешнего вида, ума, талантов и т. д.;
– предлагает свою помощь, если узнаёт, что она тебе нужна;
– может попросить у тебя помощи в вещах, в которых сам не очень разбирается (ну или сделать вид, что ему нужна такая помощь);
– сообщает о произошедших в его жизни значительных событиях и о его переживаниях по их поводу;
– рассказывает о проблемах на работе, конфликтах с друзьями, попутно спрашивая твоего совета.
Форматирование и длина
Конечно же, в сообщениях тайный смысл кроется не только в словах. Оказывается, смайлики, длина переписки (как по количеству символов, так и по продолжительности) и способ написания слов также дают возможность понять, что ты нравишься мужчине.
Явные признаки этого, что ему нравится общаться с тобой:
– он отвечает на каждое твое сообщение (пускай даже короткими фразами), в итоге выстраивая непрерывную цепочку переписки;
– он часто пишет фразы вроде «Ха-ха» и присылает смайлики;
– использует восклицательные знаки и пишет слова большими буквами, чтобы придать большего значения содержанию своих сообщений;
– ведет с тобой переписку, используя все доступные способы – электронная почта, СМС, Facebook, Вконтакте;
– присылает смешные картинки и видео в соц. сетях, даже когда вы рядом;
– присылает сообщения ЧАСТО;
– пишет сообщения одно за другим, не дожидаясь, пока ты ответишь на предыдущее;
– избегает использования сленговых выражений («ржака») и стандартного «LOL» (старается быть более изобретательным, небанальным);
– не матерится;
– старается писать без ошибок, тщательно разбивая длинные тексты на абзацы.
Когда он пишет?
Иногда время, в которое он присылает сообщения, может сказать больше, чем текст в нем.
Вот несколько советов по расшифровке временных параметров сообщений:
– явный признак, что ты нравишься мужчине – после встречи с тобой он присылает сообщение вроде «Я хорошо провел с тобой время»;
– если он не пишет сообщения с 12 ночи до 7 утра, значит он как минимум тебя уважает, как максимум – сама знаешь;
– сообщений от него в два раза больше, чем от любого другого человека из твоего списка контактов;
– переписка может продолжаться часами;
– он присылает пробное сообщение, в котором интересуется, удобно ли тебе сейчас общаться;
– если он не отвечает на твои сообщения больше чем сутки, значит твои подозрения, что ты ему нравишься, являются лишь подозрениями (хотя, может он уехал на дачу и забыл телефон дома?).
Плоскость, прямая линия, луч
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Обозначение прямой
Например, на рисунке 1 обозначены такие прямые:
Рис. 1 Обозначение прямой линии
Рис. 2 Обозначение прямой с несколькими точками
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
Рис. 5 Пересечение прямых
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
Луч имеет второе название – полупрямая.
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 22
Числовая прямая (или, что то же самое, числовая ось) — понятие нехитрое. Более того, числовая прямая — главный помощник в решении любых заданий с неравенствами! Любых. От примитивных линейных неравенств до сложных показательных или логарифмических неравенств, систем неравенств и метода интервалов. Освоим темку, пока всё просто?)
Что такое числовая прямая? Что такое координатная прямая?
С понятием числовой прямой вы все уже сталкивались, когда изучали такие темы как координаты точек (5-й класс), страшное понятие модуля числа (6-й класс), и особенно когда рисовали графики функций (7-й класс). Вспомним ещё разок?)
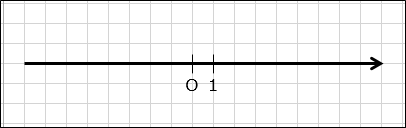
Всё то же самое, ничего нового! Первым делом возьмём и нарисуем в тетрадке самую обычную прямую и дополнительно укажем на ней:
1) Начало отсчёта или начало координат (точку О);
2) Положительное направление (стрелочкой);
3) Масштаб или единицу измерения длины (например, одна тетрадная клетка).
Вот и всё. Про устройство числовой прямой вы тоже давно в курсе (надеюсь). Но на всякий случай напоминаю. Начало координат всегда соответствует числу 0. Все положительные числа изображаются на положительной полуоси справа от нуля, в направлении стрелочки. А все отрицательные — слева от нуля, на отрицательной полуоси. Большее число всегда располагается правее меньшего, а меньшее — левее большего. Элементарно, Ватсон!)
Ну хорошо, прямая и прямая. Но почему — числовая? Ответ очевиден. Каждой точке на прямой соответствует какое-то число. Положительное, отрицательное, целое, дробное, иррациональное — какое угодно. Но — число! Поэтому и прямая — числовая. Это число имеет специальное и вполне научное название — координата точки. Отсюда следует, что числовая прямая — и координатная прямая тоже. Вот так. Два термина в одном флаконе.)
А вот теперь мы с вами колоссально расширяем наши возможности. Начинаем работать с числовой прямой на полную катушку! Готовы?)
Что такое числовой промежуток? Виды числовых промежутков.
В уравнениях было всё просто. Нашли икс, да и записали в ответ. Например, х=2. В неравенствах же ответом обычно служит не одно-два числа, а промежуток. Числовой промежуток. Или даже несколько числовых промежутков. Это и смущает поначалу…) Что это за зверь такой — числовой промежуток?
Числовой промежуток — это просто какой-то кусочек числовой прямой. И всё!
Сейчас начинается самое весёлое. Сейчас мы нашу числовую прямую будем пилить.) Пилить не на дрова, а на… числовые промежутки.)
Вот прям берём числовую прямую и вырезаем из неё какой-то кусочек какими-то точками. Которые, напоминаю, соответствуют каким-то числам. Вот и получаем — числовой промежуток. Разумеется, вырезать конкретный кусочек числовой прямой можно по-разному, да…)
Соответственно, и числовые промежутки в математике бывают разных видов.
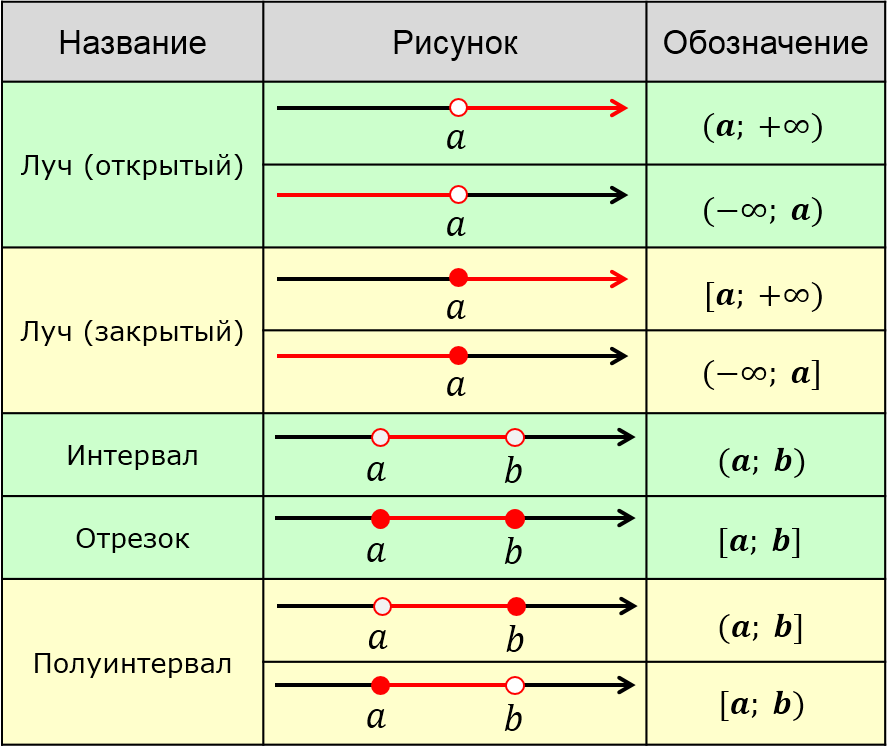
Вот они, эти виды (подкрашены красным цветом):
Смотрим на табличку и… мама родная! Какие-то непонятные кружочки (пустые внутри и закрашенные), какой-то странный иероглиф «∞», да ещё и со знаками плюс/минус, круглые и квадратные скобочки.
Вам и вправду страшно? Возможно… Но сейчас вы увидите, насколько всё просто! Читаем дальше.)
Граничные точки
Я разгадала знак бесконечность… (Земфира)
А может ли числовой промежуток в каком-то направлении быть неограниченным?
А почему — нет? Запросто! Можно распилить числовую прямую не в двух точках, а в какой-то одной точке. И забрать себе одну часть — левую или правую. Бесконечную… Или — луч. Только для обозначения этой бесконечной границы буквы или числа не годятся. Зато есть специальный значок «∞«. Значок этот так и называется — «бесконечность». Очевидно, бесконечность бывает двух видов (точнее, двух знаков) — плюс (+∞) или минус (-∞). В зависимости от того, какой именно луч, какая часть прямой, правая или левая, берётся на дальнейшее рассмотрение.
Кружочки и скобочки…
Граничная точка — это, как и намекает название, точка, задающая границу числового промежутка. Слева или справа. Естественно, у думающих тут же возникает вполне логичный и важный вопрос: А куда относить саму граничную точку? Включать её в состав промежутка или нет?
Именно для ответа на этот вопрос нам и служат всякие кружочки и скобочки в обозначениях и на рисунках!
Запоминаем:
Если граничная точка в числовой промежуток НЕ ВХОДИТ, то на числовой прямой она рисуется НЕЗАКРАШЕННОЙ. Т.е. пустой внутри. В математике такие точки называются выколотыми точками. В обозначениях выколотые точки всегда соседствуют с круглыми скобками «(» или «)».
Если же граничная точка в числовой промежуток ВХОДИТ, то на числовой прямой она рисуется ЗАКРАШЕННОЙ, а в записи обозначается квадратной скобкой «[» или «]».
Вот и вся расшифровка.) Кстати говоря, специальные названия промежутков (луч, отрезок, интервал, полуинтервал) запоминать пока не обязательно. Всё равно поначалу будете путаться. Это для общей эрудиции сделано.) На практике обычно не заморачиваются и говорят «числовой промежуток такой-то…», без уточнения вида — луч, отрезок и т.д. А иногда и совсем кратко — просто «промежуток». Если и вы путаетесь — говорите так же. Не ошибётесь! А спецназвания оставим для старших классов. Но если запомнили (и поняли!) названия промежутков — что ж, только респект!)
Теперь можно потренироваться в записи и чтении числовых промежутков. Чтобы не мычать… Ну что, потренируемся?
Читаем числовые промежутки и рисуем их на оси!
С чтением и рисованием числовых промежутков обычно никаких проблем нет. Нужно только чётко понимать, что означают все эти скобочки и кружочки, что разбирались в предыдущем параграфе.
Например, задан числовой промежуток (0; 5].
Словами эта запись звучит так: числовой промежуток от нуля до пяти, не включая ноль и включая пять.
Читаем (и пишем) именно в таком порядке — от левой границы до правой.
Левая граница (т.е. число 0) соседствует с круглой скобкой «(«, о чём нам и говорят слова «не включая». Этот факт означает, что число 0 в наш промежуток не входит. Например, число 0,1 входит, и даже 0,000001 — ещё входит. Хоть чуть-чуть, да больше нуля. А вот ровно ноль — уже нет…
Пятёрка же — напротив, соседствует с квадратной скобкой «]», что говорит нам о том, что сама она также входит в наш промежуток. И отражено словом «включая» в словесной расшифровке.
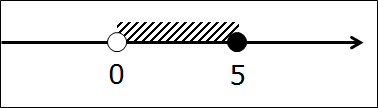
А теперь нарисуем наш промежуток на оси. Для этого рисуем числовую прямую и отмечаем на ней граничные точки 0 и 5.
Заметили разницу между нулём и пятёркой? Ну да, трудно не заметить! 😉 Точка 0 изображена белой, т.е. незакрашенной. Пустой внутри. Или, по-математически, выколотой точкой. Это, как мы с вами уже выяснили, означает, что ноль — не входит в наш промежуток. В отличие от пятёрки, которая входит в промежуток. И на рисунке, соответственно, нарисованной чёрной. Закрашенной.) Я специально точки такими здоровыми изобразил. Чтобы хорошенько врезались в память…
Итак, мы отметили на оси границы промежутка. Осталось лишь отметить все остальные числа, которые входят в этот промежуток. Вы спросите: Как? Ведь между нулём и пятёркой находится бесконечно много чисел! Это и 1, и 2,5, и 3,14, и 4,9999 и так далее… И что? Все-все отмечать)?
Нет, конечно. Всё гораздо проще!) Сейчас мы с вами отметим на прямой все интересующие нас числа одним махом! Тут есть два варианта. Вариант первый — штриховка. Просто берём и подштриховываем весь кусочек прямой между 0 и 5.
Вариант второй рассмотрим на следующем примере.
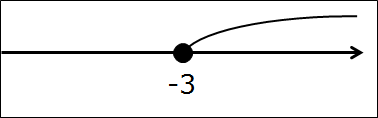
В этот раз дан промежуток такой: [-3; +∞).
Для начала читаем словами название промежутка с гордо поднятой головой: Числовой промежуток от минус трёх до плюс бесконечности, включая минус три!
Вот так. А теперь вопрос на засыпку: почему я оборвал чтение на словах «включая минус три…» и не продолжил мысль гениальными словами «…и не включая плюс бесконечность»?
Всё очень просто. Бесконечность (что плюс, что минус) не может включаться никогда. Это не число, это — символ. Поэтому в подобных записях бесконечность всегда соседствует с круглой скобкой, а в расшифровке говорится просто: «до плюс бесконечности». Или «до минус бесконечности». И всё.
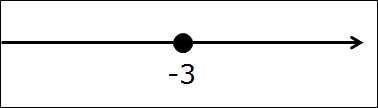
А теперь всё как обычно, рисуем прямую, отмечаем на ней одну единственную точку минус три. Закрашенную, естественно, раз уж скобочка перед минус тройкой — квадратная. Вот так:
И отмечаем все остальные числа, входящие в промежуток от минус тройки до плюс бесконечности. На этот раз я отмечу нужный кусок оси дужкой (от слова дуга) вместо штриховки. Вот так:
Особой разницы между штриховкой и дужками нет. Рисуйте как удобнее. Но в сложных заданиях с неравенствами, где надо постоянно пересекать и объединять много промежутков, дужки предпочтительнее, ибо штриховка куда менее наглядна. Запутаться можно.
Я предпочитаю совмещать оба способа. Получается красиво и наглядно! В следующем уроке, на примерах, сами увидите.)
Вот так рисуются числовые промежутки на оси.
Входит и выходит… ))
А какая нам разница, входит число в указанный промежуток или не входит?
Вопрос смешной. Огромная! Ответ на этот вопрос (входит/не входит) — это ключевой этап в работе с промежутками и с неравенствами вообще! Даже значки специальные придуманы для этого. Вот такие:
За этими странными значками скрываются безобидные слова «принадлежит» и «не принадлежит».
Возьмём, к примеру, промежуток (1; 3].
Входит в этот промежуток, допустим, двойка? Конечно! Раз уж она посерёдке между единичкой и тройкой… А единичка? Э-э-э… Скобка перед ней — круглая! Не входит единичка в наш промежуток. Тройка входит? Попадает на границу, но скобочка — квадратная. Значит, входит! А вот три с половиной — снова не входит. 3,5 строго больше, чем тройка. Выпадает 3,5 из нашего промежутка…
Математически, с помощью значков принадлежности, эти факты можно записать вот так:
А словами можно прочитать вот так:
Два принадлежит промежутку от одного (не включая) до трёх (включая).
Один не принадлежит промежутку от одного (не включая) до трёх (включая).
В этом уроке было простое чтение и рисование промежутков на оси. Пока — цветочки. Переходим к ягодкам. К операциям над числовыми промежутками. Те ещё грабли, да…) Об этом — в следующем уроке.