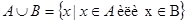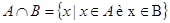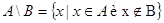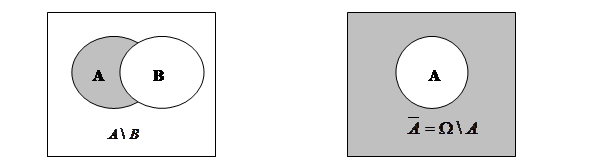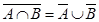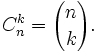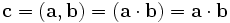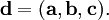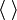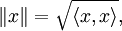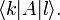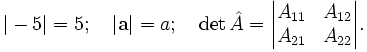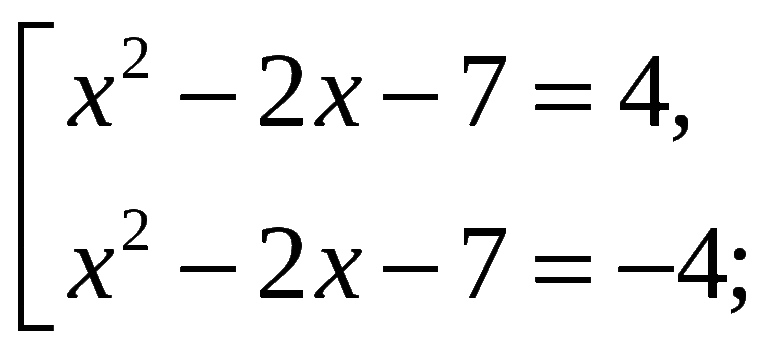Что означают скобки в множествах
Множества
Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N — множество натуральных чисел,
Z — множество целых чисел.
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
Подмножество — это множество, все элементы которого, являются частью другого множества.
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :
Рассмотрим два множества:
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.
При объединении равных множеств объединение будет равно любому из данных множеств:
Скобки в математике
Вы будете перенаправлены на Автор24
Скобки в математике играют очень важную роль: с помощью них задаётся порядок действий с выражением, обозначаются границы промежутков и необходимость выполнения какого-либо действия над выражением. Также с помощью скобок обозначаются вектора и матрицы и действия с множествами.
Использование круглых скобок в математике
Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.
Первое применение.
С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.
В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.
Второе применение.
Третье применение.
Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.
$(x+2)^2; \int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$
Четвёртое применение.
Пятое применение.
Готовые работы на аналогичную тему
Пятое применение.
Квадратные скобки в математике
Что же означают квадратные скобки в математике и для чего они используются?
Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.
Первое применение.
Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.
Второе применение.
Третье применение.
С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.
$\left [ \begin
Фигурная скобка в математике
Первое применение.
С помощью символа фигурной скобки обозначают систему уравнений, решением которой являются корни, подходящие для всех уравнений, включённых в систему.
Второе применение.
Третье применение.
Треугольные скобки
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 03 2021
Операции над множествами



Существуют несколько основных операций над множествами, с помощью которых можно строить новые множества.
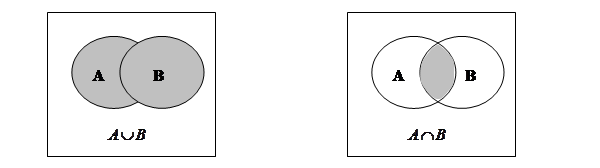
Объединениемдвух множеств А и Вназывается новое множество, содержащее все элементы из А и все элементы из В.
Пересечениемдвух множеств А и Вназывается новое множество, состоящее из тех элементов, которые принадлежат обоим множествам.
Разностьюдвух множеств А и В называется новое множество,содержащее те элементы из А, которые не принадлежат множеству В.
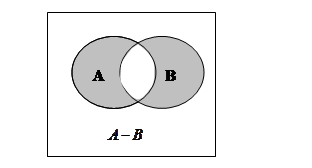
Если класс объектов, на которых определяются различные множества обозначитьU(универсум), то дополнением множестваАназывают разность 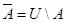
Симметрической разностью множеств А и В называется множество, содержащее все элементы А, не принадлежащие В, и все элементы В, не принадлежащие А.
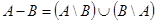
Рисунок 1 – Объединение множеств Рисунок 2 – Пересечение множеств
Рисунок 3 – Разность множеств Рисунок 4 – Дополнение множества
Рисунок 5 – Симметрическая разность множеств
Указанные операции обладают нижеследующими свойствами(законы алгебры множеств).
1. Идемпотентность (удаление одинаковых операндов):
1) 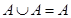
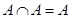
2. Коммутативность (перестановка операндов):
1) 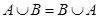
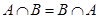
3.Ассоциативность (возможность бесскобочной записи).
1) 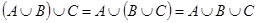
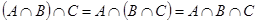
4. Дистрибутивность (раскрытие скобок):
1) 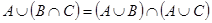
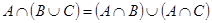
5. Законы (правила) де Моргана:
1) 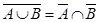
1) 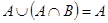
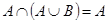
3) 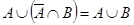
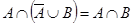
5) 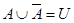
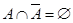
7) 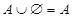
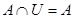
9) 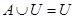
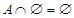
7. Закондвойного отрицания: 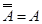
11. 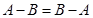
12. 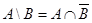
13. 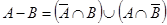
Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств.
Декартовым (прямым) произведением множеств 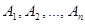
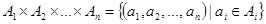
Степенью декартового произведения 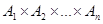
Если все множества 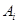
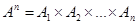
Угловые скобки
Ско́бки — па́рные знаки, используемые в различных областях.
Используются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||.
В математике, физике, химии и др. используются при написании формул.
Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂.
Содержание
Круглые скобки
Используются в математике для задания приоритета математических и логических операций. Например, (2+3)·4 означает, что надо сначала сложить 2 и 3, а затем сумму умножить на 4; аналогично выражение 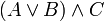
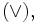
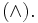
Круглые скобки в математике используются также для выделения аргументов функции: 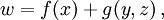
(здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение:
При обозначении диапазона чисел круглые скобки обозначают, что числа, которые находятся по краям множества не включаются в это множество. То есть запись А = (1;3) означает, что в множество включены числа, которые 1(открытый) интервал.
В химических формулах круглые скобки применяются для выделения повторяющихся функциональных групп, например, (NH4)2CO4, Fe2(SO4)3, (C2H5)2O. Также скобки используются в названиях неорганических соединений для обозначения степени окисления элемента, например, хлорид железа(II), гексацианоферрат(III) калия.
Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках.
Во многих языках программирования используются круглые скобки для выделения конструкций. Например, в языках Паскаль и Си в скобках указываются параметры вызова процедур и функций, а в Лиспе — для описания списка.
Квадратные скобки
В лингвистике употребительны для обозначения транскрипции в фонетике или границ составляющих в синтаксисе.
Квадратными скобками в цитатах задают авторский текст, который проясняет контекст цитаты. Например, «Их [заложников] было около 100 человек».
Квадратными скобками в математике могут обозначаться:
В вики-разметке двойные квадратные скобки используются для внутренних ссылок, перенаправлений, категорий и интервики, одинарные — для внешних.
В программировании чаще всего применяются для указания индекса элемента массива.
Часто квадратные скобки используются для обозначения необязательности, например, параметров командной строки (см. подробнее в статье Форма Бэкуса — Наура).
Фигурные скобки
Фигурными скобками в одних математических текстах обозначается операция взятия дробной части, в других — они применяются для обозначения приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок). Фигурные скобки применяют для обозначения множеств. Одинарная фигурная скобка объединяет системы уравнений или неравенств. В математике и классической механике фигурными скобками обозначается оператор специального вида, называемый скобками Пуассона: 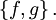
В вики-разметке двойные фигурные скобки применяются для шаблонов.
В программировании фигурные скобки являются или операторными (Си, C++, Perl и комментарием (Паскаль), могут также служить для образования списка (в Сетл).
Угловые скобки
В математике угловыми скобками обозначают кортеж, реже — скалярное произведение в предгильбертовом пространстве, например:
В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как 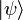
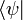
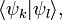
Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например, 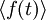
В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте — 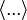
Типографика
В типографике же угловые скобки 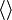
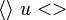
В ТеХе для записи угловых скобок используются команды «\langle» и «\rangle».
ASCII-тексты
В некоторых языках разметки, напр., HTML, XML угловыми скобками выделяют теги.
В вики-разметке также можно использовать HTML-разметку, например комментарии — « », которые видны только при редактировании статьи.
В программировании угловые скобки используются редко, чтобы не создавать путаницы между ними и знаками отношений (« »). Например в Си угловые скобки используются в директиве препроцессора #include вместо кавычек, чтобы показать что включаемый заголовочный файл необходимо искать в одном из стандартных каталогов для заголовочных файлов, например в следующем примере:
файл stdio.h находится в стандартном каталоге, а myheader.h — в текущем каталоге (каталоге исходника программы).
В некоторых текстах, сдвоенные парные « » используются для записи кавычек-ёлочек, например — >.
Косые скобки
Появились на пишущих машинках для экономии клавиш.
В программировании на языке Си косые скобки вместе с дополнительным знаком «*» обозначают начало и конец комментария:
Прямые скобки
Используются в математике для обозначения модуля числа или вектора, определителя матрицы:
Двойные прямые скобки
Используются в математике для обозначения нормы элемента линейного пространства: ||x||; иногда — для матриц:
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
Другие варианты расчета:
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Прочие знаки
Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.
Удобство записи системы уравнений
Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.