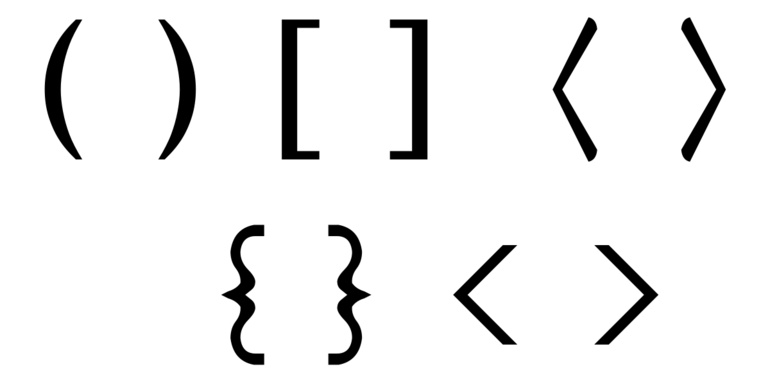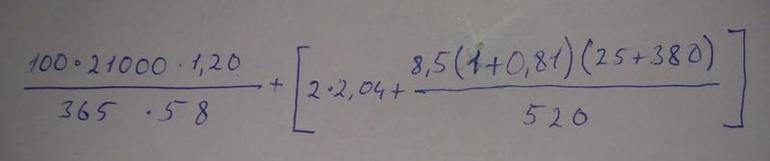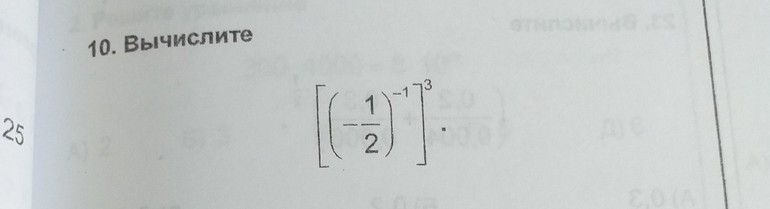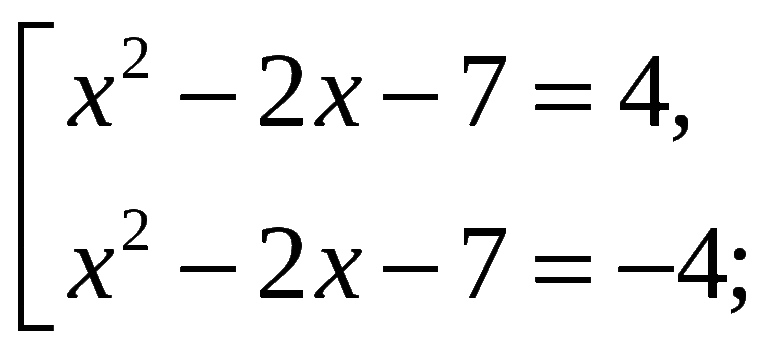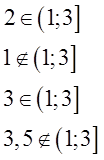Что означают прямые скобки в алгебре 7 класс
Раскрытие скобок: правила и примеры (7 класс)
Правила раскрытия скобок
Если перед скобкой стоит знак плюс, то скобка просто снимается, выражение в ней при этом остается неизменным. Иначе говоря:
Здесь нужно пояснить, что в математике для сокращения записей принято не писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не \(+7+3\), а просто \(7+3\), несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение \((5+x)\) – знайте, что перед скобкой стоит плюс, который не пишут.

Пример. Раскройте скобку и приведите подобные слагаемые: \((x-11)+(2+3x)\).
Решение: \((x-11)+(2+3x)=x-11+2+3x=4x-9\).
Если перед скобкой стоит знак минус, то при снятии скобки каждый член выражения внутри нее меняет знак на противоположный:
Здесь нужно пояснить, что у \(a\), пока оно стояло в скобке, был знак плюс (просто его не писали), и после снятия скобки этот плюс поменялся на минус.
Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).
Решение: \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).
Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть:
Пример. Раскройте скобки \(-2(-3x+5)\).
Решение: Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).
Осталось рассмотреть последнюю ситуацию.
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:
Шаг 2. Раскрываем произведения скобки на множитель как описано выше:
— сначала первое…
Шаг 3. Теперь перемножаем и приводим подобные слагаемые:
Так подробно расписывать все преобразования совсем необязательно, можно сразу перемножать. Но если вы только учитесь раскрывать скобок – пишите подробно, меньше будет шанс ошибиться.
Скобка в скобке
Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).
Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.
При этом важно при раскрытии одной из скобок не трогать все остальное выражение, просто переписывая его как есть.
Давайте для примера разберем написанное выше задание.
Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).
Решение:
Выполнять задание начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относиться – это сама скобка и минус перед ней (выделено зеленым). Всё остальное (не выделенное) переписываем также как было.
Теперь раскрываем вторую скобку, внешнюю.
Упрощаем получившееся выражение…
Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).
Решение:
Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается.
Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке.
Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него.
И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные.
Большая Энциклопедия Нефти и Газа
Прямая скобка
Прямые скобки означают, что так находится только величина силы, но не ее направление. [1]
Прямые скобки означают, что это выражение дает только величину скорости, но не указывает ее направление. [2]
Прямые скобки как символ были предложены математиком К. [3]
Прямые скобки указывают на геометрическую а не алгебраическую разность скоростей. [4]
Прямые скобки с индексом Г внизу обозначают приращение заключенного в скобки выражения при обходе контура по часовой стрелке. Из формулы (10.2.1) следует, что если область многосвязна и главный вектор сил, приложенных к одному из граничных контуров, отличен от нуля, то функции ф или яр, или и та и другая должны быть неоднозначными. Тело, сечение которого представляет собой односвязную область, должно быть в равновесии под действием внешних сил, поэтому, если во внутренних точках не приложены сосредоточенные силы, Л4 Ш2 О и функции ф, я) однозначны. [5]
Прямые скобки означают, что учитывается лишь численное значение ( модуль) векторной величины, стоящей в скобках. [6]
Прямые скобки показывают, что берется арифметическое значение выражения, стоящего в этих скобках. [7]
Прямые скобки в знаменателе ( 41) означают, как обычно, абсолютную величину. [8]
Прямые скобки в уравнении ( 4а) показывают, что берется арифметическое значение величины; двойной знак перед скобками является указанием на одинаковую вероятность как положительных, так и отрицательных средних ошибок. [9]
Прямые скобки показывают, чдо берется арифметическое значение выражения, стоящего в этих скобках. [10]
Двойные прямые скобки обозначают возможность выбора нескольких конструкций. Необходимо использовать по крайней мере одну из конструкций, размещенных одна над другой, и можно использовать более одной констт кции. [11]
Остальные прямые скобки равны нулю. [12]
Здесь двойные прямые скобки означают норму величины, стоящей внутри них. [13]
Прямыми скобками отмечены параметры, которые должны быть приведены на рабочих чертежах червяков и червячных колес. [15]
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
Другие варианты расчета:
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Прочие знаки
Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.
Удобство записи системы уравнений
Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.
Числовая прямая (или, что то же самое, числовая ось) — понятие нехитрое. Более того, числовая прямая — главный помощник в решении любых заданий с неравенствами! Любых. От примитивных линейных неравенств до сложных показательных или логарифмических неравенств, систем неравенств и метода интервалов. Освоим темку, пока всё просто?)
Что такое числовая прямая? Что такое координатная прямая?
С понятием числовой прямой вы все уже сталкивались, когда изучали такие темы как координаты точек (5-й класс), страшное понятие модуля числа (6-й класс), и особенно когда рисовали графики функций (7-й класс). Вспомним ещё разок?)
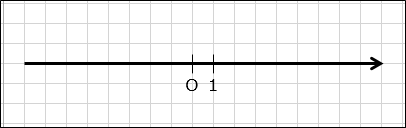
Всё то же самое, ничего нового! Первым делом возьмём и нарисуем в тетрадке самую обычную прямую и дополнительно укажем на ней:
1) Начало отсчёта или начало координат (точку О);
2) Положительное направление (стрелочкой);
3) Масштаб или единицу измерения длины (например, одна тетрадная клетка).
Вот и всё. Про устройство числовой прямой вы тоже давно в курсе (надеюсь). Но на всякий случай напоминаю. Начало координат всегда соответствует числу 0. Все положительные числа изображаются на положительной полуоси справа от нуля, в направлении стрелочки. А все отрицательные — слева от нуля, на отрицательной полуоси. Большее число всегда располагается правее меньшего, а меньшее — левее большего. Элементарно, Ватсон!)
Ну хорошо, прямая и прямая. Но почему — числовая? Ответ очевиден. Каждой точке на прямой соответствует какое-то число. Положительное, отрицательное, целое, дробное, иррациональное — какое угодно. Но — число! Поэтому и прямая — числовая. Это число имеет специальное и вполне научное название — координата точки. Отсюда следует, что числовая прямая — и координатная прямая тоже. Вот так. Два термина в одном флаконе.)
А вот теперь мы с вами колоссально расширяем наши возможности. Начинаем работать с числовой прямой на полную катушку! Готовы?)
Что такое числовой промежуток? Виды числовых промежутков.
В уравнениях было всё просто. Нашли икс, да и записали в ответ. Например, х=2. В неравенствах же ответом обычно служит не одно-два числа, а промежуток. Числовой промежуток. Или даже несколько числовых промежутков. Это и смущает поначалу…) Что это за зверь такой — числовой промежуток?
Числовой промежуток — это просто какой-то кусочек числовой прямой. И всё!
Сейчас начинается самое весёлое. Сейчас мы нашу числовую прямую будем пилить.) Пилить не на дрова, а на… числовые промежутки.)
Вот прям берём числовую прямую и вырезаем из неё какой-то кусочек какими-то точками. Которые, напоминаю, соответствуют каким-то числам. Вот и получаем — числовой промежуток. Разумеется, вырезать конкретный кусочек числовой прямой можно по-разному, да…)
Соответственно, и числовые промежутки в математике бывают разных видов.
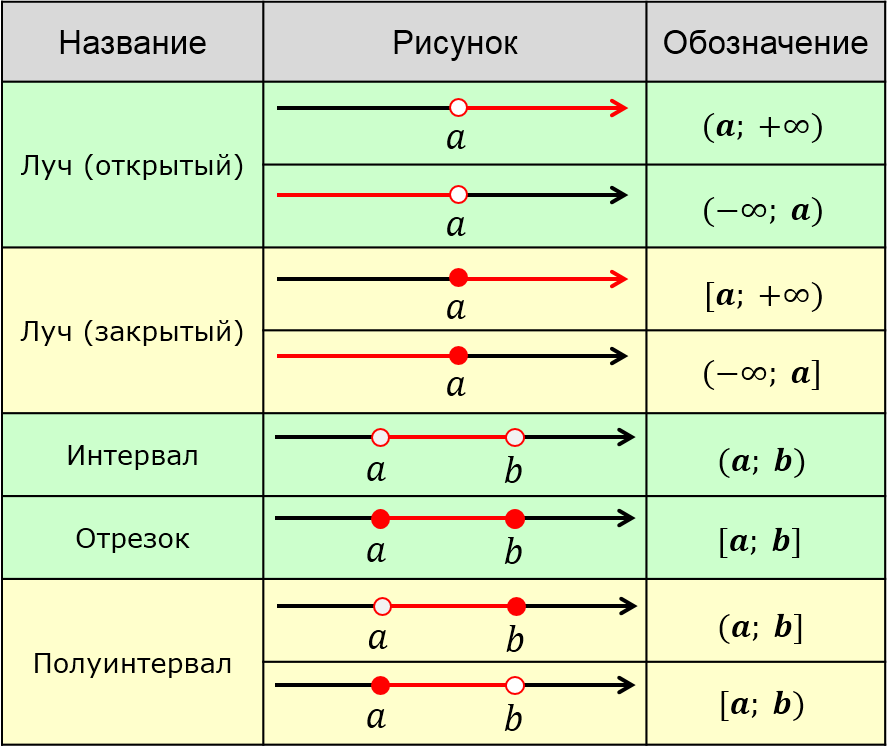
Вот они, эти виды (подкрашены красным цветом):
Смотрим на табличку и… мама родная! Какие-то непонятные кружочки (пустые внутри и закрашенные), какой-то странный иероглиф «∞», да ещё и со знаками плюс/минус, круглые и квадратные скобочки.
Вам и вправду страшно? Возможно… Но сейчас вы увидите, насколько всё просто! Читаем дальше.)
Граничные точки
Я разгадала знак бесконечность… (Земфира)
А может ли числовой промежуток в каком-то направлении быть неограниченным?
А почему — нет? Запросто! Можно распилить числовую прямую не в двух точках, а в какой-то одной точке. И забрать себе одну часть — левую или правую. Бесконечную… Или — луч. Только для обозначения этой бесконечной границы буквы или числа не годятся. Зато есть специальный значок «∞«. Значок этот так и называется — «бесконечность». Очевидно, бесконечность бывает двух видов (точнее, двух знаков) — плюс (+∞) или минус (-∞). В зависимости от того, какой именно луч, какая часть прямой, правая или левая, берётся на дальнейшее рассмотрение.
Кружочки и скобочки…
Граничная точка — это, как и намекает название, точка, задающая границу числового промежутка. Слева или справа. Естественно, у думающих тут же возникает вполне логичный и важный вопрос: А куда относить саму граничную точку? Включать её в состав промежутка или нет?
Именно для ответа на этот вопрос нам и служат всякие кружочки и скобочки в обозначениях и на рисунках!
Запоминаем:
Если граничная точка в числовой промежуток НЕ ВХОДИТ, то на числовой прямой она рисуется НЕЗАКРАШЕННОЙ. Т.е. пустой внутри. В математике такие точки называются выколотыми точками. В обозначениях выколотые точки всегда соседствуют с круглыми скобками «(» или «)».
Если же граничная точка в числовой промежуток ВХОДИТ, то на числовой прямой она рисуется ЗАКРАШЕННОЙ, а в записи обозначается квадратной скобкой «[» или «]».
Вот и вся расшифровка.) Кстати говоря, специальные названия промежутков (луч, отрезок, интервал, полуинтервал) запоминать пока не обязательно. Всё равно поначалу будете путаться. Это для общей эрудиции сделано.) На практике обычно не заморачиваются и говорят «числовой промежуток такой-то…», без уточнения вида — луч, отрезок и т.д. А иногда и совсем кратко — просто «промежуток». Если и вы путаетесь — говорите так же. Не ошибётесь! А спецназвания оставим для старших классов. Но если запомнили (и поняли!) названия промежутков — что ж, только респект!)
Теперь можно потренироваться в записи и чтении числовых промежутков. Чтобы не мычать… Ну что, потренируемся?
Читаем числовые промежутки и рисуем их на оси!
С чтением и рисованием числовых промежутков обычно никаких проблем нет. Нужно только чётко понимать, что означают все эти скобочки и кружочки, что разбирались в предыдущем параграфе.
Например, задан числовой промежуток (0; 5].
Словами эта запись звучит так: числовой промежуток от нуля до пяти, не включая ноль и включая пять.
Читаем (и пишем) именно в таком порядке — от левой границы до правой.
Левая граница (т.е. число 0) соседствует с круглой скобкой «(«, о чём нам и говорят слова «не включая». Этот факт означает, что число 0 в наш промежуток не входит. Например, число 0,1 входит, и даже 0,000001 — ещё входит. Хоть чуть-чуть, да больше нуля. А вот ровно ноль — уже нет…
Пятёрка же — напротив, соседствует с квадратной скобкой «]», что говорит нам о том, что сама она также входит в наш промежуток. И отражено словом «включая» в словесной расшифровке.
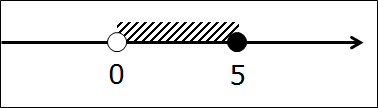
А теперь нарисуем наш промежуток на оси. Для этого рисуем числовую прямую и отмечаем на ней граничные точки 0 и 5.
Заметили разницу между нулём и пятёркой? Ну да, трудно не заметить! 😉 Точка 0 изображена белой, т.е. незакрашенной. Пустой внутри. Или, по-математически, выколотой точкой. Это, как мы с вами уже выяснили, означает, что ноль — не входит в наш промежуток. В отличие от пятёрки, которая входит в промежуток. И на рисунке, соответственно, нарисованной чёрной. Закрашенной.) Я специально точки такими здоровыми изобразил. Чтобы хорошенько врезались в память…
Итак, мы отметили на оси границы промежутка. Осталось лишь отметить все остальные числа, которые входят в этот промежуток. Вы спросите: Как? Ведь между нулём и пятёркой находится бесконечно много чисел! Это и 1, и 2,5, и 3,14, и 4,9999 и так далее… И что? Все-все отмечать)?
Нет, конечно. Всё гораздо проще!) Сейчас мы с вами отметим на прямой все интересующие нас числа одним махом! Тут есть два варианта. Вариант первый — штриховка. Просто берём и подштриховываем весь кусочек прямой между 0 и 5.
Вариант второй рассмотрим на следующем примере.
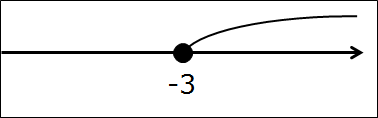
В этот раз дан промежуток такой: [-3; +∞).
Для начала читаем словами название промежутка с гордо поднятой головой: Числовой промежуток от минус трёх до плюс бесконечности, включая минус три!
Вот так. А теперь вопрос на засыпку: почему я оборвал чтение на словах «включая минус три…» и не продолжил мысль гениальными словами «…и не включая плюс бесконечность»?
Всё очень просто. Бесконечность (что плюс, что минус) не может включаться никогда. Это не число, это — символ. Поэтому в подобных записях бесконечность всегда соседствует с круглой скобкой, а в расшифровке говорится просто: «до плюс бесконечности». Или «до минус бесконечности». И всё.
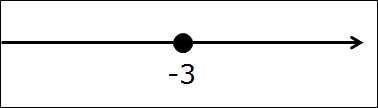
А теперь всё как обычно, рисуем прямую, отмечаем на ней одну единственную точку минус три. Закрашенную, естественно, раз уж скобочка перед минус тройкой — квадратная. Вот так:
И отмечаем все остальные числа, входящие в промежуток от минус тройки до плюс бесконечности. На этот раз я отмечу нужный кусок оси дужкой (от слова дуга) вместо штриховки. Вот так:
Особой разницы между штриховкой и дужками нет. Рисуйте как удобнее. Но в сложных заданиях с неравенствами, где надо постоянно пересекать и объединять много промежутков, дужки предпочтительнее, ибо штриховка куда менее наглядна. Запутаться можно.
Я предпочитаю совмещать оба способа. Получается красиво и наглядно! В следующем уроке, на примерах, сами увидите.)
Вот так рисуются числовые промежутки на оси.
Входит и выходит… ))
А какая нам разница, входит число в указанный промежуток или не входит?
Вопрос смешной. Огромная! Ответ на этот вопрос (входит/не входит) — это ключевой этап в работе с промежутками и с неравенствами вообще! Даже значки специальные придуманы для этого. Вот такие:
За этими странными значками скрываются безобидные слова «принадлежит» и «не принадлежит».
Возьмём, к примеру, промежуток (1; 3].
Входит в этот промежуток, допустим, двойка? Конечно! Раз уж она посерёдке между единичкой и тройкой… А единичка? Э-э-э… Скобка перед ней — круглая! Не входит единичка в наш промежуток. Тройка входит? Попадает на границу, но скобочка — квадратная. Значит, входит! А вот три с половиной — снова не входит. 3,5 строго больше, чем тройка. Выпадает 3,5 из нашего промежутка…
Математически, с помощью значков принадлежности, эти факты можно записать вот так:
А словами можно прочитать вот так:
Два принадлежит промежутку от одного (не включая) до трёх (включая).
Один не принадлежит промежутку от одного (не включая) до трёх (включая).
В этом уроке было простое чтение и рисование промежутков на оси. Пока — цветочки. Переходим к ягодкам. К операциям над числовыми промежутками. Те ещё грабли, да…) Об этом — в следующем уроке.
Прямые скобки
Ско́бки — парные знаки, используемые в различных областях.
Обычно первая в паре скобка называется открывающей, а вторая — закрывающей. Почти всегда (за исключением некоторых математических обозначений) открывающая и закрывающая скобки соответствуют друг другу (квадратная — квадратной и т. д.).
Используются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||.
Используются в математике, физике, химии и других науках для установки приоритета выполнения операции в формулах.
Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂 или 🙂.
Содержание
Круглые (операторные) скобки [ | ]
(здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение:
Круглые скобки в математике используются также для указания бесконечно повторяющегося периода позиционного представления рационального числа, например
При обозначении числовых интервалов круглые скобки обозначают, что числа, которые находятся по краям множества, не включаются в это множество, — интервал является открытым с одной (полусегмент) или обеих сторон. Например,
В химических формулах круглые скобки применяются для выделения повторяющихся функциональных групп, например, (NH4)2CO3, Fe2(SO4)3, (C2H5)2O. Также скобки используются в названиях неорганических соединений для обозначения степени окисления элемента, например, хлорид железа(II), гексацианоферрат(III) калия.
Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках. В русском языке употребляются для выделения пояснительного слова или вставного предложения. Например: Орловская деревня (мы говорим о восточной части Орловской губернии) обыкновенно расположена среди распаханных полей, близ оврага, кое-как превращённого в грязный пруд (И. Тургенев). Непарная закрывающая скобка может использоваться при нумерации пунктов перечисления, например: 1) первый пункт; 2) второй.
Во многих языках программирования используются круглые скобки для выделения конструкций. Например, в языках Паскаль и Си в скобках указываются параметры вызова процедур и функций, а в Лиспе — для описания списка.
Квадратные скобки [ | ]
В лингвистике употребительны для обозначения транскрипции в фонетике или границ составляющих в синтаксисе.
Квадратными скобками в математике могут обозначаться:
В вики-разметке двойные квадратные скобки используются для внутренних ссылок, перенаправлений, категорий и интервики, одинарные — для внешних.
В программировании чаще всего применяются для указания индекса элемента массива, в языке Perl также формируют ссылку на безымянный массив; в Бейсике и некоторых других достаточно старых языках не используются.
В стандарте POSIX определена утилита test, синонимом которой является символ квадратной скобки «[».
Часто квадратные скобки используются для обозначения необязательности, например, параметров командной строки (см. подробнее в статье Форма Бэкуса — Наура).
Фигурные скобки [ | ]
Фигурными скобками в одних математических текстах обозначается операция взятия дробной части, в других — они применяются для обозначения приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок). Фигурные скобки применяют для обозначения множеств. Одинарная фигурная скобка объединяет системы уравнений или неравенств, служит для обозначения кусочно-заданной функции. Как уже было сказано выше, иногда фигурными скобками обозначают антикоммутатор и скобки Пуассона.
В вики-разметке и в некоторых языках разметки веб-шаблонов (Django, Jinja) двойные фигурные скобки <<…>> применяются для шаблонов и встроенных функций и переменных, одинарные в определённых случаях формируют таблицы.
В программировании фигурные скобки являются или операторными (Си, C++, Java, Perl и PHP), или комментарием (Паскаль), могут также служить для образования списка (в Mathematica), анонимного хеш-массива (в Perl, в иных позициях для доступа к элементу хеша), словаря (в Python) или множества (Сетл).
Угловые скобки [ | ]
В математике угловыми скобками обозначают скалярное произведение в предгильбертовом пространстве, например:
Типографика [ | ]
В Τ Ε Χ для записи угловых скобок используются команды «\langle» и «\rangle».
В стандартной пунктуации китайского, японского [ja] и корейского языков используется несколько дополнительных видов скобок, включая шевроны (англ. chevron ), схожие по написанию с угловыми скобками — для горизонтальной 〈 и 〉 или 《 и 》 (в японском языке разрешено использование как знака кавычки 「」) и традиционной вертикальной печати — ︿ и ﹀ или ︽ и ︾. В современной японской печати широко используются скобки европейского образца (), как и арабские цифры. В одном из проектов реформации японского языка даже было предложено [ источник не указан 3172 дня ] ввести европейские скобки вместо традиционных, однако проект был отклонён.
ASCII-тексты [ | ]
В некоторых языках разметки, например HTML, XML, угловыми скобками выделяют теги.
В программировании угловые скобки используются редко, чтобы не создавать путаницы между ними и знаками отношений (« »). Например в Си угловые скобки используются в директиве препроцессора #include вместо кавычек, чтобы показать, что включаемый заголовочный файл необходимо искать в одном из стандартных каталогов для заголовочных файлов, например в следующем примере:
файл stdio.h находится в стандартном каталоге, а myheader.h — в текущем каталоге (каталоге хранения исходного текста программы).
Кроме того, угловые скобки применяются в языках программирования C++, Java и C# при использовании средств обобщённого программирования: шаблонов и дженериков.
В некоторых текстах, сдвоенные парные « » используются для записи кавычек-ёлочек, например — >.
Косые скобки [ | ]
Появились на пишущих машинках для экономии клавиш.
В программировании на языке Си и многих языках с аналогичным синтаксисом косые скобки вместе с дополнительным знаком «*» обозначают начало и конец комментария:
В языке JavaScript косые скобки обозначают регулярное выражение:
Иногда в косых скобках пишут фамилию, расшифровывающую подпись. Например: подпись …. /Иванов И. И./
Прямые скобки [ | ]
Используются в математике для обозначения модуля числа или вектора, определителя матрицы:
Двойные прямые скобки [ | ]
Используются в математике для обозначения нормы элемента линейного пространства: ||x||; иногда — для матриц:
История [ | ]
Круглые скобки появились в 1556 году у Тартальи (для подкоренного выражения) и позднее у Жирара. Одновременно Бомбелли использовал в качестве начальной скобки уголок в виде буквы L, а в качестве конечной — его же в перевёрнутом виде (1550); такая запись стала прародителем квадратных скобок. Фигурные скобки предложил Виет (1593). Всё же большинство математиков тогда предпочитали вместо скобок надчёркивать выделяемое выражение. В общее употребление скобки ввёл Лейбниц.
Поддержка в компьютерах [ | ]
ы Юниа и т. п. закреплены не за левыми и правыми скобками, а за открывающими и закрывающими, поэтому при отображении текста со скобками в режиме «справа налево» каждая скобка меняет своё визуальное направление на противоположное. Так, сочетание ( закреплено за открывающей круглой скобкой, которая выглядит как левая ( в тексте, идущем слева направо, но как правая ) в тексте, идущем справа налево. Однако клавиши на клавиатуре закреплены за левыми и правыми скобками, например клавиша ( закреплена за левой круглой скобкой, которая при наборе текста слева направо является открывающей и получает 40, а справа налево (в раскладках, предназначенных для языков с написанием слов справа налево, например для арабского или иврита) — является закрывающей и получает 41.