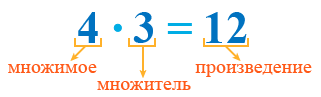Что означают множители в произведении

Умножение натуральных чисел

Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.

Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?

Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.

Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.

Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.

Для записи умножения используется знак х (косой крест) или · (точка), который ставится между числами. Например:

Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак = (равно), после которого записывается полученный результат:

Умножение – это краткая запись сложения одинаковых слагаемых.

Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:

Сократим запись, заменив сложение на умножение:

Оба выражения равны:

6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,

но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.

Множимое, множитель и произведение

Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:

4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.

Произведение — это число, которое получается в результате умножения. Например, в записи:

12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.

Множимое и множитель иначе называются множителями или сомножителями.

Проверка умножения

Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.

Источник

Умножение

В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.

Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24

Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.

Первое число при умножении показывает, какое слагаемое повторяют несколько раз.

Второе число при умножении показывает, сколько раз повторяют это слагаемое.

Результат умножения показывает, какое число получается.

6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24

Числа при умножении

Результат умножения, или Произведение

Чтение числовых выражений

Этот пример можно прочитать по-разному.

Умножение на 1

4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.

23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.

Умножение на 0

8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.

26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.

Умножение на 10

8 • 10 = 80, потому что число 8 повторяют 10 раз.

15 • 10 = 150, потому что число 15 повторяют 10 раз.

Связь деления и умножения

8 • 3 = 24, потому что 8 повторяют 3 раза.

24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.

24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.

В несколько раз больше

Решим задачу:

В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?

Это значит, что котят было 4 раза по 2.

Заменяем сложение умножением и получаем:

Во сколько раз больше? Во сколько раз меньше?

Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?

Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.

Поделись с друзьями в социальных сетях:

Источник

Числа. Произведение чисел. Свойства умножения.

Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой один аргумент складывается столько раз, сколько показывает другой.

Произведение чисел m и n — это сумма n слагаемых, каждое из этих слагаемых = m.

Выражение типа m • n, и значение такого выражения называется произведение чисел m и n. Числа m и n называются множителями.

Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.

Свойства умножения чисел.

1. Коммутативность:

При перестановке множителей местами, значение произведения остается без изменений. Это переместительное свойство умножения.

где, 3 и 4 — множители, а 12 — произведение.

2. Ассоциативность:

В произведении 3-х и больше множителей при перестановке этих множителей либо изменения последовательности выполнения умножения результат остается одинаковым.

3. Дистрибутивность:

4. Произведение всякого натурального числа и единицы, будет соответствовать этому числу.

Произведение всякого натурального числа и нуля, = 0.

Выражения с буквенными множителями записывают так:

Кроме того, не используют знак умножения и перед скобками,

2 • (a + b) записывают как 2(а + b),

Источник

Что такое множитель и разложение на простые множители

Дадим определение понятию «множитель» и разберемся что такое множитель. Какие множители бывают и почему некоторые из множителей — простые.

Определение множителя

В младших классах вы учили, что множители — это числа, которые мы умножаем, называя результат их умножения произведением.

Определения множителя как компонента умножения

Сейчас немного расширим понятие множителя.

Давайте рассмотрим определение множителя на примерах. Давайте определим где в представлении числа или выражения прячется множитель?

Пример 1

Пусть нам дано число 15. Это число можно представить в виде произведения . Значит, согласно определению 5 — это множитель, 3 — это тоже множитель.

Пример 2

Рассмотрим теперь выражение: . Это выражение можно представить в виде произведения . Получаем два множителя — первый множитель (2x-3) и второй множитель (2x+3).

Самое простое произведение имеет два множителя, но может быть и больше множителей.

Простые множители

Пример 1

Разложите число 65 на простые множители.

Решение: число 65 будем делить на простые числа, пока оно нацело не разделится. Так мы видим, что число 65 не делится на 2, 3 и 4, так как не соответствует признакам делимости на эти числа. Зато делится на 5, так как оканчивается на 5. При делении мы получаем 13. Число 13 — простое, так как делится только на себя и на единицу. Таким образом, число . И мы выполнили разложение числа на простые множители. Теперь вы знаете, как разложить число на простые множители.

Пример 2

Разложите число 270 на простые множители.

Решение: Разделим сначала число 270 на 2 (сначала берем самое маленькое простое число), получим 135. Посмотрим, делится ли это число на 3. Для этого сложим все числа, стоящие в разрядах данного числа — . Девять делится на 3, значит, и число 135 разделится на 3: . Получившееся число опять делится на 3: . И снова число 15 делится на 3: . Получили простое число 5. Делим .

Итак, запишем разложение числа 270 на простые множители в виде столбца, где справа от черты мы пишем на какое простое число мы делим, а слева — что получаем:

Разложение числа на простые множители в столбик.

Разложение числа на простые множители в строчку записывается так: .

Про разложение многочлена на множители поговорим в отдельной теме.

Источник

Урок математики во 2-м классе. Тема: «Произведение и множители»

Оборудование: персональный компьютер; мультимедиа-проектор; презентация к уроку (Приложение 1), карточки «Солнышкино задание» для индивидуальной работы; учебник А.Л.Чекин «Математика» 1 часть, 2 класс, издательство «Академкнига/Учебник» 2007г.; тетрадь на печатной основе Е.П.Юдина, О.А.Захарова издательство «Академкнига/ Учебник», 2007 г.

I. Организационный момент

На экране высвечивается 1 слайд.

– Здравствуйте, ребята. В каждом из нас есть маленькое солнце – доброта. Добрый человек – это тот, кто любит людей и помогает им. Добрый человек любит природу и охраняет её, а любовь и помощь согревают, как солнце. Я очень хочу, чтобы урок был для вас действительно добрым и тёплым, принёс много нового и интересного. А вы хотите? Тогда вперёд.

II. Актуализация опорных знаний

На экране высвечивается 2 слайд.

– Откройте тетради и запишите число и название работы.

На экране высвечивается 3 слайд.

– Посмотрите на запись. Что вы можете сказать?

25 – 5 40 – 18
82 + 10 64 + 12
2 · 9 3 · 5

(На экране написаны выражения.)

– Запишите в тетради выражения, распределив на группы.
– На сколько групп вы распределили эти выражения? (Эти выражения мы распределили на три группы.)

Проверка: на экране высвечивается 4 слайд.

– Прочитайте выражения 1 группы. (Мы выписали выражения 25 – 5, 40 – 18)
– Что общего у данных выражений? (Это разности.)
– Прочитайте выражения 2 группы. (Мы выписали выражения 82 + 10, 64 + 12)
– Что общего у данных выражений? (Это суммы.)
– Прочитайте выражения 3группы. (Мы выписали выражения 2 · 9, 3 · 5)
– Что общего у данных выражений? (Это произведения)
– Проверьте. Поднимите руки те, у кого не было ошибок, кто распределил выражения на такие группы. Молодцы!

Продолжение работы по 4 слайду.

– Прочитайте выражения другого цвета разными способами.
– С помощью какого знака обозначено произведение? (Знак в виде точки. По данной программе действие умножения даётся на следующем уроке)
– Можем ли прочитать выражения 3 группы так же как предыдущие? (Нет, ещё не умеем.)
– А хочется ли вам научиться читать эти выражения несколькими способами? (Да)

III. Самоопределение к деятельности. Постановка учебной задачи.

– Прежде чем рассматривать данное выражение, откройте содержание учебника на стр. 5.
– Найдите тему, над которой работали на предыдущем уроке.
– Прочитайте название темы следующей за ней. («Произведение и множители».)

На экране высвечивается пятый слайд с темой урока: «Произведение и множители».

– Поделитесь, над чем, будем работать на уроке? (Будем работать над произведениями, узнаем, что такое множители)
– Какие задачи ставим перед собой? (Проверить свои знания. Посмотреть чему научились. Открыть что-то новое.)

IV. Открытие нового знания

На экране шестой слайд.

– Из всех данных выражений выбери и запиши только произведения.

2 + 3 7 – 5
3 · 4 10 + 1
12 – 2 8 · 12

– Какие выражения выписали? (Мы выписали произведения 3 · 4; 8 ·12)

На этом же слайде проявляются эти выражения

– Какой знак есть в этих выражениях? (Знак в виде точки.)
– Кто догадался, как называются числа, которые образуют произведение? (Множители)
– Прочитайте тему нашего урока ещё раз.

На экране седьмой слайд.

– Как можно прочитать компоненты в выражениях, которые выписали? (Множители 3 и 4, множители 8 и 12.)

– Подтвердим своё предположение с выводом учебника на стр. 93. (Числа, из которых состоит произведение, называются множители. Первое число в произведении это первый множитель, второе число – второй множитель)
– Наше предположение совпало, мы сделали открытие.

На экране восьмой слайд.

– Вернёмся к началу урока. Прочитайте выражение разными способами. (Произведение чисел двух и девяти; первый множитель – 2, второй множитель – 9)

V. Первичное закрепление

Учебник стр. 93 №2 (1 ученик у доски, остальные в тетради).

(Составь и запиши произведение, в котором первый множитель равен 2, второй – 4. Замени это произведение суммой)

– Прочитайте, какое произведение вы записали. (Мы записали 2·4; произведение чисел 2 и 4; первый множитель – 2, второй множитель – 4)

(Запиши сумму в виде произведения. 3+ 3 +3 +3+3+3+3)

– Как вы записали эту сумму в виде произведения. (Мы записали 3 · 7)

Проверка, девятый слайд

– Что обозначает первый множитель этого произведения? (Берём число 3)
– Что показывает второй множитель этого произведения? (Сколько раз берём число 3)

На экране десятый слайд.

Физминутка

Под мелодию песни «Вместе весело шагать…» шагаем, считая в прямом порядке по 2. Прыгаем, считая в обратном порядке по 2. Шагаем, считая в прямом порядке по 3. Прыгаем, считая в обратном порядке по 3.

VI. Самостоятельная работа с самопроверкой по эталону

– Дальше вы будете работать самостоятельно.

Учебник стр. 94 № 4 (Слагаемое 12 повторяется 4 раза. Запиши такую сумму в виде произведения.)

– Прочитайте внимательно задание, постарайтесь выполнить самостоятельно, а на закрытой доске работает 2 ученика.
– Что нужно было выполнить? Проверим работу у доски.
– Кто сомневался? Поставьте знак «?».
– Кто не допустил ошибок? Поставьте «+».
– Назовите первый множитель этого произведения. Что он обозначает?
– Назовите второй множитель этого произведения. Что он обозначает?

VII. Включение в систему знаний и повторение

Проверяем с экрана. Слайды 11, 12, 13.

– Прочитайте 1 ряд задачу, которую было предложено решить.
– Какое решение задачи вы записали?
– Что обозначает первое число в записи произведения? (По 3 тетради). Второе число? (взяли 4 стопки, 4 раза)
Аналогично проверяется 2 и 3 задачи.
– Как называются компоненты в произведении? (Множители)

«Солнышкино задание» по карточкам.

У каждого из вас лежит на парте карточка, это «Солнышкино задание». Прочитайте задание и выполните самостоятельно.
(На карточке задание: запиши суммы, состоящие из одинаковых слагаемых в виде произведения

Проверка «Солнышкино задание» слайд 14.

– Проверьте, так ли у вас получилось?
– У кого всё верно, поставьте «+».
– У кого есть ошибки, поставьте «–».
– У кого были трудности, сомнения?

VIII. Рефлексия деятельности

– Какое открытие для себя вы сегодня сделали? (Узнали, как называются компоненты в произведении, учились читать выражения разными способами. Слайд 15.)
– Какую ставили учебную задачу?
– Удалось её решить?
– Каким способом? (Работой в паре, с помощью учителя, ранее изученного, дружной работой и т.д.)
– Где можно применить эти знания?

– Давайте оценим свою работу. Определите качество успеха. (Слайд 16. Обучающиеся выбирают солнышко по своему настроению от урока: смеётся солнышко – всё было понятно на уроке, всё получилось; грустит солнышко – всё понравилось, но были трудности, надо ещё поработать; грозное солнышко – ничего непонятно, всё было трудно)

– Кто выбрал первое солнышко? Поднимите руки.
– Кто выбрал второе солнышко? Поднимите руки.
– Кто выбрал третье солнышко? Поднимите руки.

IX. Домашнее задание

Высвечивается 17 слайд с домашним заданием.

– Вы подарили мне тепло и радость хорошей работой. Всем за урок спасибо.

Источник