Что означает уровень значимости
4. Уровень значимости
Уровни статистической значимости
Уровень значимости – это вероятность того, что мы сочли различия существенными, в то время как они на самом деле случайны.
Итак, уровень значимости имеет дело с вероятностью.
Уровень значимости показывает степень достоверности выявленных различий между выборками, т.е. показывает, насколько мы можем доверять тому, что различия действительно есть.
Современные научные исследования требуют обязательных расчётов уровня статистической значимости результатов.
Обычно в прикладной статистике используют 3 уровня значимости.
Это 5%-ный уровень значимости. До 5% составляет вероятность того, что мы ошибочно сделали вывод о том, что различия достоверны, в то время как они недостоверны на самом деле. Можно сказать и по-другому: мы лишь на 95% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,95. Общий смысл критерия останется тем же.
Это 1%-ный уровень значимости. Вероятность ошибочного вывода о том, что различия достоверны, составляет не более 1%. Можно сказать и по-другому: мы на 99% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,99. Смысл останется тем же.
Это 0,1%-ный уровень значимости. Всего 0,1% составляет вероятность того, что мы сделали ошибочный вывод о том, что различия достоверны. Это — самый надёжный вариант вывода о достоверности различий. Можно сказать и по-другому: мы на 99,9% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,999. Смысл опять-таки останется тем же.
Уровень значимости – это допустимая ошибка в нашем утверждении, в нашем выводе.
Возможны ошибки двух родов: первого рода ( α ) и второго рода ( β ).
Ошибка I рода – мы отклонили нулевую гипотезу, в то время как она верна.
Вероятность того, что принято правильное решение: 1 – α = 0,95, или 95%.
Уровни значимости для ошибок I рода
1. α ≤ 0,05 – низший уровень
Низший уровень значимости – позволяет отклонять нулевую гипотезу, но еще не разрешает принять альтернативную.
2. α ≤ 0,01 – достаточный уровень
Достаточный уровень – позволяет отклонять нулевую гипотезу и принимать альтернативную.
G – критерий знаков
T – критерий Вилкоксона
U – критерий Манна – Уитни.
Для них обратное соотношение.
3. α ≤ 0,001 – высший уровень значимости.
На практике различия считают достоверными при р ≤ 0,05.
Для ненаправленной статистической гипотезы используется двусторонний критерий значимости. Он более строгий, так как проверяет различия в обе стороны: в сторону нулевой гипотезы и в сторону альтернативной. Поэтому для него используется критерий значимости 0,01.
Мощность критерия – его способность выявлять даже мелкие различия если они есть. Чем мощнее критерий, тем лучше он отвергает нулевую гипотезу и подтверждает альтернативную.
Здесь появляется понятие: ошибка II рода.
Ошибка II рода – это принятие нулевой гипотезы, хотя она не верна.
Мощность критерия: 1 – β
Чем мощнее критерий, тем он привлекательнее для исследователя. Он лучше отвергает нулевую гипотезу.
Чем привлекательны маломощные критерии?
Достоинства маломощных критериев
Широкий диапазон, по отношению к самым разным данным
Применимость к неравным по объему выборкам.
Большая информативность результатов.
Второй по популярности — критерий хи-квадрат, χ 2
Т-критерий Стьюдента – это частный случай дисперсионного анализа для более маленькой по объёму выборки.
Уровень значимости в статистике
Уровень значимости в статистике является важным показателем, отражающим степень уверенности в точности, истинности полученных (прогнозируемых) данных. Понятие широко применяется в различных сферах: от проведения социологических исследований, до статистического тестирования научных гипотез.
Определение
Уровень статистической значимости (или статистически значимый результат) показывает, какова вероятность случайного возникновения исследуемых показателей. Общая статистическая значимость явления выражается коэффициентом р-value (p-уровень). В любом эксперименте или наблюдении существует вероятность, что полученные данные возникли из-за ошибок выборки. Особенно это актуально для социологии.
То есть статистически значимой является величина, чья вероятность случайного возникновения крайне мала либо стремится к крайности. Крайностью в этом контексте считают степень отклонения статистики от нуль-гипотезы (гипотезы, которую проверяют на согласованность с полученными выборочными данными). В научной практике уровень значимости выбирается перед сбором данных и, как правило, его коэффициент составляет 0,05 (5 %). Для систем, где крайне важны точные значения, этот показатель может составлять 0,01 (1 %) и менее.
История вопроса
Понятие уровня значимости было введено британским статистиком и генетиком Рональдом Фишером в 1925 году, когда он разрабатывал методику проверки статистических гипотез. При анализе какого-либо процесса существует определенная вероятность тех либо иных явлений. Трудности возникают при работе с небольшими (либо не очевидными) процентами вероятностей, подпадающими под понятие «погрешность измерений».
При работе со статистическими данными, недостаточно конкретными, чтобы их проверить, ученые сталкивались с проблемой нулевой гипотезы, которая «мешает» оперировать малыми величинами. Фишер предложил для таких систем определить вероятность событий в 5 % (0,05) в качестве удобного выборочного среза, позволяющего отклонить нуль-гипотезу при расчетах.
Введение фиксированного коэффициента
В 1933 году ученые Ежи Нейман и Эгон Пирсон в своих работах рекомендовали заранее (до сбора данных) устанавливать определенный уровень значимости. Примеры использования этих правил хорошо видны во время проведения выборов. Предположим, есть два кандидата, один из которых очень популярен, а второй – малоизвестен. Очевидно, что первый кандидат выборы выиграет, а шансы второго стремятся к нулю. Стремятся – но не равны: всегда есть вероятность форс-мажорных обстоятельств, сенсационной информации, неожиданных решений, которые могут изменить прогнозируемые результаты выборов.
Нейман и Пирсон согласились, что предложенный Фишером уровень значимости 0,05 (обозначаемый символом α) наиболее удобен. Однако сам Фишер в 1956 году выступил против фиксации этого значения. Он считал, что уровень α должен устанавливаться в соответствии с конкретными обстоятельствами. Например, в физике частиц он составляет 0,01.
Значение p-уровня
Термин р-value впервые использован в работах Браунли в 1960 году. P-уровень (p-значение) является показателем, находящимся в обратной зависимости от истинности результатов. Наивысший коэффициент р-value соответствует наименьшему уровню доверия к произведенной выборке зависимости между переменными.
Данное значение отражает вероятность ошибок, связанных с интерпретацией результатов. Предположим, p-уровень = 0,05 (1/20). Он показывает пятипроцентную вероятность того, что найденная в выборке связь между переменными – всего лишь случайная особенность проведенной выборки. То есть, если эта зависимость отсутствует, то при многократных подобных экспериментах в среднем в каждом двадцатом исследовании можно ожидать такую же либо большую зависимость между переменными. Часто p-уровень рассматривается в качестве «допустимой границы» уровня ошибок.
Кстати, р-value может не отражать реальную зависимость между переменными, а лишь показывает некое среднее значение в пределах допущений. В частности, окончательный анализ данных будет также зависеть от выбранных значений данного коэффициента. При p-уровне = 0,05 будут одни результаты, а при коэффициенте, равном 0,01, другие.
Проверка статистических гипотез
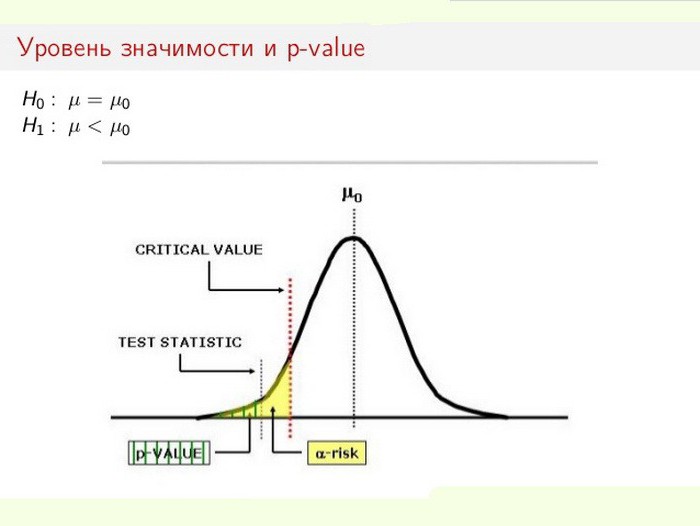
Уровень статистической значимости особенно важен при проверке выдвигаемых гипотез. Например, при расчетах двустороннего теста область отторжения разделяют поровну на обоих концах выборочного распределения (относительно нулевой координаты) и высчитывают истинность полученных данных.
Предположим, при мониторинге некоего процесса (явления) выяснилось, что новая статистическая информация свидетельствует о небольших изменениях относительно предыдущих значений. При этом расхождения в результатах малы, не очевидны, но важны для исследования. Перед специалистом встает дилемма: изменения реально происходят или это ошибки выборки (неточность измерений)?
Эффективность
Необходимо учитывать, что коэффициенты α и р-value не являются точными характеристиками. Каким бы ни был уровень значимости в статистике исследуемого явления, он не является безусловным основанием для принятия гипотезы. Например, чем меньше значение α, тем больше шанс, что устанавливаемая гипотеза значима. Однако существует риск ошибиться, что уменьшает статистическую мощность (значимость) исследования.
Исследователи, которые зацикливаются исключительно на статистически значимых результатах, могут получить ошибочные выводы. При этом перепроверить их работу затруднительно, так как ими применяются допущения (коими фактически и являются значения α и р-value). Поэтому рекомендуется всегда, наряду с вычислением статистической значимости, определять другой показатель – величину статистического эффекта. Величина эффекта – это количественная мера силы эффекта.
Проверка статистических гипотез
п.1. Понятие о статистической гипотезе
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| \(H_0\) | \(H_1\) | ||
| Принятая гипотеза | \(H_0\) | True Negative \(H_0\) принята верно | False Negative \(H_0\) принята неверно Ошибка 2-го рода |
| \(H_1\) | False Positive \(H_0\) отвергнута неверно \(H_1\) принята неверно Ошибка 1-го рода | True Positive \(H_0\) отвергнута верно \(H_1\) принята верно | |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Уровень значимости при проверке гипотезы
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости \(p\) | Решение о гипотезе \(H_0\) | Вывод для гипотезы \(H_1\) |
| \(p\gt 0,1\) | \(H_0\) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| \(0,5\lt p\leq 0,1\) | Истинность \(H_0\) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| \(0,01\lt p\leq 0,05\) | Отклонение \(H_0\), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| \(p\leq 0,01\) | Отклонение \(H_0\), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы \(H_1\).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с \(n\geq 100\) критический уровень снижают до α=0,01.
п.3. Критическая область
Различают 3 вида критических областей
п.4. Простая гипотеза и критерии согласия
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
\(H_0\): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
п.5. Критерий согласия \(X^2\) Пирсона
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| \(m_i\) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| \(f_i-m_i\) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| \(\frac<(f_i-m_i)^2> | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| \(m_i\) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| \(f_i-m_i\) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| \(\frac<(f_i-m_i)^2> | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(p_i\) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: \(X_e^2=36,84\)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для \(X_<кр>^2=X^2(\alpha,k-2)\).
Для уровня значимости α=0,05 и k=8, r=1 находим:
\(X_<кр>^2\approx 12,59\)
Получается, что: \(X_e^2\gt X_<кр>^2\)
Гипотеза \(H_0\) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x= <4;5;6;7>с редким числом попаданий:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 8 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 35 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(p_i\) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: \(X_e^2=1,12\)
Критическое значение статистики ищем в виде \(X_<кр>^2=X^2(\alpha,k-2)\), где α=0,05 и k=5, r=1
\(X_<кр>^2\approx 7,81\)
Получается, что: \(X_e^2\lt X_<кр>^2\)
Гипотеза \(H_0\) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики \(X_e^2\) в Примере 2, основной вклад внесло слагаемое для \(x_i=7\). Оно равно 34,34 и поэтому сумма \(X_e^2=36,84\) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты \(x_i=4,375\) слагаемое статистики равно 0,16 и сумма \(X_e^2=1,12\) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Статистическая значимость
Статистическая значимость часто применяется в маркетинге. С ее помощью определяют правильность выдвинутых предположений и вероятность их результатов. Она позволяет сделать выбор среди представленных теорий, что приводит к получению отличных результатов на практике.
Что такое статистическая значимость
Суть статистической значимости состоит в определении того, существует ли реальное основание в разнице между выбранными для исследования показателями, или это случайность? С данным понятием тесно связаны «нулевая» и «альтернативная» гипотезы.
Для лучшего понимания термина «статистическая значимость» необходимо понять, что такое «проверка гипотез». Эти два термина тесно взаимосвязаны.
Гипотеза иначе называется теорией. После окончания ее разработки требуется установить порядок по сбору достаточного количества доказательств этой теории и собрать их. Существует два типа гипотез: нулевая и альтернативная.
Нулевая гипотеза представляет собой теорию, которая гласит, что внесение коррективов ничего не поменяет, то есть сравниваемые объекты равнозначны в своих свойствах и нет смысла что-либо менять. Суть исследования заключается в опровержении гипотезы.
Альтернативная (исследовательская) гипотеза подразумевает сравнение, в результате которого один объект показывает себя эффективнее, чем другой.
Статистическая значимость как количественный показатель требует оценки. Оценка проходит поэтапно.
Постановка эксперимента
Все начинается с формулировки гипотезы. При этом должно быть выдвижение и нулевой, и альтернативной гипотезы. Придется сравнивать два набора данных для выяснения схожести и отличий. Эти утверждения требуют подтверждения с помощью экспериментальных данных.
Данный уровень представляет собой порог статистической значимости, который каждый устанавливает сам. Этот уровень носит название displaystyle \alpha >\alpha – уровня. Чаще всего, устанавливают значение в 0,05. Вероятность найти разницу составляет 5%. Чем выше уровень, тем достовернее результаты.
Когда нужна максимальная достоверность, стоит снизить значение с 0,05 до 0,01. Чаще всего, такие показатели применяют в производстве для выявления брака. Однако для большинства экспериментов достаточно значения в 0,05.
Решение об используемом критерии
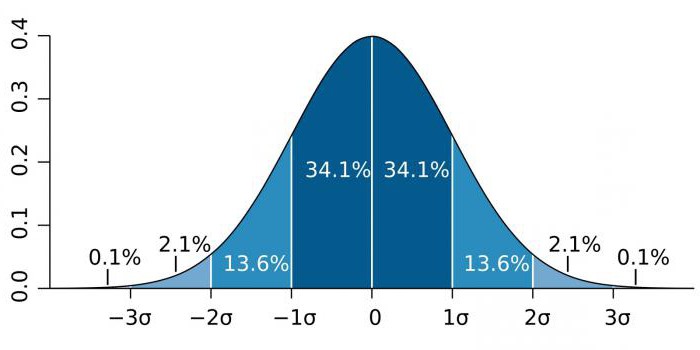
После установки уровня требуется определить, какой критерий использовать: одно- или двусторонний. Здесь стоит опираться на t-критерии Стьюдента. Они показывают, насколько нормально распределены данные. Графически они представлены в виде колоколообразной кривой. Большее количество результатов расположено в середине.
Критерий Стьюдента позволяет математически проверить расположены ли данные в установленных пределах или же выпадают из нормального распределения.
Двусторонний критерий нужен, когда нет уверенности в том, что показатели находятся выше или ниже установленной нормы распределения.
Когда есть точная уверенность, в каком направлении может наблюдаться выход за пределы нормы, нужно использовать односторонний критерий.
Определение объема выборки
Здесь потребуется статистическая мощность. Она представляет собой вероятность, что при выбранном объеме будет получен ожидаемый результат. Распространенный порог — 80%. Для анализа можно использовать специальные онлайн-калькуляторы. Это позволит определить оптимальный объем выборки.
Часто проводят пробное исследование, которое позволяет получить данные для анализа и установить объем выборки. Когда такой возможности нет, стоит поискать в тематической литературе усредненные значения.
Вычисление стандартного отклонения
Стандартное отклонение показывает величину разброса данных. Оно позволяет сделать выбор о близости или отдаленности данных. Их вычисляют по следующей формуле: s = √∑((xi – µ)2/(N – 1)).
s — стандартное отклонение;
∑ указывает на необходимость суммировать полученные данные по выборке;
xi соответствует значению i, то есть отдельному полученному результату;
µ — это среднее значение для данной группы;
N — общее число данных в выборке.
Теперь потребуется отыскать среднее значение для каждой группы. Для этого суммируют средние значения каждой группы и делят на объем выборки.
Далее необходимо определить разницу (xi – µ). Для этого следует вычесть из найденной средней величины каждое полученное значение.
Теперь каждую полученную величину умножают на саму себя или возводят во вторую степень и суммируют величины. После этой операции не должно остаться отрицательных значений.
Следующий шаг — деление объема минус один. Делят полученную в предыдущем шаге сумму на величину, полученную от вычитания единицы. После этого извлекают квадратный корень из величины. Это и будет нужная величина стандартного отклонения.
Определение значимости
Для определения значимости потребуется взять две группы данных. Для последней вычисляют стандартное отклонение, после чего вычисляют дисперсию между обеими группами по формуле:
sd — дисперсия между двумя группами;
s1 — стандартное отклонение в группе 1, N1 — объем выборки в группе 1;
s2 — стандартное отклонение в группе 2, N2 — объем выборки в группе 2.
Необходимо определить t-оценку показателей для перевода полученных данных в стандартизированную форму, которая позволить провести сравнение с другими данными. Эта оценка делает возможным проверку t-критерия, а также выяснение величины отличия одной группы от другой. Для определения t-оценки применяют формулу: t = (µ1 – µ2)/sd:
µ1 — среднее значение для первой группы;
µ2 — среднее значение для второй группы;
sd — дисперсия между двумя выборками.
Совет: первым используют большее среднее значение, чтобы итоговая величина не была отрицательной.
Далее требуется определить степень свободы выборки. Для этого вычисляют объем: суммируют объемы двух выборок и вычитают 2. Полученная величина станет окончательной. Ее оценивают по таблице значений критерия Стьюдента (t-критерия). Таблица представлена ниже.
Пользоваться представленной таблицей просто: находите строку в соответствии с полученной степенью свободы и определяете соответствующее t-оценке Р-значение.
Например, при степени свободы 8 и t-оценке 2,61 Р-значение для одностороннего критерия попадает между 0,01 и 0,025. При выбранном показателе в 0,05 эти данные попадают в категорию «статистически значимые». Это помогает сделать выбор в пользу альтернативной гипотезы и отказаться от нулевой.
Заключение
Определение статистической значимости помогает решать маркетинговые задачи и минимизировать риски. Такие расчеты часто проводятся при A/B тестированиях и помогают узнать, как будет вести себя клиент в будущем, окупится ли товар и т.д.