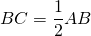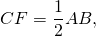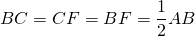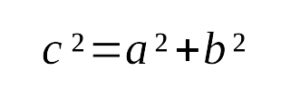Что означает угол 30 градусов в прямоугольном треугольнике

Прямоугольный треугольник

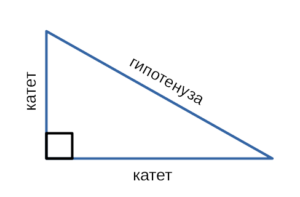
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Признаки равенства прямоугольных треугольников

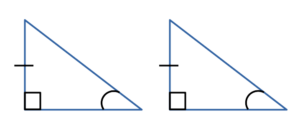
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Источник

Прямоугольные треугольники

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

Площадь прямоугольного треугольника равна половине произведения его катетов

Подставим найденное значение в формулу косинуса

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

Источник

Катет, лежащий против угла 30 градусов

Катет, лежащий против угла 30 градусов, равен половине гипотенузы.

Проведем из вершины прямого угла медиану CF.

Так как медиана, проведенная к гипотенузе, равна половине гипотенузы, то

Так как BF=CF, то треугольник BFC — равнобедренный с основанием BC.

Следовательно, у него углы при основании равны:

Так как сумма углов треугольника равна 180º, то в треугольнике BFC

Поскольку все углы треугольника BFC равны, то этот треугольник — равносторонний.

Значит, все его стороны равны и

Что и требовалось доказать.

Так как сумма острых углов прямоугольного треугольника равна 90º, то

Построим треугольник ADC, равный треугольнику ABC.

В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).

Следовательно, в треугольнике ABD все углы равны:

Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.

Источник

Прямоугольный треугольник: Признаки Равенства и Подобия

Определение

Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

Формулы:

Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

Источник

Технологическая карта «Прямоугольный треугольник. Свойства прямоугольного треугольника. (Прямоугольный треугольник с углом в 30°).»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА

Учебный предмет: Геометрия

Тема урока: Прямоугольный треугольник. Свойства прямоугольного треугольника. (Прямоугольный треугольник с углом в 30 ° ).

Тип урока: открытие новых знаний

Главная дидактическая цель урока: Совершенствовать навыки решения задач на применение свойств прямоугольного треугольника.

Планируемые образовательные результаты:

1)предметные: учащиеся научатся доказывать свойства прямоугольных треугольников и применять их на практике в решении текстовых задач, решать задачи по готовым чертежам. 2)метапредметные:

-коммуникативные УУД: умение работать в парах и группе, обсуждать свойства прямоугольных треугольников;

— познавательные УУД: формировать навыки синтеза и анализа информации, формирование логического мышления, умения работать с информацией;

— личностные УУД: формировать мотивацию, осознание смысла учения и личной ответственности за будущий результат; уметь адекватно реагировать на трудности и не бояться сделать ошибку.

Ресурсы: раздаточный материал, мультимедиа.

Источник